Метод базирующийся на использовании критериев предпочтения
Метод базируется на использовании таблицы состояний объекта, построенной в соответствии с принципами, изложенными в предыдущем параграфе. Причем вся заданная совокупность элементарных проверок {pj} безусловно должна обеспечивать обнаружение и идентификацию каждого возможного состояния объекта. Задача состоит лишь в отборе из этой избыточной совокупности проверок такого подмножества, которое бы обеспечивала при многократном использовании минимальную стоимость тестирования.
При этом средняя стоимость определения состояния объекта должна рассчитываться с учетом вероятностей нахождения объекта в каждом из возможных состояний.
Данный метод ветвей и границ позволяет строить как безусловные, так и условные тесты.
Безусловным называют тест, состоящий из фиксированного количества элементарных проверок при фиксированной их последовательности независимо от действительного состояния объекта.
Условным называют тест, в котором последовательность элементарных проверок зависит от результатов уже выполненных проверок, т.е. определяется действительным состоянием объекта.
При использовании условных тестов (или условных алгоритмов диагностирования) длина теста в каждом конкретном случае будет зависеть от действительного состояния объекта. Поэтому естественным является требование, чтобы наиболее вероятные состояния объекта определялись бы наиболее короткими тестовыми последовательностями.
Выбрав любую проверку из множества {pj} и выполнив ее, можно в зависимости от ее результата, который должен быть дуальным независимо от физической природы измеряемых при выполнении проверки показателей, можно разделить все множество возможных состояний, в которых может находиться объект, на два подмножества: Sj0 и Sj1 одно из которых соответствует нулевому результату j-ой проверки, другое – единичному. Поскольку порядок выполнения следующих проверок для идентификации действительного состояния объекта неизвестен, то вычислить среднюю стоимость определения любого из возможных состояний в каждом из подмножеств невозможно. Однако можно определить нижнюю границу этой стоимости
lim(pj,S)=Cj 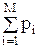 +lim(Sj0)+lim(Sj1) (3.4)
+lim(Sj0)+lim(Sj1) (3.4)
Значения нижней границы стоимости для любой последовательности проверок определяются аналогичными выражениями, например, для последовательности проверок pj, pf, pg нижняя граница стоимости будет
lim(pj,pf,pg,S)=Cj 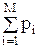 +lim(pf,Sj0)+lim(pg,Sj1) (3.5)
+lim(pf,Sj0)+lim(pg,Sj1) (3.5)
Общий алгоритм поиска оптимального теста состоит в следующем.
На первом шаге рассчитываются нижние границы стоимости при выборе в качестве первой проверки каждой из множества {pj} и выбирается та из них, которая имеет наименьшую нижнюю границу стоимости.
На втором шаге рассчитываются нижние границы всех пар проверок, где в качестве первой взята проверка, выбранная на предыдущем шаге. Из них выбирается та пара, которая имеет наименьшую нижнюю границу стоимости.
На третьем шаге выбирается оптимальная тройка проверок и т.д., пока каждое из получившихся подмножеств состояний в результате всех проведенных проверок будет содержать не более двух состояний объекта.
Рассмотрим применение этого метода на примере.
Пусть диагностируемый объект состоит из четырех элементов. Вероятности отказов каждого из элементов, подсчитанные методами теории надежности, составляют: q1=0.05; q2=0.07; q3=0.03; q4=0.10. Максимальная кратность диагностируемых неисправностей равна двум. Исходное множество элементарных проверок содержит 12 проверок, каждая из которых характеризуется стоимостью, определяемой в относительных единицах, согласно (3.2).
Определим вначале двоичные векторы всех диагностируемых состояний объекта и их вероятности.
Всего должно быть M=n+1+ 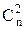 диагностируемых состояний (все состояния с одной и двумя неисправностями плюс одно исправное состояние)
диагностируемых состояний (все состояния с одной и двумя неисправностями плюс одно исправное состояние)
M=4+1+ 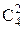 =5+4×3/2=11
=5+4×3/2=11
Их двоичные векторы: 1111, 0111, 1011, 1101, 1110, 0011, 0101, 0110, 1001, 1010, 1100. Вероятности этих состояний будем подсчитывать как вероятности сложных событий, каждое из которых представляет совокупность четырех независимых событий:
Psi=p1×p2×p3×p4,
где p1, p2, p3, p4 – вероятность нахождения каждого из 4-х элементов объекта в исправном или неисправном состоянии, причем вероятности исправных состояний элементов равны pi=1-qi, где qi – заданные вероятности отказов элементов.
Подсчитанные таким образом вероятности состояний объекта сведены в табл. 3.1.
Таблица 3.1
Двоичные векторы состояний и их вероятности
| Si | PSi | Si | PSi | Si | PSi |
| (1111) | 0.7713 | 0.0857 | 0.0018 | ||
| (0111) | 0.0406 | 0.0031 | 0.0061 | ||
| (1011) | 0.0580 | 0.0012 | 0.0026 | ||
| (1101) | 0.0238 | 0.0045 |
В таблице 3.2. представлена исходная таблица состояний объекта, при составлении которой все состояния расположены и пронумерованы в порядке убывания их вероятностей, а проверки расположены и пронумерованы в порядке возрастания их стоимости.
Согласно изложенному выше общему алгоритму построения оптимального теста мы должны на первом шаге брать в качестве первой проверки каждую из 12 и рассчитать нижнюю границу стоимости тестов, которые могут быть построены, если в качестве первой взята именно эта проверка. Однако это требует проведения большой вычислительной работы и возможно лишь с использованием ЭВМ. Для сокращения расчетов при выборе очередности проверок будем руководствоваться следующими соображениями, которые помогут избежать перебора многих комбинаций:
1) для уменьшения средней стоимости тестирования необходимо состояния с наибольшей вероятностью идентифицировать самыми короткими тестами, а с малой – длинными;
2) при одинаковой информативности нескольких проверок, выбираемых на очередном шаге для идентификации определенного состояния объекта, предпочтение следует отдавать проверке с наименьшей стоимостью.
Таблица 3.2.
Таблица состояний объекта
| Si | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | p11 | p12 | PSi |
| S1 (1111) | 0.7713 | ||||||||||||
| S2 (1110) | 0.0857 | ||||||||||||
| S3 (1011) | 0.0580 | ||||||||||||
| S4 (0111) | 0.0406 | ||||||||||||
| S5 (1101) | 0.0238 | ||||||||||||
| S6 (1010) | 0.0061 | ||||||||||||
| S7 (0110) | 0.0045 | ||||||||||||
| S8 (0011) | 0.0031 | ||||||||||||
| S9 (1100) | 0.0026 | ||||||||||||
| S10 (1001) | 0.0018 | ||||||||||||
| S11(0101) | 0.0012 | ||||||||||||
| Cj | 0.9987 | ||||||||||||
| nj |
Таблица 3.3.
Исходная таблица состояний
| Si | S1 (1111) | S2(1110) | S3(1011) | S4(0111) | S5(1101) | S6(1010) | S7(0110) | S8(0011) | S9(1100) | S10(0101) | S1(1001)1 | nj | Cj |
| p1 | 2,2 | ||||||||||||
| p2 | 2,5 | ||||||||||||
| p3 | 2,7 | ||||||||||||
| p4 | 3,1 | ||||||||||||
| p5 | 3,5 | ||||||||||||
| p6 | 3,8 | ||||||||||||
| p7 | 4,3 | ||||||||||||
| p8 | 4,8 | ||||||||||||
| p9 | 5,0 | ||||||||||||
| p10 | 5,4 | ||||||||||||
| p11 | 5,7 | ||||||||||||
| p12 | 6,0 | ||||||||||||
| РSi | 0,7713 | 0,0857 | 0,0580 | 0,0406 | 0,0238 | 0,0061 | 0,0045 | 0,0031 | 0,0026 | 0,0018 | 0,0012 |
Для уменьшения средней длины теста в соответствии с принципом Шеннона необходимо выбирать проверки в такой очередности, чтобы каждая из них разделяла возможные состояния объекта на две группы с примерно равной суммарной вероятностью. Исходя из этого первая проверка должна делить все возможные состояния объекта на две группы с примерно одинаковой вероятностью. В нашем случае вероятность исправного состояния (S1) существенно больше суммы вероятностей всех остальных состояний. Следовательно желательно, чтобы первая проверка отделяла состояние S1 от всех остальных. Поскольку при состоянии S1 все проверки дают 1, наилучшей будет проверка, содержащая максимальное количество нулей, особенно в верхней части таблицы, где расположены наиболее вероятные состояния. Такой проверкой является p4. Кроме состояния S1 она дает 1 только для двух состояний S9 и S11 с малыми вероятностями (0.0026 и 0.0012). Да и стоимость ее не высока (31). Таким образом, не производя расчета нижних границ стоимости тестов для всех остальных проверок, можно с уверенностью считать, что первой проверкой оптимального теста должна быть проверка p4. Она разделяет все возможные состояния объекта на две группы. Единице соответствует группа состояний (S1, S9, S11) с суммарной вероятностью 0.7751. Нулю соответствуют все остальные состояния с суммарной вероятностью 0.2236. Рассчитаем нижнюю границу стоимости теста для данного случая. В соответствии с (3.4)
lim(p4,S)=C4 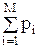 +lim(S40)+lim(S41)=31×0.9987+lim(S40)+lim(S41).
+lim(S40)+lim(S41)=31×0.9987+lim(S40)+lim(S41).
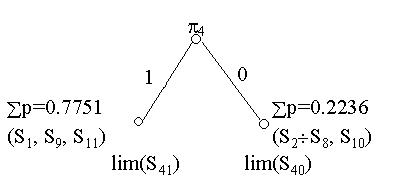 |
Чтобы рассчитать lim(S40) и lim(S41) необходимо построить все возможные деревья решений для дальнейшего разделения этих групп.
Рис. 3.1. Дерево решений после первого шага
Рассмотрим возможные варианты дальнейшего решения. Оптимальное разделения группы состояний (S1, S9, S11) состоит в отделении состояния S1 от двух остальных. Для этого следующая проверка должна давать нули при состояниях S9 и S11. Таких проверок три: p5, p6 и p7. Из них минимальная стоимость у проверки p5. Ее и выбираем. Далее остается лишь разделить состояния S9 и S11, для чего пригодны проверки p1, p2, p9, p10, p11 и p12. Из них, очевидно, надо выбрать проверку p1, как обладающую минимальной стоимостью. Следовательно:
lim(S41)=C5(p1+p9+p11)+C1(p9+p11)=35×0.7751+22×0.0038=27.21
Вторую подгруппу также необходимо разделить на подгруппы с примерно одинаковыми суммарными вероятностями (т.е. вероятность каждой подгруппы должна быть близка к 0.2236/2=0.1118). Здесь возможны два варианта:
1) первая подгруппа образована только одним состоянием S2 ( 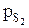 =0.0857), а вторая – всеми остальными (åp=0.1379);
=0.0857), а вторая – всеми остальными (åp=0.1379);
2) первая подгруппа состоит из двух состояний S2 и S3 с суммарной вероятностью 0.1439, а вторая – из всех остальных с суммарной вероятностью 0.0797. Теперь посмотрим на сколько это реализуемо с помощью имеющихся проверок. Рассмотрение таблицы состояний показывает, что ни тот, ни другой вариант не реализуемы. Наиболее близкие к первому варианту дают проверки p3, p7, p8, p10, p11 и p12, а ко второму – p1, p2, p5, p6, p9. Проанализируем их.
Проверка p3 разделяет вторую группу на следующие подгруппы (S2, S5, S8) åp=0.1126, (S3, S4, S6, S7, S10) åp=0.1110.
Проверка p7 разделяет вторую группу на подгруппы: (S2, S6, S7, S8, S10) åp=0.1012 и (S3, S4, S5) åp=0.1224.
Проверка p8 делит на подгруппы: (S2, S4, S6, S10) åp=0.1342 и (S3, S5, S7, S8) åp=0.0894.
Проверка p10 делит на группы: (S2, S4, S5, S6, S7) åp=0.16 и (S3, S8, S10) åp=0.063.
Проверка p11 делит на подгруппы: (S2, S4, S6, S10) åp=0.1342 и (S3, S5, S7, S8) åp=0.0894.
Решения, близкие ко второму варианту, явно будут хуже, т.к. уже сумма вероятностей второго и третьего состояний будет 0.1439, а к ней еще будут добавляться вероятности других состояний. Поэтому их анализировать не будем.
Из рассмотренных вариантов решений наилучшим является решение с выбором в качестве второй проверки p3. Во-первых, она дает разделение второй группы состояний на подгруппы с практически одинаковой вероятностью (0.1126 и 0.1110), а во-вторых, она имеет минимальную стоимость из всех остальных рассмотренных решений. Приняв это решение, получаем
lim(S40)=C3(p2+p3+p4+p5+p6+p7+p8+p10)+lim(S430)+lim(S431).
В итоге дерево решений после второго шага будет иметь вид
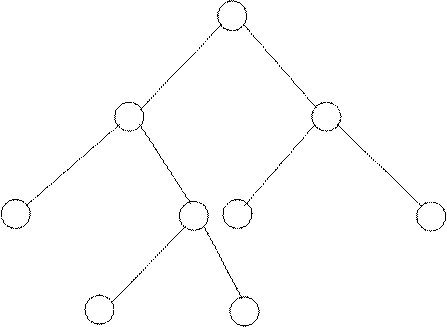
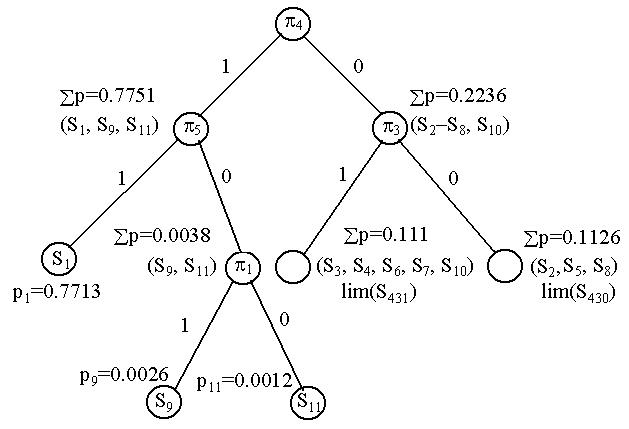
Рис. 3.2. Дерево решений после второго шага.
Правда здесь уже частично (для левой группы состояний) выполнен и третий шаг, который для нее является конечным. Так что нам остается продолжать решение лишь для второй (правой) группы состояний.
Перейдем к рассмотрения третьего шага для правой группы. После второго шага мы получили две подгруппы: (S3, S4, S6, S7, S10) åp=0.111 и (S2, S5, S8) åp=0.1126. Третий шаг должен поделить каждую из них на две части с примерно равными вероятностями (примерно равными 0.055).
Для левой подгруппы желательно отделить S3 (p3=0.058) от всех остальных, причем нельзя использовать проверки p4 и p3, т.к. они уже использованы в этой ветви дерева (проверки p5 и p1 при условном алгоритме использовать можно, т.к. они использовались в других ветвях дерева, при безусловном алгоритме и их использовать было бы нельзя, но мы ориентируемся на условный алгоритм как наиболее экономичный). Такая проверка только одна p9.
С ней могут конкурировать лишь более дешевые проверки, при которых к S3 добавляются маловероятные состояния. Сюда можно отнести проверки p1, при которой к S3 добавляются состояния S6 и S10 и p2, при которой добавляется лишь одно состояние S7. Поэтому следует рассмотреть два варианта: p9 и p2.
При выборе проверки p9 образуются подгруппы (S3) p3=0.058 и (S4, S6, S7, S10) åp=0.053. Причем ее стоимость 50.
При выборе проверки p2 образуются подгруппы (S3, S7) åp=0.0625 и (S4, S6, S10) åp=0.0485, причем ее стоимость 25, т.е. вдвое меньше.
Совершенно очевидно, что более выгодным является второй вариант.
Теперь обратимся к правой группе. Здесь надо искать проверку, отделяющую S2 от состояний S5 и S8.
Это обеспечивают проверки p6, p8 и p11. Выбираем из них самую дешевую p6. В результате от правой группы состояний отделяется состояние S2 с вероятностью p2=0.0857 и остается подгруппа (S5, S8) с суммарной вероятностью åp=0.0269.
В результате после третьего шага мы имеем следующее дерево решений (ограничимся лишь правой ветвью дерева, т.к. левая ветвь уже полностью построена).
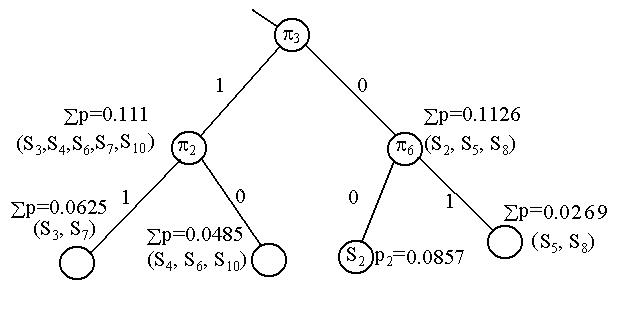
 Рис. 3.3. Дерево решений (правая ветвь) после третьего шага.
Рис. 3.3. Дерево решений (правая ветвь) после третьего шага.
Итак после третьего шага у нас остались три висячих вершины (недостроенных решений): (S3, S7) и (S5, S6) и отделить S4 от (S6, S10), причем для достройки левой ветви дерева (рис. 3.3) нельзя использовать проверки p4, p3 и p2, а для достройки правой ветви – p4, p3 и p6.
Для разделения пары (S3, S7) наиболее дешевой является проверка p1.
Для разделения пары (S5, S8) – тоже проверка p1 (она используется в другой ветви, поэтому ее можно использовать и здесь).
И, наконец, для отделения S4 от (S6, S10) тоже пригодна проверка p1.
Таким образом, на четвертом шаге во всех трех случаях должна выбираться проверка p1.
И, наконец, на пятом шаге остается лишь разделить пару состояний (S6, S10), причем нельзя использовать проверки p4, p3, p2 и p1. Самой дешевой из возможных является проверка p5.
В итоге получается полное дерево решений, отображенное на рис. 3.4.
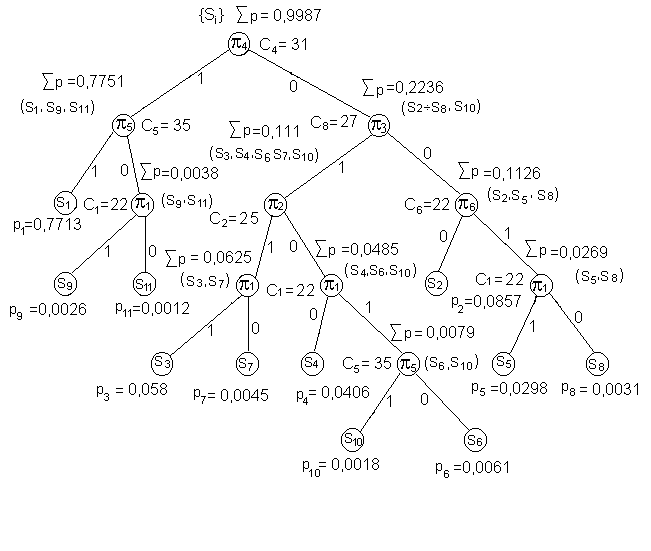
Рис. 3.4. Полное дерево решений условных тестов.
Как видно из рис. 3.4 самый короткий тест, состоящий всего из двух проверок, соответствует самому вероятному состоянию (S1 – исправному состоянию), а самый длинный, состоящий из пяти проверок, состояниям S10 и S6 с суммарной вероятностью 0.0079.
Можно подсчитать среднюю длину теста:
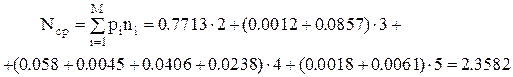
И, наконец, можно определить среднюю стоимость тестирования объекта
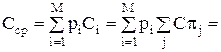 p1(Cp4+Cp5)+(p9+p11)(Cp4+Cp5+Cp1)+
p1(Cp4+Cp5)+(p9+p11)(Cp4+Cp5+Cp1)+
+(Cp4+Cp3+Cp2+Cp1)(p3+p7+p4)+Cp4+Cp3+Cp2+Cp1+Cp5)
(p6+p10)+(Cp4+Cp3+Cp6)p2+(Cp4+Cp3+Cp6+Cp1)(p5+p8)=0.7751×
(31+35)+0.0038×(31+35+22)+(31+27+25+22)×0.0625+(31+27+25+22)×0.0406+(31+27+25+22+35)×0.0079+(31+27+38)×0.0857+
(31+27+38+22)×0.0269=51.157+0.3344+6.5625+4.263+1.106+8.227+3.1742=74.824
Сопоставим эту стоимость со стоимостями всех возможных тестовых последовательностей
С(p4+p5)=31+35=66
С(p4+p5+p1)=31+35+22=88
С(p4+p3+p6)=31+27+38=96
С(p4+p3+p2+p1)=31+27+25+22=105
С(p4+p3+p2+p1+p5)=105+35=140
С(p4+p3+p6+p1)=31+27+38+22=118
Из такого сопоставления следует, что полученный тест по стоимости близок к оптимальному, поскольку средняя стоимость тестирования лишь не на много превышает стоимость самой дешевой тестовой последовательности и меньше стоимости любых других используемых последовательностей.
Опознавателями состояний являются последовательность и результаты произведенных проверок, которые легко определяются из дерева решений:
S1®p4(1)-p5(1); S7®p4(0)-p3(1)-p2(1)-p1(0);
S2®p4(0)-p3(0)-p6(0); S8®p4(0)-p3(0)-p6(1)-p1(0);
S3®p4(0)-p3(1)-p2(1)-p1(1); S9®p4(1)-p5(0)-p1(1);
S4®p4(0)-p3(1)-p2(0)-p1(0); S10®p4(0)-p3(1)-p2(0)-p1(1)-p5(1);
S5®p4(0)-p3(0)-p6(1)-p1(1); S11®p4(1)-p5(0)-p1(0).
S6®p4(0)-p3(1)-p2(0)-p5(0);
Отсюда следует, что основным недостатком условных тестов по сравнению с безусловными является необходимость хранения в памяти ЭВМ всего дерева решений, т.к. оно необходимо для определения очередной проверки (выбор очередной проверки, как видим, зависит от результата предыдущей), и для идентификации действительного состояния объекта (необходимо запоминать не только результаты проверок, но и очередность номеров проверок для определения состояния объекта). Этим усложняется программирование условных тестов и самого тестирования.
Дата добавления: 2017-03-29; просмотров: 658;
