Поиск неисправностей, базирующийся на использовании параметров надежности

Здесь будут рассмотрены такие принципы определения наилучшей последовательности элементарных проверок, которые базируются на использовании таких общих параметров надежности, как безотказность и ремонтопригодность. Суть их состоит в следующем.

Для получения структурной модели объекта используется понятие ремонтопригодности, т.е. объект разбивается по глубине диагностирования до элементов, подлежащих замене при ремонте. А далее для каждого из этих элементов методами теории надежности рассчитываются те или иные параметры безотказности (вероятность безотказной работы, время наработки на отказ и т.д.). Кроме того, при определении наиболее выгодной (по трудоемкости диагностирования) последовательности элементарных проверок может учитываться время, необходимое на проверку каждого элемента. В частности, может быть применен принцип поэлементной проверки объекта, причем очередность проверки элементов определяется комплексным критерием

Q_i=t_i/q_i (3.1)
где t_i – время, необходимое для проверки i-го элемента объекта;

q_i=1-p_i – вероятность отказа i-го элемента (p_i – вероятность безотказной работы i-го элемента).

Для каждого элемента объекта определяется значение критерия Q_i и вначале проверяются элементы с минимальными значениями критерия, а в конце – с максимальными. Поскольку наиболее вероятной является однократная неисправность (неисправен лишь один элемент объекта), то такой алгоритм (в среднем) позволяет отыскать ее за минимальное время.

Однако поэлементная проверка не всегда возможна, т.к. для ее проведения необходимо два условия:

1) доступность входов и выходов каждого элемента;

2) возможность разрыва связей между отдельными элементами.

Более того, даже если эти условия выполняются, то и в этом случае принципу поэлементной проверки присущ ряд недостатков:

1) ввиду разнообразия отдельных элементов для их проверки требуется широкая номенклатура измерительных средств (например, если требуется продиагностировать ЭС глубиной до отдельных компонентов, то элементами оказываются отдельные микросхемы, транзисторы, диоды, резисторы, конденсаторы, индуктивности и для проверки каждого из них нужны свои измерительные средства);

2) для обеспечения доступа к каждому элементу приходится разбирать объект на части (по печатным платам) и каждой платы изготавливать свои адаптеры для доступа к внутриплатным точкам;

3) поэлементная проверка, как правило, требует более длинных тестов, в системных тестах каждая элементарная проверка проверяет несколько элементов, а не один;

4) при поэлементной проверке в большинстве случаев оказываются непроверенными связи между отдельными элементами.

В силу указанных недостатков и ограничений, главным из которых безусловно является необходимость доступа ко всем входам и выходам каждого элемента, поэлементная проверка объекта может быть использована далеко не всегда.

Более общим является алгоритм поиска неисправностей базирующийся на построении таблицы состояний. Причем и этот алгоритм основывается на использовании показателей надежности как одного из критериев поиска. В этом случае для построения алгоритма поиска неисправности используются следующие исходные данные:

1) задано число элементов в объекте n и вероятности отказов каждого элемента q_i;

2) задано конечное пространство возможных проверок {p_j}, из которых набирается тест, и стоимость каждой проверки c_j.

Стоимость проверки c_j определяется в виде

c_j=at_j+bv_j (3.2)

где: a и b – весовые коэффициенты, выбираемые из условий a+b=1 0£a,b£1;

t_j=T_j/minT , v_j=W_j/minW (3.3)

где: T_j – время, необходимое для проведения j-ой проверки; minT – минимальное время проверки – min{p_j}; W_j – денежная стоимость диагностических средств, необходимых для проведения j-ой проверки; minW=minW{p_j} – денежная стоимость минимальной проверки, выбранной из всех N проверок.

При выборе оптимальной совокупности проверок вначале составляется таблица проверок, в которой каждая проверка отображается n-мерным двоичным вектором, где n – число элементов в диагностируемом объекте (согласованные с требуемой глубиной диагностики). Номера элементов объекта образуют столбцы таблицы, а номера проверок – ее строки. Для каждой проверки в клетках таблицы проставляются в тех столбцах, которые данной проверкой не проверяются и единицы в тех столбцах, которые соответствуют элементам, проверяемым настоящей проверкой.

Отсюда следует первое условие, которому должен удовлетворять отобранный тест (совокупность проверок) – каждый столбец в отобранной совокупности проверок должен содержать хотя бы одну единицу.

Однако таких совокупностей проверок, удовлетворяющих данному условию может быть отобрано множество. Следовательно этого условия не достаточно.

Вторым необходимым условием является требование, чтобы каждое диагностируемое состояние объекта, определяемое неисправностью того или иного элемента (или нескольких элементов сразу, если тест должен диагностировать не только одиночные, но и кратные неисправности) могло быть идентифицировано в результате проведения отобранных проверок.

Но и таких тестов может оказаться несколько и среди них надо выбрать наивыгоднейший, который, во-первых, будет состоять из минимального количества проверок, а во-вторых, их совокупность будет иметь минимальную стоимость. Для облегчения поиска такого оптимального теста таблица проверок дополняется справа еще двумя столбцами. В первом из них указывается сколько единиц содержит двоичный вектор каждой проверки, а во втором указывается стоимость каждой проверки, определяемом в соответствии с (3.2).

Полученная таблица используется для построения таблицы состояний. Последняя строится следующим образом.

Первый левый столбец таблицы состояний содержит двоичные векторы возможных состояний объекта, каждому из которых соответствует какая-либо из возможных неисправностей. Для определения числа возможных состояний объекта обычно задаются предельной кратностью неисправностей, которые должен различать данный тест. Очевидно, что если максимальная кратность неисправностей равна 1, то число возможных состояний M=n+1, где n – число элементов объекта (т.к. при этом возможно лишь n неисправных состояний плюс одно состояние, соответствующее исправному объекту). Если максимальная кратность неисправностей равна двум, то M=n+ 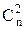+1, где 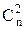– число сочетаний из n по 2 и т.д. В предельном случае, если максимальная кратность неисправностей равна n, число состояний M= .

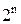Верхняя строка таблицы представляет собой номера элементарных проверок (p_j), j=1, 2, ..., N. В клетках таблицы представляется 1 или 0 в зависимости от того, обнаруживает ли данная проверка данную неисправность (данное состояние) или нет.

Крайний правый столбец содержит вероятности данных состояний, определяемые как p_k=1-q_k, где q_k – вероятность данной неисправности, которая рассчитывается по заданным вероятностям отказа каждого элемента, причем, если k-я неисправность имеет кратность l>1, то q_k=q_a×q_b×...×q_l, где q_a, q_b, ..., q_l – одиночные неисправности, из которых состоит k-я неисправность или k-е состояние объекта.

Обычно все строки (состояния) располагают в порядке убывания их вероятностей. Поскольку вероятность отказа любого элемента много меньше, чем вероятность его исправного состояния (т.е. q_i«0.5), то очевидно, что наиболее вероятным будет исправное состояние объекта, далее будут следовать состояния, соответствующие однократным неисправностям, затем – двукратным и т.д. Если вероятности отказов разных элементов не одинаковы, то очевидно, что будут различаться и вероятности состояний, соответствующих однократным неисправностям но с разными отказавшими элементами. То же относится и к состояниям, соответствующим кратным неисправностям.

При поиске оптимального теста должны учитываться следующие требования:

1) тест должен не только обнаруживать, но и различать все возможные состояния объекта;

2) тест должен состоять из минимально возможного или близкого к нему количества элементарных проверок;

3) стоимость проведения теста (включая стоимость необходимого тестового оборудования) должна быть минимальной или близкой к нему;

4) очередность проверок теста должна соответствовать вероятности определяемых ими состояний объекта.

Строгих формальных методов построения оптимального теста, удовлетворяющего всем указанным требованиям не существует. Поэтому на практике используются различные стратегии и методы построения близких к оптимальным тестов, некоторые из которых будут рассмотрены в дальнейшем.