Построение таблицы покрытий
Эти методы, так же как и методы, основанные на построении таблицы состояний, пригодны и для аналоговых и для цифровых объектов при условии дуальности результатов каждой элементарной проверки, из которых состоит тест. Это означает, что для любого состояния объекта результат любой элементарной проверки может быть либо положительным (отображается единицей), либо отрицательным (отображается нулем). Но в таблице покрытий указываются не сами состояния, а все возможные пары состояний. Если данная проверка различает данную пару состояний (т.е. для одного состояния она дает 0, а для другого 1 или наоборот), то в соответствующей клетке таблицы проставляется 1, а если она не различает эту пару состояний, то проставляется 0 (т.е. в этом случае и для того, и для другого состояния результат данной проверки будет одинаков – либо 0, либо 1 для обоих состояний этой пары). Естественно. Что число возможных пар состояний гораздо больше, чем число самих состояний (оно равно 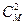 , то есть числу сочетаний из М по 2, где М – число возможных состояний объекта). Следовательно, таблица покрытий является более громоздкой, чем таблица состояний. Однако этот недостаток компенсируется тем, что, во-первых, таблица покрытий допускает чисто формальные преобразования позволяющие ее минимизировать, во-вторых таблица покрытий позволяет аналитическую запись ее содержания в виде булевых соотношений преобразовывать методами булевой алгебры, получая все возможные тесты , включая минимальные, и, в-третьих, таблица покрытий существенно облегчает расчёт нижних границ теста при использовании метода ветвей и границ. С появлением же быстродействующих ЭВМ с огромным объёмом памяти громоздкость таблицы покрытий перестала быть существенным ограничивающим фактором к её применению для синтеза оптимальных тестов.
, то есть числу сочетаний из М по 2, где М – число возможных состояний объекта). Следовательно, таблица покрытий является более громоздкой, чем таблица состояний. Однако этот недостаток компенсируется тем, что, во-первых, таблица покрытий допускает чисто формальные преобразования позволяющие ее минимизировать, во-вторых таблица покрытий позволяет аналитическую запись ее содержания в виде булевых соотношений преобразовывать методами булевой алгебры, получая все возможные тесты , включая минимальные, и, в-третьих, таблица покрытий существенно облегчает расчёт нижних границ теста при использовании метода ветвей и границ. С появлением же быстродействующих ЭВМ с огромным объёмом памяти громоздкость таблицы покрытий перестала быть существенным ограничивающим фактором к её применению для синтеза оптимальных тестов.
Рассмотрим построение таблицы покрытий на том же примере, но для сохранения наглядности таблицы ограничимся лишь диагностикой наиболее вероятных однократных неисправностей (поскольку число пар состояний при 11 возможных состояниях составит 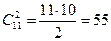 ). Сохранив ту же нумерацию состояний, что в табл. 3.2, получим сокращённую таблицу состояний (табл. 3.12) по которой будем строить таблицу покрытий.3.2, получим сокращённую таблицу состояний (табл.3.12), по которой будем строить таблицу покрытий.
). Сохранив ту же нумерацию состояний, что в табл. 3.2, получим сокращённую таблицу состояний (табл. 3.12) по которой будем строить таблицу покрытий.3.2, получим сокращённую таблицу состояний (табл.3.12), по которой будем строить таблицу покрытий.
Таблица 3.12
Таблица состояний объекта
| {Si} | Psi | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | p9 | p10 | p11 | p12 |
| S1(1111) S2(1110) S3(1011) S4(0111) S5(1101) | 0,7713 0,0857 0,0580 0,0406 0,0238 | ||||||||||||
| Cj | Sp=0,9794 |
Дата добавления: 2017-03-29; просмотров: 1555;
