Получение тестов путём булевых преобразований

Таблицы покрытий

Таблицу покрытий можно записать в аналитическом виде. Рассматривая любой l-й столбец таблицы покрытий (где l=1,2,3...,L – номера столбцов, представляющие собой все возможные пары состояний объекта), можно записать условие, состоящее в том, что для различений данной (1-й) пары состояний достаточно любой одной элементарной проверки, которая имеет в данном столбце единицу, в виде дизъюнкции двоичной переменной, отображающей результаты элементарных проверок:

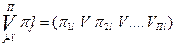(3.5)

Условие достаточности таблицы покрытий, заключающееся в том, что все возможные пары состояний различаются данной совокупностью элементарных проверок, можно представить в виде конъюнкции дизъюнкций вида (3.5), записанных для каждого столбца таблицы покрытий:

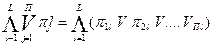(3.6)

Здесь j=1,2,...,П - номера элементарных проверок.

Выражение (3.6) представляет собой логическое произведение логических сумм двоичной переменной p_jl, значения которой и представлены в таблице покрытий. Таким образом, это выражение и представляет собой аналитическую форму записи таблицы покрытий. Для краткости её называют формой ПС или ПS (произведение сумм).

С учётом правил логической алгебры форма ПС может быть преобразована в форму СП (сумм произведений). Для этого достаточно раскрыть скобки в выражении (3.6), т.е. произвести логическое перемножение логических сумм, представленных в скобках.

В результате такого перемножения каждое из слагаемых формы СП будет представлять собой совокупность элементарных проверок, достаточную для различения любой пары возможных состояний объекта. Таким образом, каждое слагаемое формы СП представляет собой тест, позволяющий различать все возможные пары состояний объекта и потому его называют покрытием таблицы покрытий. Причём эти слагаемые могут содержать различное число элементарных проверок, а их совокупность, представленная формой СП, есть все возможные тесты, которые можно получить из данной таблицы покрытий. Очевидно, что среди них будут и минимальный тест, содержащий минимально возможное число элементарных проверок, и максимальный тест, содержащий все элементарные проверки, представленные в исходной таблице покрытий. При этом мы получаем безусловные тесты с безусловной остановкой. Но поскольку форма СП представляет собой все возможные тесты, которые можно получить из исходной таблицы покрытий, то из них можно выбрать оптимальный тест не только по длине (т.е. по количеству элементарных проверок, входящих в него), но и по любым другим критериям, в том числе и по стоимости тестирования, если заданы стоимости каждой элементарной проверки (и они различны). Соответственно, учитывая вероятности различных состояний объекта, из них можно выбрать и оптимальный безусловный тест с условной остановкой и оптимальный условный тест. Для этого достаточно проанализировать каждое из полученных слагаемых формы СП с позиций принятых критериев оптимальности и исходных данных по стоимостям отдельных элементарных проверок и вероятностям всех возможных состояний объекта.

Таким образом, аналитический метод синтеза диагностических тестов является наиболее универсальным и всеобъемлющим и его единственный недостаток состоит в громоздкости вычислений, поскольку для реальных объектов, включая сюда и электронные средства, таблица покрытий может содержать сотни тысяч столбцов, для покрытия которых необходимы миллионы элементарных проверок.

Даже для рассматриваемого нами простейшего примера, в котором диагностируемый объект может иметь всего пять состояний, а исходная таблица покрытий включает в себя лишь 10 элементарных проверок (см. табл.3.13), преобразование формы ПС в форму СП получается достаточно громоздким.

В соответствии с таблицей покрытий, представленной табл.3.13, форма ПС будет иметь вид:

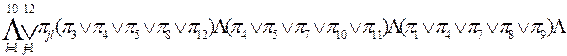
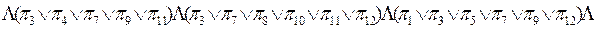
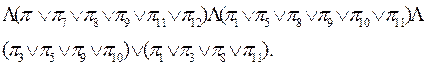
Используя правила логического умножения булевой алгебры произведём перемножение содержащихся в скобках дизъюнкций для получения формы СП, для упрощения записи заменяя знаки V и Ù знаками + и *.

Однако даже для нашего простого примера провести эту работу вручную невозможно, т.к. получаемый при раскрытии скобок многочлен (без учёта упрощений и приведении подобных членов) должен содержать 5*5*5*5*6*6*6*6*4*4 = =12 960 000 членов. Однако реально все возможные решения и не нужны. Оптимальное решение должно находиться среди решений близких к минимальным. Поэтому на следующем шаге (при перемножении многочленов, состоящих из по парных логических произведений двух элементарных проверок) будем отбрасывать все члены, содержащие 4 элементарных проверки, что существенно уменьшит число членов получаемых многочленов.

+p₃p₉p₁₁+p₅p₉p₁₁+p₇p₉p₁₁+p₇p₉p₁₁+p₃p₉p₁₁+p₇p₉p₁₁+p₈p₉p₁₁+

+p₉p₁₀p₁₁+p₉p₁₁+p₉p₁₁p₁₂+p₉p₁₁p₁₂+p₉p₁₁p₁₂+p₁p₉p₁₂+p₃p₉p₁₂+

+p₃p₉p₁₂+p₅p₉p₁₂+p₇p₉p₁₂+p₇p₉p₁₂+p₃p₉p₁₂+p₇p₉p₁₂+p₈p₉p₁₂+

+p₉p₁₀p₁₂+p₉p₁₁p₁₂+p₉p₁₂+p₈p₉p₁₂+p₉p₁₀p₁₂+p₉p₁₁p₁₂+p₉p₁₂+

+p₁p₅p₁₀+p₃p₅p₁₀+p₃p₅p₁₀+p₃p₅p₁₀+p₅p₇p₁₀+p₅p₈p₁₀+p₅p₁₀+

+p₅p₁₀p₁₁+p₅p₁₀p₁₂+p₅p₇p₁₀+p₅p₇p₁₀+p₅p₉p₁₀+p₅p₁₀p₁₂+p₅p₁₀p₁₂+

+p₁p₇p₁₂+p₃p₇p₁₀+p₅p₇p₁₀+p₇p₁₀+p₇p₈p₁₀+p₇p₁₀+p₇p₁₀p₁₁+

+p₇p₁₀p₁₂+p₇p₉p₁₀+p₁p₈p₁₀+p₃p₈p₁₀+p₅p₈p₁₀+p₇p₈p₁₀+p₈p₉p₁₀+

+p₈p₁₀p₁₂+p₁p₉p₁₀+p₃p₉p₁₀+p₅p₉p₁₀+p₇p₉p₁₀+p₈p₉p₁₀+p₉p₁₀+

+p₉p₁₀p₁₁+p₉p₁₀p₁₂+p₁p₁₀p₁₁+p₃p₁₀p₁₁+p₅p₁₀p₁₁+p₇p₁₀p₁₁+

+p₉p₁₀p₁₁+p₁₀p₁₁p₁₂+p₁p₁₀p₁₂+p₃p₁₀p₁₂+p₅p₁₀p₁₂+p₇p₁₀p₁₂+

+p₉p₁₀p₁₂+p₈p₁₀p₁₂+p₁₀p₁₁p₁₂+p₁₀p₁₂+p₁p₇p₁₁+p₃p₇p₁₁+p₅p₇p₁₁+

+p₇p₁₁+p₇p₈p₁₁+p₇p₁₀p₁₁+p₇p₁₁p₁₂+p₇p₉p₁₁+p₇p₁₁p₁₂+p₁p₃p₁₁+

+p₁p₇p₁₁+p₁p₈p₁₁+p₁p₁₀p₁₁+p₁p₁₁+p₁p₁₁p₁₂+p₃p₁₁+p₃p₇p₁₁+

+p₃p₇p₁₁+p₃p₁₀p₁₁+p₃p₁₁+p₃p₁₁p₁₂+p₃p₅p₁₁+p₅p₇p₁₁+p₅p₈p₁₁+

+p₅p₁₀p₁₁+p₅p₁₁+p₅p₁₁p₁₂+p₇p₁₁+p₇p₈p₁₁+p₇p₁₀p₁₁+p₇p₁₁+

+p₇p₁₁p₁₂+p₃p₉p₁₁+p₇p₉p₁₁+p₉p₁₀p₁₁+p₉p₁₁+p₉p₁₁p₁₂+p₈p₁₁p₁₂+

+p₁₀p₁₁p₁₂+p₁₁p₁₂+p₁p₁₁p₁₂+p₃p₁₁p₁₂+p₅p₁₁p₁₂+p₇p₁₁p₁₂+p₉p₁₁p₁₂++p₈p₁₁p₁₂+p₁₀p₁₁p₁₂+p₁₁p₁₂)*(p₁p₃+p₁p₅+p₁p₉+p₁p₁₀+p₃+p₃p₅+

+p₃p₉+p₃p₁₀+p₃p₈+p₅p₈+p₈p₉+p₈p₁₀+p₃p₁₁+p₅p₁₁+p₉p₁₁+p₁₀p₁₁)=

=(p₁p₃p₄+p₁p₃p₅+p₁p₃p₇+p₁p₃p₁₁+p₁p₄p₉+p₁p₄p₈+p₁p₄p₁₂++p₁p₄p₇+p₁p₄p₁₀+p₁p₄p₁₁+p₁p₅p₇+p₁p₇p₈+p₁p₇p₁₂+p₁p₅p₁₁+

+p₁p₈p₁₁+p₁p₁₁p₁₂+p₃p₄+p₃p₄p₅+p₃p₄p₈+p₃p₄p₁₂+p₃p₄p₇+p₃p₄p₁₀++p₃p₄p₁₁+p₃p₅p₇+p₃p₇+p₃p₇p₈+p₃p₇p₁₂+p₃p₇p₁₀+p₃p₇p₁₁+p₃p₅p₈+

+p₃p₈p₁₀+p₃p₈p₁₁+p₃p₄p₉+p₃p₅p₉+p₃p₇p₉+p₃p₉p₁₁+p₄+p₄p₅+p₄p₈++p₄p₁₂+p₄p₅p₈+p₄p₅p₁₂+p₄p₇+p₄p₅p₇+p₄p₇p₈+p₄p₇p₁₂+p₄p₁₀+

+p₄p₅p₁₀+p₄p₈p₁₀+p₄p₁₀p₁₂+p₄p₁₁+p₄p₅p₁₁+p₄p₈p₁₁+p₄p₁₁p₁₂+

+p₄p₇p₁₀+p₄p₇p₁₁+p₄p₈p₁₂+p₄p₉+p₄p₅p₉+p₄p₈p₉+p₄p₉p₁₂+p₄p₇p₉+

+p₄p₉p₁₀+p₄p₉p₁₁+p₄p₇p₁₁+p₄p₇p₈+p₄p₉p₁₂+p₄p₇p₉+p₄p₉p₁₀+

+p₄p₉p₁₁+p₄p₇p₁₁+p₄p₇p₈+p₄p₁₀p₁₁+p₅p₇+p₅p₇p₈+p₅p₇p₁₂+p₅p₇p₁₀++p₅p₇p₁₁+p₅p₇p₉+p₅p₈p₉+p₅p₉+p₅p₉p₁₂+p₅p₉p₁₀+p₇p₈+p₇p₁₂+

+p₇p₈p₁₀+p₇p₁₀p₁₂+p₇p₈p₁₁+p₇p₁₁p₁₂+p₇p₈p₁₂+p₇p₈p₉+p₇p₉p₁₂+

+p₈p₉p₁₀+p₈p₉p₁₁+p₈p₁₀p₁₁+p₈p₁₁+p₈p₁₁p₁₂+p₉p₁₀p₁₂+p₉p₁₁p₁₂)*

* (p₁p₃p₅+p₁p₃p₇+p₁p₃p₈+p₁p₃p₉+p₁p₃p₁₁+p₁p₃p₁₂+p₁p₅p₇+

+p₁p₅p₈+p₁p₅p₁₀++p₁p₅p₁₁₁+p₁p₅p₁₂+p₁p₇+p₁p₇p₈+p₁p₇p₁₀+

+p₁p₇p₁₁+p₁p₇p₁₂+p₁p₇p₉+p₁p₈+p₁p₈p₉+p₁p₈p₁₀+p₁p₈p₁₁+p₁p₈p₁₂++p₁p₉p₁₁+p₁p₉p₁₂+p₁p₉p₁₀+p₁p₁₀p₁₁+p₁p₁₁+p₁p₁₁p₁₂+p₁p₁₂+

+p₁p₁₀p₁₂+p₃p₅+p₃p₅p₇+p₃p₅p₈+p₃p₅p₉+p₃p₅p₁₀+p₃p₅p₁₁+p₃p₅p₁₂++p₃p₇p₈+p₃p₇p₉+p₃p₇p₁₂+p₃p₉p₁₂+p₃p₈p₁₀+p₃p₈p₁₁+p₃p₈p₁₂+

+p₃p₉p₁₀+p₃p₈p₁₁+p₃p₉+p₃p₇p₁₀+p₃p₁₀p₁₁+p₃p₁₀p₁₂+p₃p₈+p₃p₁₁p₁₂++p₅p₇+p₅p₈+p₅p₁₀+p₅p₁₁+p₅p₁₂+p₅p₇p₈+p₃p₈p₉+p₅p₇p₉+p₅p₇p₁₀+

+p₅p₇p₁₁+p₅p₇p₁₂+p₅p₈p₉+p₅p₈p₁₀+p₅p₈p₁₁+p₅p₈p₁₂+p₅p₉p₁₀+

+p₅p₉p₁₁+p₅p₉p₁₂+p₅p₁₀p₁₁+p₅p₁₀p₁₂+p₅p₁₁p₁₂+p₇p₈+p₇p₈p₉+

+p₇p₈p₁₀+p₇p₈p₁₁+p₇p₉+p₇p₈p₁₂+p₈p₉+p₈p₉p₁₀+p₈p₉p₁₁+p₈p₉p₁₂+

+p₈p₁₂+p₈p₁₀p₁₂+p₈p₁₁p₁₂+p₇p₉p₁₀+p₇p₉p₁₁+p₇p₉p₁₂+p₉p₁₀+p₉p₁₁+

+p₉p₁₂+p₉p₁₀p₁₂+p₉p₁₁p₁₂+p₉p₁₀p₁₁+p₃p₇p₁₀+p₇p₁₀+p₇p₁₀p₁₁+

+p₇p₁₀p₁₂+p₁₀p₁₁p₁₂+p₁₀p₁₂+p₇p₁₁p₁₂+p₃p₁₁+p₇p₁₁+p₁₁p₁₂)*(p₁p₃+

+p₁p₅+p₁p₉+p₁p₁₀+p₃+p₃p₅+p₃p₈+p₃p₉+p₃p₁₀+p₃p₁₁+p₅p₈+p₅p₁₁++p₈p₉+p₈p₁₀+p₉p₁₁+p₁₀p₁₁).

Перемножить эти многочлены полностью вручную также невозможно, т.к. при этом мы должны получить многочлен с 156 240 слагаемыми. Поэтому, учитывая, что нас интересуют лишь тесты близкие к минимальным, при перемножении двух первых многочленов будем оставлять лишь двух- и трёхзначные члены, а все остальные отбрасывать:

Спmin=(p₅p₇+p₇p₈+p₁p₃p₅+p₁p₃p₇+p₁p₃p₁₁+p₁p₅p₇+p₁p₇p₈+

+p₁p₇p₁₂+p₁p₅p₁₁+p₁p₈p₁₁+p₁p₁₁p₁₂+p₃p₄p₅+p₃p₄p₉+p₃p₄p₈+

+p₃p₅p₇+p₃p₇p₈+p₃p₇p₉+p₃p₇p₁₀+p₃p₇p₁₁+p₃p₇p₁₂+p₃p₅p₈+

+p₃p₈p₁₀+p₃p₈p₁₁+p₃p₅p₉+p₃p₉p₁₁+p₅p₇p₈+p₅p₇p₉+p₅p₇p₁₀+

+p₅p₇p₁₁+p₅p₇p₁₂+p₅p₈p₉+p₅p₈p₁₁+p₅p₉p₁₀+p₅p₉p₁₂+p₅p₉p₁₁+

+p₇p₈p₉+p₇p₈p₁₁+p₇p₈p₁₂+p₇p₈p₁₀+p₇p₁₀p₁₂+p₇p₁₁p₁₂+p₇p₉p₁₂+

+p₈p₉p₁₀+p₈p₉p₁₁+p₈p₁₁p₁₂+p₈p₁₁+p₉p₁₀p₁₂+p₉p₁₁p₁₂+p₁p₄p₁₁+

+p₁p₄p₁₂+p₄p₅p₇+p₄p₅p₈+p₄p₅p₁₀+p₄p₅p₁₁+p₄p₅p₁₂+p₄p₇p₈+

+p₄p₇p₉+p₄p₈p₉+p₄p₈p₁₂+p₄p₉p₁₀+p₄p₉p₁₁+p₄p₉p₁₂+p₄p₇p₁₀+

+p₄p₁₀p₁₂+p₃p₄p₁₁+p₄p₇p₁₁+p₄p₁₁p₁₂+p₁p₄p₇+p₁p₄p₈+p₁p₄p₁₁+

+p₁p₈p₁₁+p₁p₄p₁₂+p₃p₅p₈+p₃p₉p₁₁+p₃p₄p₉+p₃p₅p₉)*(p₁p₃+p₁p₅+

+p₁p₉+p₁p₁₀p₃+p₃p₅+p₃p₈+p₃p₉+p₃p₁₀+p₃p₁₁+p₅p₈+p₅p₁₁+p₈p₉+

+p₈p₁₀+p₉p₁₁+p₁₀p₁₁).

При перемножении двух оставшихся многочленов ограничимся членами с числом переменных не более четырёх. В итоге получим:

СПmin=p₁p₃p₅p₇+p₁p₃p₇p₈+p₁p₃p₅ +p₁p₃p₇+p₁p₃p₁₁+p₁p₃p₅p₇+

+p₁p₃p₇p₈+p₁p₃p₇p₁₂+p₁p₃p₅p₁₁+p₁p₃p₈p₁₁+p₁p₃p₁₁p₁₂+p₁p₃p₄p₅+

+p₁p₃p₄p₉+p₁p₃p₄p₈+p₁p₃p₅p₇+p₁p₃p₇p₈+p₁p₃p₇p₉+p₁p₃p₇p₁₀+

+p₁p₃p₇p₁₁+p₁p₃p₇p₁₂+p₁p₃p₅p₈+p₁p₃p₈p₁₀+p₁p₃p₈p₁₁+p₁p₃p₅p₉+

+p₁p₃p₉p₁₁+p₁p₃p₄p₁₁+p₁p₃p₄p₁₂+p₁p₃p₄p₇+p₁p₃p₄p₈+p₁p₃p₄p₁₁+

+p₁p₃p₈p₁₁+p₁p₃p₅p₈+p₁p₃p₉p₁₁+p₁p₃p₄p₉+p₁p₃p₅p₉+p₁p₅p₇+

+p₁p₃p₇p₈+p₁p₃p₅+p₁p₃p₅p₇+p₁p₃p₅p₁₁+p₁p₅p₇+p₁p₅p₇p₈+

+p₁p₅p₇p₁₂+p₁p₅p₁₁+p₁p₅p₈p₁₁+p₁p₅p₁₁p₁₂+p₁p₃p₄p₅+p₁p₃p₅p₇+

+p₁p₃p₅p₈+p₁p₃p₅p₉+p₁p₅p₇p₈+p₁p₅p₇p₉+p₁p₅p₇p₁₀+p₁p₅p₇p₁₁+

+p₁p₅p₇p₁₂+p₁p₅p₈p₉+p₁p₅p₈p₁₁+p₁p₅p₉p₁₀+p₁p₅p₉p₁₂+p₁p₅p₉p₁₁+

+p₁p₄p₅p₁₂+p₁p₄p₅p₇+p₁p₄p₅p₈+p₁p₄p₅p₁₀+p₁p₄p₅p₁₁+p₁p₄p₅p₁₂+

+p₁p₄p₅p₇+p₁p₄p₅p₈+p₁p₄p₅p₁₁+p₁p₅p₈p₁₁+p₁p₄p₅p₁₂+p₁p₃p₅p₈+

+p₁p₃p₅p₉+p₁p₅p₇p₉+p₁p₇p₃p₉+p₁p₃p₅p₉+p₁p₃p₇p₉+p₁p₃p₉p₁₁

+p₁p₅p₇p₉+p₁p₇p₈p₉+p₁p₇p₉p₁₂+p₁p₅p₉p₁₁+p₁p₈p₉p₁₁+p₁p₉p₁₁p₁₂+

+p₁p₃p₄p₉+p₁p₃p₇p₉+p₁p₃p₅p₉+p₁p₃p₉p₁₁+p₁p₅p₇p₉+p₁p₅p₈p₉+

+p₁p₅p₉p₁₀+p₁p₅p₉p₁₁+p₁p₅p₉p₁₂+p₁p₇p₈p₉+p₁p₇p₉p₁₂+p₁p₈p₉p₁₀+

+p₁p₈p₉p₁₁+p₁p₉p₁₀p₁₂+p₁p₉p₁₁p₁₂+p₁p₄p₉p₁₁+p₁p₄p₉p₁₂+p₁p₄p₇p₉++p₁p₄p₈p₉+p₁p₄p₉p₁₀+p₁p₄p₉p₁₁+p₁p₄p₉p₁₂+p₁p₄p₇p₉+p₁p₄p₈p₉+

+p₁p₄p₉p₁₁+p₁p₈p₉p₁₁+p₁p₄p₉p₁₂+p₁p₃p₄p₉+p₁p₃p₅p₉+p₁p₃p₇p₁₀+

+p₁p₇p₈p₁₀+p₁p₃p₅p₁₀+p₁p₃p₇p₁₀+p₁p₃p₁₀p₁₁+p₁p₅p₇p₁₀+p₁p₇p₈p₁₀++p₁p₇p₁₀p₁₂+p₁p₅p₁₀p₁₁+p₁p₈p₁₀p₁₁+p₁p₁₀p₁₁p₁₂+p₁p₃p₇p₁₀+

+p₁p₅p₉p₁₀+p₁p₈p₁₀p₁₁+p₁p₉p₁₀p₁₂+p₁p₄p₁₀p₁₁+p₁p₄p₁₀p₁₂+

+p₁p₄p₅p₁₀+p₁p₄p₉p₁₀+p₁p₄p₇p₁₀+p₁p₄p₁₀p₁₂+p₁p₄p₇p₁₀+p₁p₄p₈p₁₀+

+p₁p₄p₁₀p₁₁+p₁p₈p₁₀p₁₁+p₁p₄p₁₀p₁₂+p₃p₅p₇+p₃p₇p₈+p₁p₃p₅+

+p₁p₃p₇+p₁p₃p₁₁+p₁p₃p₅p₇+p₁p₃p₇p₈+p₁p₃p₇p₁₂+p₁p₃p₅p₁₁+

+p₁p₃p₈p₁₁+p₁p₃p₁₁p₁₂+p₃p₄p₅+p₃p₄p₉+p₃p₄p₈+p₃p₅p₇+p₃p₇p₈+

+p₃p₇p₉+p₃p₇p₁₀₁+p₃p₇p₁₁+p₃p₇p₁₂+p₃p₅p₈+p₃p₈p₁₀+p₃p₈p₁₁+

+p₃p₅p₉+p₃p₉p₁₁+p₃p₅p₇p₈+p₃p₅p₇p₉+p₃p₅p₇p₁₀+p₃p₅p₇p₁₁+

+p₃p₅p₇p₁₂+p₃p₅p₈p₉+p₃p₅p₈p₁₁+p₃p₅p₉p₁₀+p₃p₅p₉p₁₂+p₃p₅p₉p₁₁+

+p₃p₇p₈p₉+p₃p₇p₈p₁₁+p₃p₇p₈p₁₂+p₃p₇p₈p₁₀+p₃p₇p₁₀p₁₂+p₃p₇p₁₁p₁₂++p₃p₇p₉p₁₂+p₃p₈p₉p₁₀+p₃p₈p₉p₁₁+p₃p₈p₁₁p₁₂+p₃p₈p₁₁+p₃p₉p₁₀p₁₂+

+p₃p₉p₁₁p₁₂+p₁p₃p₄p₁₁+p₁p₃p₄p₁₂+p₃p₄p₅p₇+p₃p₄p₅p₈+p₃p₄p₅p₁₀+

+p₃p₄p₅p₁₁+p₃p₄p₅p₁₂+p₃p₄p₇p₈+p₃p₄p₇p₉+p₃p₄p₈p₉+p₃p₄p₈p₁₂+

+p₃p₄p₉p₁₀+p₃p₄p₉p₁₁+p₃p₄p₉p₁₂+p₃p₄p₇p₁₀+p₃p₄p₁₀p₁₂+p₃p₄p₁₁+

+p₃p₄p₇p₁₁+p₃p₄p₁₁p₁₂+p₁p₃p₄p₇+p₁p₃p₄p₈+p₁p₃p₄p₁₁+p₁p₃p₈p₁₁+

+p₁p₃p₄p₁₂+p₃p₅p₈+p₃p₉p₁₁+p₃p₄p₉+p₃p₅p₉+p₃p₅p₇+p₃p₅p₇p₈+

+p₁p₃p₅+p₁p₃p₅p₇+p₁p₃p₅p₁₁+p₁p₃p₅p₇+p₁p₃p₅p₁₁+p₃p₄p₅+

+p₃p₄p₅p₉+p₃p₄p₅p₈+p₃p₅p₇+p₃p₅p₇p₈+p₃p₅p₇p₉+p₃p₅p₇p₁₀+

+p₃p₅p₇p₁₁+p₃p₅p₇p₁₂+p₃p₅p₈+p₃p₅p₈p₁₀+p₃p₅p₈p₁₁+p₃p₅p₉+

+p₃p₅p₉p₁₁+p₃p₅p₇p₈+p₃p₅p₇p₉+p₃p₅p₇p₁₀+p₃p₅p₇p₁₁+p₃p₅p₇p₁₂+

+p₃p₅p₈p₉+p₃p₅p₈p₁₁+p₃p₅p₉p₁₀+p₃p₅p₉p₁₂+p₃p₅p₉p₁₁+p₃p₄p₅p₇+

+p₃p₄p₅p₈+p₃p₄p₅p₁₀+p₃p₄p₅p₁₁+p₃p₄p₅p₁₂+p₃p₅p₈+p₃p₅p₉p₁₁+

+p₃p₄p₅p₉+p₃p₅p₉+p₃p₇p₈+p₁p₃p₅p₈+p₁p₃p₇p₈+p₁p₃p₈p₁₁+

+p₃p₄p₅p₈+p₃p₄p₈p₉+p₃p₄p₈+p₃p₅p₇p₈+p₃p₇p₈+p₃p₇p₈p₉+

+p₃p₇p₈p₁₀+p₃p₇p₈p₁₁+p₃p₇p₈p₁₂+p₃p₅p₈+p₃p₈p₁₀+p₃p₈p₇₁+

+p₃p₅p₈p₉+p₃p₈p₉p₁₁+p₃p₅p₇p₈+p₃p₅p₈p₁₁+p₃p₇p₈p₉+p₃p₇p₈p₁₁+

+p₃p₇p₈p₁₂+p₃p₇p₈p₁₀+p₃p₈p₉p₁₀+p₃p₈p₉p₁₁+p₃p₈p₁₁p₁₂+p₃p₈p₁₁+

+p₃p₄p₅p₈+p₃p₄p₇p₈+p₃p₄p₈p₉+p₃p₄p₈p₁₂+p₃p₄p₈p₁₁+p₁p₃p₄p₈+

+p₁p₃p₈p₁₁+p₃p₅p₈+p₃p₈p₉p₁₁+p₃p₄p₈p₉+p₃p₅p₈p₉+p₃p₅p₇p₉+

+p₃p₇p₈p₉+p₁p₃p₅p₉+p₁p₃p₇p₉+p₁p₃p₉p₁₁+p₃p₄p₅p₉+p₃p₄p₉+

+p₃p₄p₈p₉+p₃p₅p₇p₉+p₃p₇p₈p₉+p₃p₇p₉+p₃p₇p₉p₁₀+p₃p₇p₉p₁₁+

+p₃p₅p₉p₁₂+p₃p₅p₈p₉+p₃p₈p₉p₁₀+p₃p₈p₉p₁₁+p₃p₅p₉+p₃p₉p₁₁+

+p₃p₅p₇p₉+p₃p₅p₈p₉+p₃p₅p₉p₁₀+p₃p₅p₉p₁₂+p₃p₅p₉p₁₁+p₃p₇p₈p₉+

+p₃p₇p₉p₁₂+p₃p₈p₉p₁₀+p₃p₈p₉p₁₁+p₃p₉p₁₀p₁₂+p₃p₉p₁₁p₁₂+

+p₃p₄p₈p₉+p₃p₄p₉p₁₀+p₃p₄p₉p₁₁+p₃p₄p₉p₁₂+p₃p₄p₉p₁₁+p₃p₅p₈p₉+

+p₃p₉p₁₁+p₃p₄p₉+p₃p₅p₉+p₃p₅p₇p₁₀+p₃p₇p₈p₁₀+p₁p₃p₅p₁₀+

+p₁p₃p₈p₁₀+p₁p₃p₁₀p₁₁+p₃p₄p₅p₁₀+p₃p₄p₉p₁₀+p₃p₄p₈p₁₀+p₃p₅p₇p₁₀++p₃p₇p₈p₁₀+p₃p₇p₉p₁₀+p₃p₇p₁₀+p₃p₇p₁₀p₁₁+p₃p₇p₁₀p₁₂+p₃p₅p₈p₁₀+

+p₃p₈p₁₀+p₃p₈p₁₀p₁₁+p₃p₅p₉p₁₀+p₃p₉p₁₀p₁₁+p₃p₅p₇p₁₀+p₃p₅p₉p₁₀+

+p₁p₇p₈p₁₀+p₃p₇p₁₀p₁₂+p₃p₈p₉p₁₀+p₃p₉p₁₀p₁₂+p₃p₄p₅p₁₀+

+p₃p₄p₉p₁₀+p₃p₄p₇p₁₀+p₃p₄p₁₀p₁₂+p₃p₅p₈p₁₀+p₃p₉p₁₀p₁₁+

+p₃p₄p₉p₁₀+p₃p₅p₉p₁₀+p₃p₅p₇p₁₁+p₃p₇p₈p₁₁+p₁p₃p₅p₁₁+p₁p₃p₇p₁₁+

+p₁p₃p₁₁+p₁p₃p₅p₁₁+p₁p₃p₈p₁₁+p₁p₃p₁₁p₁₂+p₃p₄p₅p₁₁+p₃p₄p₉p₁₁+

+p₃p₄p₈p₁₁+p₃p₅p₇p₁₁+p₃p₇p₈p₁₁+p₃p₇p₉p₁₁+p₃p₇p₁₀p₁₁+p₃p₇p₉p₁₁++p₃p₇p₁₁p₁₂+p₃p₅p₈p₁₁+p₃p₈p₁₀p₁₁+p₃p₈p₁₁+p₃p₅p₉p₁₁+p₃p₉p₁₁+

+p₃p₅p₇p₁₁+p₃p₅p₈p₁₁+p₃p₅p₉p₁₁+p₃p₇p₈p₁₁+p₃p₇p₁₁p₁₂+p₃p₈p₉p₁₁++p₃p₈p₁₁p₁₂+p₃p₈p₁₁+p₃p₈p₁₁p₁₂+p₁p₃p₄p₁₁+p₃p₄p₉p₁₁+p₃p₄p₁₁+

+p₃p₄p₇p₁₁+p₃p₄p₁₁p₁₂+p₁p₃p₄p₁₁+p₁p₃p₈p₁₁+p₃p₅p₈p₁₁+p₃p₉p₁₁+

+p₃p₄p₉p₁₁+p₃p₅p₉p₁₁+p₅p₇p₈+p₅p₇p₈+p₁p₃p₅p₈+p₁p₅p₇p₈+

+p₁p₅p₈p₁₁+p₁p₅p₈p₁₁+p₃p₄p₅p₈+p₃p₅p₇p₈+p₃p₅p₈+p₃p₅p₈p₁₀+

+p₃p₅p₈p₁₁+p₃p₅p₈p₉+p₅p₇p₈p₉+p₅p₇p₈p₁₀+p₅p₇p₈p₁₁+p₅p₇p₈p₁₂+

+p₅p₈p₉+p₅p₈p₁₁+p₅p₈p₉p₁₀+p₅p₈p₉p₁₁+p₅p₈p₉p₁₂+p₅p₇p₈p₉+

+p₅p₇p₈p₁₀+p₅p₇p₈p₁₁+p₅p₇p₈p₁₂+p₅p₈p₉p₁₀+p₅p₈p₉p₁₁+p₅p₈p₁₁p₁₂++p₅p₈p₁₁+p₄p₅p₇p₈+p₄p₅p₈+p₄p₅p₈p₁₀+p₄p₅p₈p₁₁+p₄p₅p₈p₁₂+

+p₄p₅p₇p₈+p₄p₅p₈p₉+p₄p₅p₈p₁₂+p₃p₅p₈+p₃p₅p₉+p₅p₇p₁₁+

+p₅p₇p₈p₁₁+p₃p₄p₅p₁₁+p₁p₅p₇p₁₁+p₁p₅p₁₁+p₁p₅p₈p₁₁+p₁p₅p₁₁p₁₂+

+p₃p₄p₅p₁₁+p₃p₅p₇p₁₁+p₃p₅p₈p₁₁+p₃p₅p₈p₁₁+p₃p₅p₉p₁₁+p₃p₇p₈p₁₁+

+p₅p₇p₉p₁₁+p₅p₇p₁₀p₁₁+p₅p₇p₁₁+p₅p₇p₁₁p₁₂+p₅p₈p₉p₁₁+p₅p₈p₁₁+

+p₅p₉p₁₀p₁₁+p₅p₉p₁₁p₁₂+p₅p₉p₁₁+p₅p₇p₁₁p₁₂+p₅p₈p₁₁p₁₂+p₅p₈p₁₁+

+p₅p₉p₁₁p₁₂+p₁p₄p₅p₁₁+p₄p₅p₇p₁₁+p₄p₅p₈p₁₁+p₄p₅p₁₀p₁₁+p₄p₅p₁₁+

+p₄p₅p₁₁p₁₂+p₄p₅p₉p₁₁+p₃p₄p₅p₁₁+p₄p₅p₇p₁₁+p₄p₅p₁₁p₁₂+

+p₁p₄p₅p₁₁+p₁p₅p₈p₁₁+p₃p₅p₈p₁₁+p₃p₅p₉p₁₁+p₅p₇p₈p₉+p₇p₈p₉+

+p₁p₇p₈p₉+p₁p₈p₉p₁₁+p₃p₄p₈p₉+p₃p₇p₈p₉+p₃p₅p₈p₉+p₃p₈p₉p₁₀+

+p₃p₈p₉p₁₁+p₃p₅p₈p₉+p₅p₇p₈p₉+p₅p₈p₉+p₅p₈p₁₁+p₅p₈p₉p₁₁+

+p₅p₈p₉p₁₁+p₅p₈p₉p₁₀+p₇p₈p₉+p₇p₈p₉p₁₁+p₇p₈p₉p₁₂+p₇p₈p₉p₁₀+

+p₈p₉p₁₀+p₈p₉p₁₁+p₈p₉p₁₁p₁₂+p₈p₉p₁₀p₁₂+p₈p₉p₁₁p₁₂+p₄p₅p₈p₉+

+p₄p₇p₈p₉+p₄p₈p₉+p₄p₈p₉p₁₂+p₄p₈p₉p₁₀+p₄p₈p₉p₁₁+p₁p₄p₈p₉+

+p₁p₈p₉p₁₁+p₃p₅p₈p₉+p₃p₈p₉p₁₁+p₃p₄p₈p₉+p₃p₅p₈p₉+p₅p₇p₈p₁₀+

+p₇p₈p₁₀+p₁p₇p₈p₁₀+p₁p₈p₁₀p₁₁+p₃p₄p₈p₁₀+p₃p₇p₈p₁₀+p₃p₅p₈p₁₀+

+p₃p₈p₁₀+p₃p₈p₁₀p₁₁+p₅p₇p₈p₁₀+p₅p₈p₉p₁₀+p₅p₈p₁₀p₁₁+p₅p₈p₉p₁₀+

+p₇p₈p₉p₁₀+p₇p₈p₁₀p₁₁+p₇p₈p₁₀p₁₂+p₇p₈p₁₀+p₇p₈p₁₀p₁₂+p₈p₉p₁₀+

+p₈p₉p₁₀p₁₁+p₈p₁₀p₁₁p₁₂+p₈p₁₀p₁₁+p₈p₉p₁₀p₁₂+p₄p₅p₈p₁₀+

+p₄p₅p₈p₁₁+p₄p₇p₈p₁₀+p₄p₈p₉p₁₀+p₄p₈p₁₀p₁₂+p₄p₈p₉p₁₀+p₄p₇p₈p₁₀++p₄p₈p₁₀p₁₂+p₁p₄p₈p₁₀+p₄p₈p₁₀p₁₁+p₃p₅p₈p₁₀+p₅p₇p₉p₁₁+

+p₇p₈p₉p₁₁+p₁p₅p₉p₁₁+p₁p₈p₉p₁₁+p₁p₉p₁₁p₁₂+p₃p₄p₉p₁₁+p₃p₇p₉p₁₁+
+p₃p₈p₉p₁₁+p₃p₉p₁₁+p₅p₇p₉p₁₁+p₅p₈p₉p₁₁+p₅p₉p₁₀p₁₁+p₅p₉p₁₁p₁₂+

+p₃p₉p₁₁+p₇p₈p₉p₁₁+p₇p₉p₁₁p₁₂+p₈p₉p₁₀p₁₁+p₈p₉p₁₁+p₈p₉p₁₁p₁₂+

+p₈p₉p₁₁+p₉p₁₀p₁₁p₁₂+p₉p₁₁p₁₂+p₁p₄p₉p₁₁+p₄p₅p₉p₁₁+p₄p₇p₉p₁₁+

+p₄p₈p₉p₁₁+p₄p₉p₁₀p₁₁+p₄p₉p₁₁+p₄p₉p₁₁p₁₂+p₃p₄p₉p₁₁+p₄p₉p₁₁p₁₂++p₁p₄p₉p₁₁+p₁p₈p₉p₁₁+p₃p₉p₁₁+p₃p₄p₉p₁₁+p₃p₅p₉p₁₁+p₅p₇p₁₀p₁₁+

+p₇p₈p₁₀p₁₁+p₁p₃p₁₀p₁₁+p₁p₅p₁₀p₁₁+p₁p₈p₁₀p₁₁+p₁p_1ё0p₁₁p₁₂+

+p₃p₇p₁₀p₁₁+p₃p₈p₁₀p₁₁+p₃p₉p₁₀p₁₁+p₅p₇p₁₀p₁₁+p₅p₈p₁₀p₁₁+

+p₅p₉p₁₀p₁₁+p₇p₈p₁₀p₁₁+p₇p₁₀p₁₁p₁₂+p₈p₉p₁₀p₁₁+p₈p₁₀p₁₁p₁₂+

+p₈p₁₀p₁₁+p₉p₁₀p₁₁p₁₂+p₁p₄p₉p₁₁+p₄p₅p₁₀p₁₁+p₄p₉p₁₀p₁₁+

+p₄p₇p₁₀p₁₁+p₄p₁₀p₁₁p₁₂+p₃p₄p₁₀p₁₁+p₄p₇p₁₀p₁₁+p₄p₁₀p₁₁p₁₂+

+p₁p₄p₁₀p₁₁+p₁p₈p₁₀p₁₁+p₃p₉p₁₀p₁₁

СПmin=p₁p₃p₅+p₁p₃p₇+p₁p₃p₁₁+p₁p₅p₇+p₁p₅p₁₁+p₃p₄p₅+

+p₃p₄p₈+p₃p₄p₉++p₃p₄p₁₁+p₃p₅p₇+p₃p₅p₈+p₃p₅p₉+p₃p₇p₈+p₃p₇p₉+

+p₃p₇p₁₀+p₃p₇p₁₁+p₃p₇p₁₂+p₃p₈p₁₀+p₃p₈p₁₁+p₃p₉p₁₁++p₄p₅p₈+

+p₄p₅p₁₁+p₄p₈p₉+p₄p₉p₁₁+p₅p₇p₈+p₅p₇p₁₁+p₅p₈p₉+p₅p₈p₁₁+

+p₅p₉p₁₁+p₇p₈p₉+p₇p₈p₁₀+p₈p₉p₁₀+p₈p₉p₁₁+p₈p₁₀p₁₁+p₉p₁₁p₁₂+

+p₁p₃p₅p₇+p₁p₃p₇p₈+p₁p₃p₅p₁₁p₁p₃p₅p₈+p₁p₃p₅p₉+p₁p₃p₄p₅+

+p₁p₃p₄p₇+p₁p₃p₄p₈+p₁p₃p₄p₉+p₁p₃p₄p₁₁+p₁p₃p₄p₁₂+p₁p₃p₇p₉+

+p₁p₃p₇p₁₀+p₁p₃p₇p₁₁+p₁p₃p₇p₁₂+p₁p₃p₈p₁₀+p₁p₃p₈p₁₁+

+p₁p₃p₅p₁₀+p₁p₃p₉p₁₁+p₁p₃p₁₀p₁₁+p₁p₃p₁₁p₁₂+p₁p₄p₅p₇+p₁p₄p₅p₈++p₁p₄p₅p₁₀+p₁p₄p₅p₁₁+p₁p₄p₅p₁₂+p₁p₄p₇p₉+p₁p₄p₈p₉+p₁p₄p₇p₁₀+

+p₁p₄p₉p₁₀+p₁p₄p₉p₁₁+p₁p₄p₉p₁₂+p₁p₄p₁₀p₁₁+p₁p₄p₁₀p₁₂+p₁p₅p₇p₈++p₁p₅p₇p₉+p₁p₅p₇p₁₀+p₁p₅p₇p₁₁+p₁p₅p₇p₁₂+p₁p₅p₈p₉+p₁p₅p₈p₁₁+

+p₁p₅p₉p₁₀+p₁p₅p₉p₁₁+p₁p₅p₉p₁₂+p₁p₅p₁₀p₁₁+p₁p₅p₁₁p₁₂+p₁p₇p₈p₉++p₁p₇p₈p₉+p₁p₇p₈p₁₀+p₁p₇p₉p₁₂+p₁p₈p₉p₁₀+p₁p₇p₁₀p₁₂+p₁p₈p₉p₁₁+

+p₁p₈p₁₀p₁₁+p₁p₉p₁₀p₁₂+p₁p₉p₁₁p₁₂+p₁p₁₀p₁₁p₁₂+p₃p₅p₇p₈+

+p₃p₅p₇p₉+p₃p₅p₇p₁₀+p₃p₅p₇p₁₁+p₃p₅p₇p₁₂+p₃p₅p₈p₉+p₃p₅p₈p₁₀+p₃p₅p₈p₁₁+p₃p₅p₉p₁₀+p₃p₅p₉p₁₁+p₃p₅p₉p₁₂+p₃p₄p₅p₇+p₃p₄p₅p₈+

+p₃p₄p₅p₉+p₃p₄p₅p₁₀+p₃p₄p₅p₁₁+p₃p₄p₅p₁₂+p₃p₄p₇p₈+p₃p₄p₇p₉+

+p₃p₄p₇p₁₀+p₃p₄p₇p₁₁+p₃p₄p₈p₉+p₃p₄p₈p₁₀+p₃p₄p₈p₁₁+p₃p₄p₈p₁₂+

+p₃p₄p₉p₁₀+p₃p₄p₉p₁₁+p₃p₄p₉p₁₂+p₃p₄p₁₀p₁₁+p₃p₄p₁₀p₁₂+

+p₃p₄p₁₁p₁₂+p₃p₇p₈p₉+p₃p₇p₈p₁₀+p₃p₇p₈p₁₁+p₃p₇p₈p₁₂+p₃p₇p₉p₁₀+