Определение работоспособности сложного объекта

Объект будем называть сложным, если в его составе можно выделить ряд подсистем, имеющих самостоятельное значение и оцениваемых собственными условиями работоспособности. Следовательно сложный объект будет работоспособным, если работоспособны все входящие в его состав подсистемы, и будет неработоспособным, если хотя бы одна из этих подсистем окажется неработоспособной.

Пусть сложный объект содержит n подсистем, работоспособность каждой из которых может быть оценена по степени приближения только одного показателя x к его предельно допустимому значению Y.

Все контролируемые параметры объекта будут характеризоваться вектором 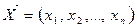. Тогда предельно допустимые значения этого вектора будут определяться вектором .

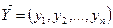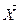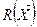Сопоставим вектору число таким образом, чтобы:

1) 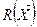было положительным и возрастало бы до ¥ при ;

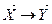2) если хотя бы один компонент x_i®y_i, то ;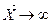

3) компонент, входящий в 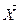с большим весом должен сильнее влиять на .

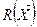Функцией, удовлетворяющей этим условиям может быть

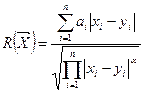(2.15)

где a_i > 0 – весовые коэффициенты.

Эта функция обладает тем свойством, что при x_i®y_i порядок числителя при стремлении к нулю ниже, чем порядок знаменателя при любом a>1 (так как в числителе сумма малых чисел, а в знаменателе корень квадратный из их произведения). Следовательно, 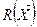будет стремиться к ¥ со скоростью 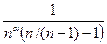. В частном случае, если a = 1, то эта скорость будет .

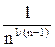Работоспособность сложного объекта может быть оценена выражением

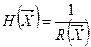(2.16)

В этом случае при приближении x_i к предельным значениям величина 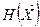будет изменяться от какого–то начального (максимального) значения до нуля.

Если каждая из подсистем тоже представляет собой сложный объект, то тогда для каждой из них можно подобрать (с помощью весовых коэффициентов a_i и показателя степени a) наиболее выгодные функции 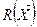, а следовательно, каждая подсистема будет характеризоваться своим совокупным показателем работоспособности 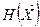, а общая работоспособность объекта может оцениваться их произведением.

В качестве весовых коэффициентов a_i в выражении (2.15) могут быть использованы значения корневых чувствительностей, рассмотренные в предыдущем параграфе.