Условия работоспособности объекта
Анализ работоспособности непрерывных объектов
Условия работоспособности объекта
Анализ работоспособности объекта предусматривает определение условий, при которых объект может выполнять возложенные на него функции. Эти условия называют условиями работоспособности объекта. Эти условия должны однозначно относить объект к одному из возможных состояний подмножества N1, характеризующего все возможные работоспособные состояния. Все состояния, не относящиеся к этому подмножеству будут неработоспособными. Для определения состояния объекта необходимо выбрать ряд параметров и характеристик объекта, по которым можно судить и его состоянии. А условия работоспособности накладывают ограничения на количественные значения или качественные показатели этих параметров и характеристик, что и позволяет осуществлять проверку работоспособности объекта.
Условия работоспособности можно сформулировать либо теоретически на основе анализа математической модели объекта, либо получить их экспериментально при исследовании реального объекта.
Для непрерывных линейных объектов условия работоспособности в общем случае могут быть заданы как ограничения на перемещения полюсов и нулей в комплексной плоскости, отображающей динамические свойства объекта (часто такую диаграмму называют фазовым портретом объекта). Задание области допустимых перемещений полюсов и нулей в комплексной плоскости позволяет формулировать условия работоспособности как ограничения на возможные значения корней передаточной функции. Отсюда можно перейти к заданию условий работоспособности во временной или частотной области по непосредственно измеряемым параметрам.
В качестве примера выполнения анализ работоспособности объекта, представляющего собой линейную систему второго порядка. Структурная схема объекта показана на рис. 2.1.
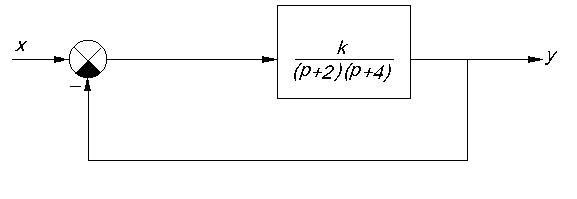
Рис. 2.1. Структурная схема линейного объекта второго порядка
Его передаточная функция имеет вид
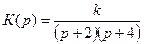
В качестве диагностической модели этого объекта может быть использовано характеристическое уравнение
(p+2)(p+4)+k = 0
p2+2p+4p+8+k = 0
p2+6p+(8+k) = 0
Корни этого уравнения (т.е. его полюсы) будут
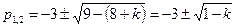
Таким образом, положение полюсов на комплексной плоскости определяется величиной k.
Если на комплексную плоскость нанести значения корней при различных величинах k, то мы получим фазовый портрет данного объекта.
Будем задавать значения k (коэффициент передачи системы) в области от 0 до +¥, т.к. он может быть только действительным числом.
Тогда, при k=0 p1,2 = –3±1, (p1 = –2, p2 = –4)
при k=1 p1 = p2 = –3
|
 при 0<k<1 корни выражаются действительными числами, лежащими между этими значениями (p1 – в области от –2 до –3, p2 – в области от –4 до –3). При всех значениях k>1 корни будут комплексными числами, вещественная часть которых равна –3, а мнимая часть равна
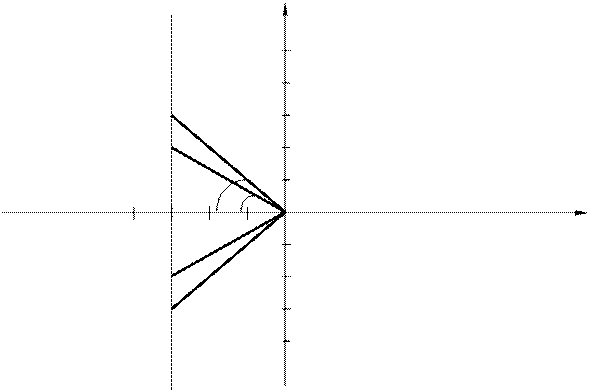
при 0<k<1 корни выражаются действительными числами, лежащими между этими значениями (p1 – в области от –2 до –3, p2 – в области от –4 до –3). При всех значениях k>1 корни будут комплексными числами, вещественная часть которых равна –3, а мнимая часть равна 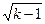 и у p1 – положительна, а у p2 – отрицательна. Таким образом, в этом случае корни располагаются на прямой параллельной мнимой оси и пересекающей действительную ось в точке –3 (см. рис. 2.2).
и у p1 – положительна, а у p2 – отрицательна. Таким образом, в этом случае корни располагаются на прямой параллельной мнимой оси и пересекающей действительную ось в точке –3 (см. рис. 2.2).
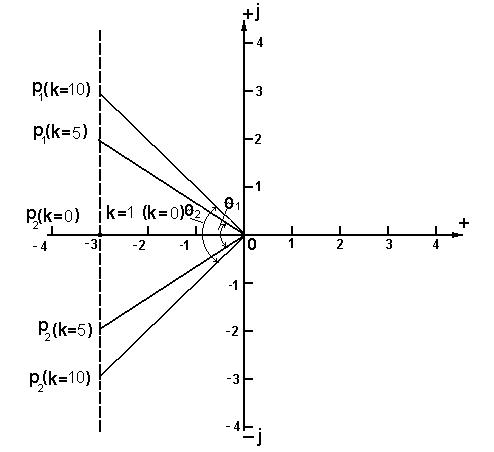 |
 Рис. 2.2. Положение корней характеристического уравнения на комплексной плоскости при изменении k от 0 до ¥.
Рис. 2.2. Положение корней характеристического уравнения на комплексной плоскости при изменении k от 0 до ¥.
Таким образом, корни характеристического уравнения могут быть либо вещественными и отрицательными, либо комплексно-сопряжёнными при отрицательной вещественной части.
Из теории автоматического регулирования известно, что при вещественных корнях система является апериодической с затухающим по экспоненте переходным процессом. Причём скорость затухания тем больше, чем больше абсолютное значение корней. При комплексно-сопряжённых корнях система будет колебательной, но поскольку вещественная часть корней отрицательна, то колебания будут затухающими. Причём скорость затухания будет определяться косинусом угла q прямой, соединяющей полюс p с началом координат. Поэтому величина cosq называется коэффициентом демпфирования системы.
Условия работоспособности системы могут соответствовать как апериодическому, так и колебательному режиму в зависимости от назначения и условий эксплуатации объекта. В соответствии с указанным выше общим методом указания условий работоспособности они могут быть заданы в виде допустимых областей перемещения полюсов. В нашем случае, если считать, что изменяться может только значение k, то полюса могут смещаться (при 0£k£1) только по вещественной оси от –2 до –4, а при k>1, только по вертикальной линии, проходящей через точку –3. Значит в первом случае ограничения накладываются на действительные значения корней (при этом мнимые части отсутствуют), а во втором случае – на мнимые части корней. В тех же случаях, когда могут изменяться и постоянные величины (заданные в характеристическом уравнении числами 6 и 8), то вместо вертикальной линии мы получаем вертикальный коридор определённой ширины.
Таким образом, можно последовательно перейти от условий работоспособности, заданных в виде ограничений, накладываемых на определённые качественные показатели работы объекта (статическая точность, динамическая точность, склонность к возникновению колебаний при скачкообразном изменении сигнала на входе, запас устойчивости системы и др.) к ограничениям, накладываемым на допустимые области полюсов (корней характеристического уравнения системы) на комплексной плоскости, а уже от них – к ограничениям на контролируемые параметры системы. Пусть в данном примере условия работоспособности заданы в виде допустимых значений коэффициента демпфирования системы, который определяет скорость затухания колебательных процессов при скачкообразном входном воздействии, т.е. в виде x1£x£x2, где x – коэффициент демпфирования системы. Тогда, учитывая, что x=cosq значениям x1 и x2, определяющим границы работоспособности, будут соответствовать значения углов q1 и q2 (см. рис. 2.2).
По ним мы определяем допустимые области полюсов системы на комплексной плоскости. Считая, что изменяться может только статический коэффициент передачи системы k, мы получаем область его допустимых значений. В данном случае она лежит между k=5 и k=10.
В общем случае для перехода от условий работоспособности, заданных в виде ограничений на допустимые перемещения корней характеристического уравнения в комплексной плоскости, к условиям работоспособности в виде ограничений, накладываемых на непосредственно контролируемые параметры объекта, используется метод малого параметра.
В частном случае, если контролируемый параметр l один, то диагностическая модель L(l)x записывается в виде характеристического уравнения, в которое в качестве одного из параметров входит l:
Ln(l)x=F(x,l), (2.1)
а его решение записывается в форме
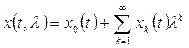 (2.2)
(2.2)
где: Ln – дифференциальный оператор порядка n, примененный к функции x(t), коэффициенты которого ai(t,l) являются непрерывными функциями t и аналитическими функциями контролируемого параметра l;
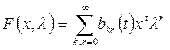 – аналитическая (в некоторой ограниченной области) функция двух параметров l и x.
– аналитическая (в некоторой ограниченной области) функция двух параметров l и x.
Применение метода малого параметра возможно при следующих условиях:
1) каждый коэффициент в разложении (2.2) определяется в результате конечного числа действий (т.е. число k – конечно);
2) ряд (2.2) сходится при достаточно малых l, где l – представляет собой приращение контролируемого параметра.
Проиллюстрируем применение метода малого параметра на нашем примере. Пусть k0=10. Тогда характеристическое уравнение будет иметь вид
p2 + 6p +18 = 0, (2.3)
а его корни равны
p1,2 = –3±3j (2.4)
Требуется определить допустимые изменения параметра k=k0+l, если условие работоспособности выражается в виде
[pj(0) – pj(l)] < di = 2, где j = 1, 2 (2.5)
Возмущённое характеристическое уравнение будет
p2 + 6p + [8+(k0+l)] = 0 (2.6)
Корни возмущённого уравнения представим рядом согласно (2.2), учитывая, что j=1,2 имеем лишь 2 члена ряда:
pj(l) = pj0 + pj1l +. (2.7)
Подставим их в выражение (2.6), заменив k0 его численным значением:
(pj0 + pj1l +...)2 + 6(pj0 + pj1l +...) +18 +l = 0
pj02 + 2 pj0pj1l + pj12l2 + 6pj0 + 6pj1+ pj1l +18 +l = 0 (2.8)
Учитывая (2.3), данное равенство должно выполняться при любых значениях p, откуда
p2j0 + 6pj0 + 18 = 0,
а значит сумма оставшихся членов (2.8) тоже должна быть равна нулю:
2pj0pj1l + pj12l2 + 6pj1l + l= 0,
пренебрегая членов второго порядка малости pj12l2 и сокращая l получим
2pj0 pj1+6pj1 + 1= 0(2.9)
Подставляя pj0 = –3±3j, получим
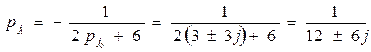
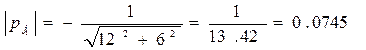
Условия работоспособности
|pj(0) – pj(l)| <2
Подставляя сюда значения pj(l) из (2.7) имеем
|pj(0) – (pj0 + pj1l)| <2,
откуда 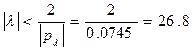 .
.
Таким образом, условия работоспособности будут выполняться при всех значениях k от 10 до 10+26.8 = 36.8.
В тех случаях, когда контролируемых параметров несколько, решение задачи является более сложным, но возможным, а условие работоспособности задаётся в виде:
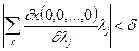 , (2.10)
, (2.10)
где x(0,0,...0) – исходная функция f(x) при подстановке в неё значений корней.
Дата добавления: 2017-03-29; просмотров: 1425;
