Тема 3 (1). Стандартные методы решения задачи моделирования предпочтений

(обзорно, в режиме повтора) Отношения предпочтения. Элементарные действия и свойства. Система предпочтений ЛПР. Выявление предпочтений: попарное сравнение, сортировка, ранжирование, балльное оценивание, относительная интенсивность, субъективные вероятности. Отношение как универсальная модель предпочтения. Нечеткие отношения предпочтений. Правило Родена о цепочках уточнений а) расширения текущей информации о предпочтениях и б) сужения текущего представления ядра отношения.

Если информация о предпочтениях ЛПР выявляется постепенно, т.е. сначала предпочтения описываются, например, отношением Raстрогого предпочтения, затем оно уточняется за счет дополнительной информации и расширяется до отношения Rb 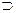Ra, то получится, что вначале (при отсутствии информации о предпочтениях ЛПР) можно будет выбирать только непосредственно из множества Dпредъявления (так как нет информации для различия элементов по предпочтению). Затем выбор следует делать из множества 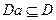, которое будет ядром отношения Rа, а затем уже из множества 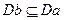, так как для построения функции выбора будет использовано более полное и совершенное отношение Rb.

В результате можно наблюдать две своеобразные цепочки отношений вложенности множеств:

ž цепочка уточнений (расширения) текущей информации о предпочтениях: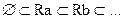

ž цепочка уточнений (сужения) текущего представления ядра отношения: .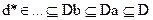

В соответствии с этими цепочками действует правило Родена: по мере расширения информации о предпочтениях (начиная с отсутствия информации, с пустого множества) и уточнения представлений ЛПР о том, чего оно желало бы видеть в качестве наилучшего своего выбора, постепенно сужается множество выбора (ядро отношения предпочтения), начиная со всего исходного множества Dпредъявления, и все явственнее просматривается наилучший элемент d*. Правило Родена (правила вложенных отношений) дает конструктивную основу для построения экономичных формальных процедур рационального выбора.

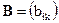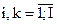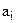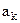Для количественного оценивания инертных критериев применяется 9-балльная шкала отношений. Матрица ( ) формируется в соответствии со степенями предпочтений критерия перед : элементам 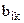приписывается 1 при одинаковой важности критериев, 3 – при умеренном предпочтении 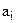перед 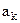, 5 – при существенном превосходстве, 7 – при значительном превосходстве, 9 – в случае абсолютного доминирования 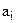перед 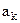, степени значимости 2,4,6,8 – интерпретируются как промежуточные суждения. При этом естественно выполнение 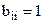; требование локальной согласованности достигается «автоматическим» условием 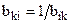(необходимо 0,5×I×(I-1) сравнений). Полную согласованность можно обеспечить «автоматическим» вычислением предпочтения 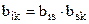(необходимо (I-1) сравнений). Но в таком случае оценка теряет «чистоту», а мы упускаем возможность проверить нашу точку зрения на искренность, уверенность. Матрица предпочтений отражает человеческие суждения, поэтому полную безошибочность при наличии довольно обширного спектра оттенков предпочтений трудно ожидать. Но если степень противоречий недопустима – индекс согласованности оценок 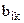превышает допустимый уровень 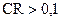, – предлагается пересмотреть оценки, т.к. нарушена логичность экспертного мнения.

Нормированный вектор приоритетов (весов) и коэффициент согласованности определяем методом собственного значения (применяется один из приближенных методов, т.к. при большой размерности матричные операции все равно сводятся к численным итерационным процедурам). Вариант расчета: нормируем матрицу 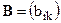так, что 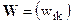, где 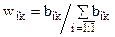(элементы каждого столбца исходной матрицы относим к сумме элементов этого же столбца). Элементы вектора весов 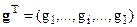есть средневзвешенные элементов соответствующих строк нормированной матрицы, т.е. 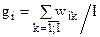, 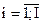и фактически представляют собственный вектор, отвечающий максимальному собственному значению l_max матрицы сравнения 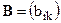. Приближенное значение l_max определяем из уравнения 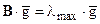, где 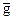есть среднее арифметическое компонент вектора , или в явном виде:

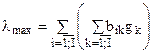
Индекс согласованности CR матрицы B рассчитываем как отношение коэффициента согласованности CI этой матрицы к стохастическому коэффициенту согласованности RI:

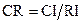, где ,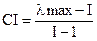

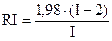
Если значение индекса не превышает значение 0.1, рассогласование матрицы Bсчитается допустимым.

Заметим, что для большой группы экспертов допустимо предположение о нормальном распределении результатов оценивания. Модификация обработки и анализа попарных суждений проводится в различных направлениях, например, метод Терстоуна использует не средние, а медианные расчеты (см. литературу по принятию управленческих решений).

Альтернативой единственному агрегированному (обобщенному) показателю является математический аппарат типа многокритериальной оптимизации - множества Парето и т.д.