Ранжирование>Альтернатива Кондорсе
Снова рассмотрим наш пример (табл. 36.7).
| Таблица 36.7. Распределение мест проектов, данное коллективом экспертов
|
| | A
| B
| C
| D
| | Эксперт 1
|
|
|
|
| | Эксперт 2
|
|
|
|
| | Эксперт 3
|
|
|
|
| | Эксперт 4
|
|
|
|
| |
Сначала для каждой пары проектов (i и j) подсчитаем, какое количество Sij экспертов считает, что i-ый проект лучше, чем j-ый, и какое количество Sji экспертов считает наоборот (см. табл. 36.8).
| Таблица 36.8. Расчет отношений «лучше-хуже» между проектами
|
| Sij
| Отношение
| Sji
| Пояснение
| | SAB = 3
| >
| SBA = 1
| A лучше B
| | SAC = 4
| >
| SCA = 0
| A лучше C
| | SAD = 4
| >
| SDA = 0
| A лучше D
| | SBC = 3
| >
| SCB = 1
| B лучше C
| | SBD = 3
| >
| SDB = 1
| B лучше D
| | SCD = 3
| >
| SDC = 1
| C лучше D
| |
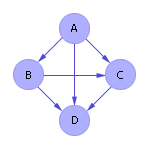
Далее на графе стрелками покажем отношения между парами проектов (см. рис. 36.3). Стрелка от i-го проекта в графе к j-му указывает, что i-му проекту отдали предпочтение больше экспертов, чем j-му. Например, стрелка от A направлена к B, так как проект A лучше проекта B (трое экспертов предпочли проекту B проект A, и лишь только один эксперт — наоборот).
| |
| Рис. 36.3. Граф предпочтений проектов АВСD
|
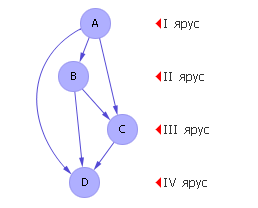
Теперь упорядочим граф, приведя его к ярусно-параллельной форме (ЯПФ) (см. рис. 36.4).
| |
| Рис. 36.4. Граф предпочтений ABCD в ярусно-параллельной форме
|
Приведение графа к ЯПФ есть приведение его к такой форме, где в верхних ярусах находятся вершины, в которые нет входящих стрелок из вершин, лежащих в нижних ярусах. Алгоритм построения ЯПФ графа разбирается в дисциплине «Дискретная математика». Итак, ЯПФ показывает, что вершиной, в которую нет стрелок, является вершина A, следовательно, абсолютным лидером среди проектов является проект A. Проект A лучше B, одновременно он лучше C, одновременно он лучше D. Далее, среди оставшихся проектов (BCD) проект B лучший, так как он одновременно лучше C и D. И, наконец, C лучше D.
Ответ: проект A — 1 место, проект B — 2 место, проект C — 3 место, проект D — 4 место. Наилучшим проектом является проект A.
Дата добавления: 2019-10-16; просмотров: 867;