Точность и доверие к результатам экспертизы. Оценка экспертов
Важным вопросом экспертизы является формирование группы экспертов. Если экспертов много, то в группу с высокой вероятностью попадают некомпетентные эксперты. Если экспертов мало, то результат экспертизы существенно зависит от конкретных лиц, попавших в число экспертов. Поэтому имеет смысл, опросив экспертов ri и получив результат экспертизы R, оценить объективность каждого из членов экспертного коллектива по следующей формуле:
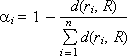
|
Для нашего примера можно просчитать объективность каждого эксперта. Рассмотрим уже полученное ранее решение (см. табл. 36.15).
| Таблица 36.15. Матрица мнений экспертов и результат экспертизы | ||||||||||||||||||||||||||||||
|
Расстояние d(ri, R) от мнения i-го эксперта до результата (среднего мнения R):
d(r1, R) = |1 – 1| + |2 – 2| + |3 – 3| + |4 – 4| = 0;
d(r2, R) = |1 – 1| + |3 – 2| + |2 – 3| + |4 – 4| = 2;
d(r3, R) = |2 – 1| + |1 – 2| + |3 – 3| + |4 – 4| = 2;
d(r4, R) = |1 – 1| + |3 – 2| + |4 – 3| + |2 – 4| = 4.
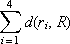 = 0 + 2 + 2 + 4 = 8.
= 0 + 2 + 2 + 4 = 8.
α1 = 1 – 0/8 = 1;
α2 = 1 – 2/8 = 0.75;
α3 = 1 – 2/8 = 0.75;
α4 = 1 – 4/8 = 0.5.
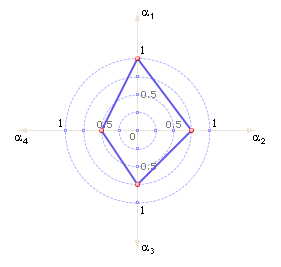
Итак, как видим, первый эксперт имеет наибольшую объективность; наименьшую объективность имеет четвертый эксперт (см. рис. 36.8). Кстати, неслучайно в методе «Медиана Кемени» мнение первого эксперта было принято в качестве ответа экспертизы, а четвертый эксперт стоял на периферии многоугольника мнений экспертов ABCD (см. рис. 36.1 и рис. 36.2)…
| |
| Рис. 36.8. Диаграмма объективности экспертов |
Вообще-то рекомендуется отсеять мнения экспертов с малым значением α и результат R пересчитать снова без их учета.
Вторая проверка экспертов касается согласованности их коллектива. Для расчета согласованности мнений рассчитаем дисперсию мнений (см. табл. 36.16) и оценим ее величину статистической формулой W = 12 · D/(n2 · (m3 – m)), где n — число экспертов, m — число проектов.
| Таблица 36.16. Матрица расчета согласованности мнений экспертов для группы из четырех экспертов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Для нашего случая имеем: W = 12 · 46/(42 · (43 – 4)) = 552/960 = 0.575. При W = 1 эксперты находятся в полном согласии; при W = 0 наблюдается полная несогласованность. В нашем примере согласие экспертов слабое. Поэтому можно порекомендовать изменить число экспертов — либо удалить четвертого эксперта, как самого необъективного, либо увеличить число экспертов для большей статистической устойчивости результатов. Посмотрим, как возрастет согласованность экспертов, например, после удаления четвертого эксперта (см. табл. 36.17).
| Таблица 36.17. Матрица расчета согласованности мнений экспертов для группы из трех экспертов | |||||||||||||||||||||||||||||||||||||||||||||||||
|
W = 12 · 29/(32 · (43 – 4)) = 0.64 — как видим, согласие увеличилось.
Таким образом, экспертиза помогает нам провести неформальный анализ в моделировании, отобрав из множества предложенных методами генерации идей наиболее перспективный вариант будущего проекта. В выбранный проект в дальнейшем будут вложены значительные средства для его детализации (процесс проектирования и моделирования — см. Понятие моделирования. Способы представления моделей и Рис. 1.14. Схема процесса, способов и приемов моделирования (полный вариант)).
Обычно для уверенного принятия решения, так как все методы экспертиз субъективны, используют сразу несколько методов и выводят общее решение.
Полученное решение обязательно следует проверить. Мы рассмотрели две проверки — на качество эксперта (объективность эксперта) и качество группы (согласованность группы).
Сама величина критерия, полученная в результате проверки, дает только относительную оценку. Рекомендуется наблюдать изменение величины в результате изменения некоторого существенного фактора и добиваться наилучшего значения этой величины, сознательно управляя этим фактором (см., например, табл. 36.16 и табл. 36.17). Таким фактором чаще всего может служить величина группы, качественный состав группы экспертов, система критериев, состав проектов. Хорошие результаты дает применение итераций в экспертизе.
Но всегда следует иметь в виду, что никакое количество проверок, даже очень большое, не гарантирует абсолютной правильности выбора решения.
Ранжирование (процесс упорядочения), как правило, применяется к качественным (атрибутивным) признакам объекта наблюдения (факторам), для которых не удается (невозможно) установить точную числовую шкалу измерения интенсивности признака: объекты можно установить лишь в порядке убывания качества. Мерой качества субъективных оценок является их рассеяние ® ранговая корреляция Кендалла или Спирмена: определение тесноты связи между а) ранжировками произвольного числа признаков двух экспертов или б) двух признаков на основании мнения произвольного числа экспертов. Коэффициент конкордации Кендалла: оценка согласованности мнений экспертов в группе, содержащей более 2-х экспертов.
Метод Саати – метод анализа иерархий:
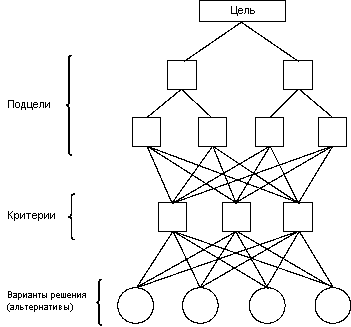
Рисунок - Декомпозиция целей
Для каждой «связки» определенного уровня дерева иерархии одним из способов строим свои вектора приоритетов удовлетворительной степени согласованности (или заданной точности) 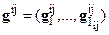 , здесь
, здесь 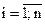 - номер уровня иерархии,
- номер уровня иерархии, 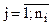 – номер связки
– номер связки 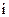 -го уровня,
-го уровня, 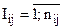 -количество критериев j-ой связки i-го уровня (очевидно, количество связок равно числу критериев предыдущего уровня). Относительно фокуса (главного уровня иерархии) вектор приоритетов рассчитывается по известному принципу выделения ветвей-звеньев дерева по логическим признакам: логическое «и» подразумевает умножение весов, логическое «или» – сложение. Таким образом, интегрированный относительно каждого уровня показатель есть сумма произведений значений соответствующих факторов на «вес» этого фактора. В случае необходимости вектор
-количество критериев j-ой связки i-го уровня (очевидно, количество связок равно числу критериев предыдущего уровня). Относительно фокуса (главного уровня иерархии) вектор приоритетов рассчитывается по известному принципу выделения ветвей-звеньев дерева по логическим признакам: логическое «и» подразумевает умножение весов, логическое «или» – сложение. Таким образом, интегрированный относительно каждого уровня показатель есть сумма произведений значений соответствующих факторов на «вес» этого фактора. В случае необходимости вектор 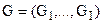 нормируется величиной
нормируется величиной 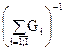 .
.
Вектор G позволяет принять решение в условиях многокритериальности, т.к. его компоненты выражают агрегированные предпочтения ЛПР в отношении альтернатив. Если 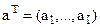 отражает причинные факторы, описывающие главную цель иерархии U, то функция полезности имеет вид
отражает причинные факторы, описывающие главную цель иерархии U, то функция полезности имеет вид 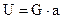 (произведение вектора-строки на вектор-столбец):
(произведение вектора-строки на вектор-столбец):
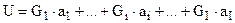
Значение весового коэффициента Gi интерпретируется как величина среднего изменения результата U с изменением фактора ai на единицу (в случае долевых единиц измерения факторов ai имеем процентное изменение U).
Для статистической значимости коэффициентов функции полезности типа уравнения регрессии, необходима представительная выборка достаточного объема. Метод анализа иерархий дает возможность построения функциональной зависимости по гораздо меньшему числу наблюдений включенных в нее факторов.
Функцию 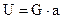 , в зависимости от содержательной нагрузки ai (и вида измерения), можно использовать в традиционных целях:
, в зависимости от содержательной нагрузки ai (и вида измерения), можно использовать в традиционных целях:
Ÿ получения точечных и интервальных оценок краткосрочного прогноза U; в этом случае проводится аналитическое выравнивание временных рядов по всем факторам ai, входящим в модель, и по полученным зависимостям ai(t) строится точечный прогноз 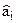 (здесь уместно применение методов сглаживающих или адаптивных), а также стандартная ошибка и доверительный интервал;
(здесь уместно применение методов сглаживающих или адаптивных), а также стандартная ошибка и доверительный интервал;
Ÿ оптимизации «распределения» ресурсов ai: построение задачи линейного (дробно-линейного) программирования оптимизации U с ограничениями на ai (возможно двусторонними);
Ÿ для оценки эффективности управления системой: сопоставлением потенциальной (p) и плановой (q) величин целевого результата U:
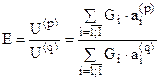
Функцию 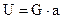 , как индикатор стратегической эффективности, можно использовать двояко:
, как индикатор стратегической эффективности, можно использовать двояко:
1. инструментальная функция предназначена для обоснования стратегических решений;
2. оценочная функция пригодна для подведения итогов и стимулирования.
Дата добавления: 2019-10-16; просмотров: 794;

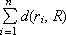 — сумма расстояний от всех мнений экспертов до среднего мнения R.
— сумма расстояний от всех мнений экспертов до среднего мнения R.