Тема 3(3). Прикладные задачи выбора решений в условиях целевой неопределенности

Одношаговые методы решения многокритериальной задачи: обобщенный критерий, «затраты-эффект», целевое программирование, главный критерий. Многошаговые методы решения задачи выбора по векторному критерию: метод последовательных уступок, оптимизация по функции ценности. Метод жесткого ранжирования.

На практике более адекватным отображением реальной ситуации является векторное (матричное или более сложное образование) представление стратегии оперирующей стороны. Пусть стратегия представляет собой вектор 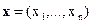, где компоненты 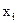связаны рядом ограничений с конкретным экономическим и физическим существом задачи:

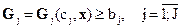
где 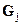- векторная функция, 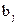- фиксированная скалярная величина, 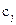- совокупность фиксированных величин (скаляр, вектор и т.п.). Ограничения определяют область допустимых стратегий 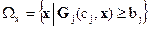. ЛПР управляет операцией (ИП), выбирая из области 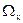ту или иную стратегию x.

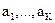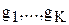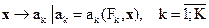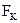Эффективность действий оценивается совокупностью частных (локальных) критериев , которые отличаются важностью (коэффициентами относительной важности) и характеризуют некоторую локальную цель всей операции. Каждый частный критерий связан со стратегией некоторым отображением , где - совокупность фиксированных факторов. Частный случай отображения 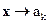- функциональная зависимость (на практике часто довольствуются экспертными оценками).

Одновременное достижение цели операции (принятия инвестиционного многокритериального решения) по всем частным критериям за счет выбора единой стратегии x невозможно, то необходимо достижение некоторого компромисса в решении проблемы поиска оптимальной стратеги:

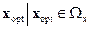- , т.е. стратегия должна быть достижима;

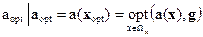- , т.е. стратегия должна быть наилучшей в смысле принятого в задаче принципа компромисса с учетом вектора важности 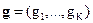локальных критериев 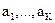. Конкретный смысл оператора оптимальности opt указывается в каждой конкретной задаче принятия инвестиционного решения.

Для ускорения описанной процедуры можно проводить фильтрацию допустимых решений. Суть фильтрации состоит в разбиении области допустимых решений на два непересекающихся подмножества:

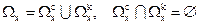
где 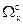- область согласия (качество решения можно улучшить одновременно по всем направлениям либо не снизить уровень любого из критериев);

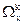- область компромисса (улучшение качества решения по одному или нескольким направлениям ухудшает качество решения по другим направлениям).

Очевидно, оптимальное решение принадлежит области компромисса, т.к. в области согласия решение может (а, значит, должно) быть улучшено по всем критериям. Для выбора одного варианта решения из отфильтрованного подмножества решений необходимо раскрыть смысл оператора оптимальности (выбрать схему компромисса), что носит субъективный характер ЛПР.

Заметим, что проведение схемы компромисса предполагает нормализацию частных критериев (сведение либо к величинам одинаковой размерности, либо к безразмерным относительным величинам) и одинаковую важность каждого критерия. Анализ схемы компромисса можно сузить аналогичной фильтрацией: область 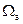выбираемых решений представить в виде двух подмножеств области согласия и компромисса относительно смысла оператора opt: 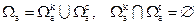. Тогда модель выбора оптимальной стратегии можно представить так:

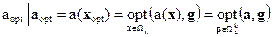
Отметим, что основными схемами компромисса являются принцип равномерности, принцип справедливой уступки, принцип последовательной уступки.