Поиск наилучшей паретовской точки
Постановка задачи
Пусть решение 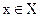 , где
, где 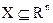 - множество допустимых решений в пространстве параметров, описано значениями критериев
- множество допустимых решений в пространстве параметров, описано значениями критериев 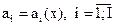 , формирующими образ
, формирующими образ 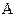 множества
множества 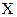 в критериальном пространстве:
в критериальном пространстве:
для 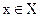
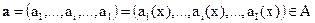
Каждый из I критериев преобразован так, что его надо максимизировать для улучшения качества решения 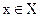 . Пусть существует не заданная в явном виде функция качества, отражающая предпочтения ЛПР об эффективности решения x на основе информации о значениях критериев
. Пусть существует не заданная в явном виде функция качества, отражающая предпочтения ЛПР об эффективности решения x на основе информации о значениях критериев 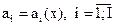 :
:
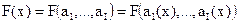
Предположим, что ЛПР для любых 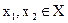 по значениям
по значениям 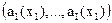 и
и 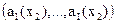 может:
может:
- указать лучшее решение, чему соответствует 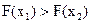 либо
либо 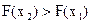 ;
;
- установить эквивалентность решений, чему соответствует 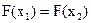 .
.
Формализация задачи поиска лучшего решения такова:
найти 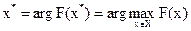
|
дея решения: сократим исходное множество решений до множества Парето и сведем поиск лучшего решения к поиску на выделенном множестве.
Решение x или a в пространстве параметров оптимально по Парето, если его невозможно улучшить ни по одному из критериев без ухудшения хотя бы по одному из критериев. Парето-оптимальные решения образуют множество Парето 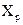 в пространстве параметров или
в пространстве параметров или 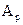 в пространстве критериев.
в пространстве критериев.
Обозначим вектор коэффициентов значимости
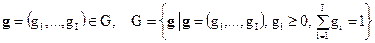
Тогда множество Парето описывается следующими моделями:
для выпуклых множеств
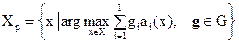
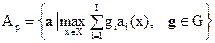
|
для невыпуклых множеств
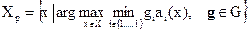
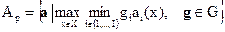
|
Если известно оптимальное по Парето решение 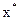 :
:
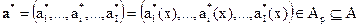 ,
,
то оно может быть записано через модели ( 2) и ( 3):
для выпуклых множеств
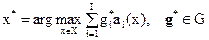
|
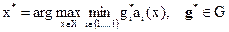
|
Существует соответствие между наилучшей паретовской точкой 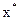 и точкой
и точкой 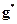 во множестве всех весов G (т.е. имеется возможность устанавливать соответствие между однокритериальной и многокритериальной задачами).
во множестве всех весов G (т.е. имеется возможность устанавливать соответствие между однокритериальной и многокритериальной задачами).
Из анализа моделей ( 2) и ( 3) очевидно, что меняя веса, получаем различные паретовские точки. Эта связь позволяет свести поиск наилучшего решения из пространства критериев A в пространство весов G, что, в свою очередь, позволяет уменьшить размерность задачи за счет нормированности весовых векторов: 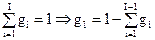
Итак, задача состоит в поиске наилучшей, с точки зрения ЛПР, точки 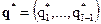 такой, что
такой, что
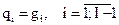 ,
, 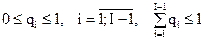
Алгоритм решения
В алгоритме используется метод покоординатного спуска. Правило останова: процесс поиска предполагается либо до получения оптимального решения, либо до выполнения определенного числа шагов.
1. Задать начальные параметры:
длина шага 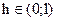 ;
;
постоянный коэффициент изменения длины шага 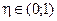 ;
;
начальная точка (решение) 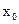 ;
;
начальный весовой вектор 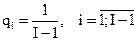
2. Установить 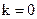 .
.
3. Вычислить 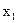 , решив задачу максимизации
, решив задачу максимизации
для выпуклого множества Парето в критериальном пространстве: 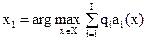
для невыпуклого множества: 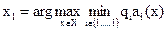
4. Проверить правило останова. Если условие выполняется, поиск прекратить, причем решением будет:
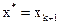 ;
; 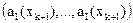 ;
; 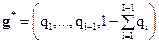
5. 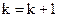
6. Установить
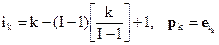
где 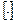 - целая часть числа
- целая часть числа 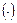 ,
,
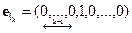 -
- 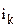 -е координатное направление
-е координатное направление
7. Уменьшить 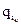 на величину шага h, сохранив другие компоненты вектора q неизменными
на величину шага h, сохранив другие компоненты вектора q неизменными
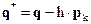
8. Проверить выполнение ограничений
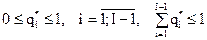
|
Если значение 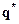 недопустимо, перейти к п.11; в противном случае установить
недопустимо, перейти к п.11; в противном случае установить 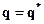 .
.
9. Определить 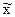 , решив задачу максимизации с установленным q:
, решив задачу максимизации с установленным q:
для выпуклого множества
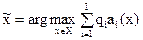
|
для невыпуклого множества
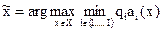
10. ЛПР сравнивает точки (решения) 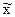 и
и 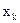 . Если
. Если 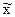 лучше, чем
лучше, чем 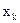 , то принять
, то принять 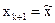 и перейти к п.4.
и перейти к п.4.
11. Увеличить 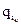 на величину шага h, сохранив другие компоненты вектора q неизменными
на величину шага h, сохранив другие компоненты вектора q неизменными 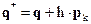
12. Проверить выполнение ограничений ( 6). Если значение 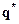 недопустимо, перейти к п.15; в противном случае установить
недопустимо, перейти к п.15; в противном случае установить 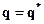 .
.
13. Определить
|
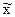 , решив задачу максимизации ( 7) с установленным q.
, решив задачу максимизации ( 7) с установленным q.
14. ЛПР сравнивает точки (решения) 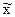 и
и 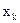 . Если
. Если 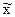 лучше, чем
лучше, чем 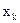 , то принять
, то принять 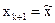 и перейти к п.4.
и перейти к п.4.
15. 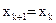
16. Если 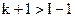 и вектор q не изменился за последние (I-1) итераций, изменить длину шага:
и вектор q не изменился за последние (I-1) итераций, изменить длину шага: 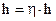
17. Перейти к п.4
Результат работы алгоритма выбора наилучшей паретовской точки кроме решения 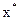 (оптимального с точки зрения ЛПР) возвращает соответствующий весовой вектор
(оптимального с точки зрения ЛПР) возвращает соответствующий весовой вектор 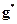 , который представляет собой информацию о предпочтениях конкретного ЛПР (информацию можно использовать для дальнейшего исследования).
, который представляет собой информацию о предпочтениях конкретного ЛПР (информацию можно использовать для дальнейшего исследования).
Отметим свойства рассмотренного метода:
- Метод выбора наилучшей паретовской точки можно использовать как метод выявления предпочтения ЛПР (нахождения весового вектора в промежуточных расчетах).
- Наличие весового вектора позволяет ускорить процесс имитационного моделирования поведения ЛПР.
Дата добавления: 2019-10-16; просмотров: 596;
