Алгебраический момент силы относительно точки
Основные понятия статики
В статике твердого тела рассматриваются свойства сил, приложенных к твердому телу. В частности, изучается приведение сложных систем сил к более простому виду и устанавливаются условия равновесия различных систем сил, действующих на твердое тело или материальную точку.
Материальная точка – простейшая модель материального тела любой формы, размеры которого достаточно малы и которое можно принять за геометрическую точку, имеющую определенную массу.
Механической системой называется любая совокупность материальных точек, положение и движение которых между собой связаны.
Абсолютно твердым телом (или неизменяемой механической системой) называют механическую систему, расстояния между точками которой не изменяются при любых взаимодействиях.
Силой называют одну из векторных мер действия одного материального объекта на другой рассматриваемый объект. Сила кроме числового значения характеризуется точкой приложения и направлением действия. Она является векторной величиной. Силу как величину векторную обозначают какой-либо буквой со знаком вектора, например 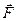 или
или 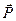 . Для выражения числового значения силы или ее модуля используется знак модуля от вектора, т.е.
. Для выражения числового значения силы или ее модуля используется знак модуля от вектора, т.е. 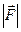 ,
, 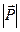 или те же буквы, но без знака вектора, т. е.
или те же буквы, но без знака вектора, т. е. 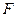 ,
, 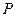 .
.
Системой сил 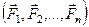 называют совокупность сил, действующих на рассматриваемый материальный объект.
называют совокупность сил, действующих на рассматриваемый материальный объект.
Системой сил, эквивалентной нулю (или равновесной системой сил), называют такую систему сил, действие которой на твердое тело или материальную точку, находящиеся в покое или движущиеся по инерции, не приводит к изменению состояния покоя или движения по инерции этого тела или материальной точки.
Две системы сил 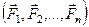 и
и 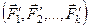 называются эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях. Условие эквивалентности двух систем сил
называются эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях. Условие эквивалентности двух систем сил 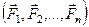 и
и 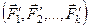 выражают в форме:
выражают в форме:
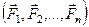 ~
~ 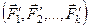 ,
,
где 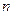 и
и 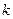 – число сил в системах.
– число сил в системах.
Равнодействующей силой рассматриваемой системы сил называют силу, действие которой на твердое тело или материальную точку эквивалентно действию этой системы сил. Равнодействующая сила обозначается 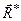 , условие ее эквивалентности рассматриваемой системе сил
, условие ее эквивалентности рассматриваемой системе сил 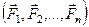 выражается в виде:
выражается в виде:
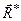 ~
~ 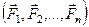 .
.
Отметим, что не каждая система сил имеет равнодействующую
Уравновешивающей силой заданной системы сил считается такая сила, добавление которой к заданной дает новую систему, эквивалентную нулю. Если 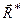 является уравновешивающей силой системы сил
является уравновешивающей силой системы сил 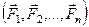 , то, согласно определению, она удовлетворяет условию:
, то, согласно определению, она удовлетворяет условию:
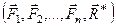 ~0.
~0.
Момент силы
Алгебраический момент силы относительно точки
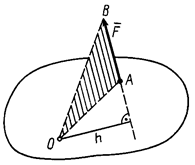
Алгебраическим моментом силы 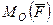 относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус (рис. 1).
относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус (рис. 1).
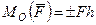 . (1)
. (1)
 Плечом
Плечом 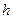 силы
силы 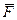 относительно точки называют кратчайшее расстояние между этой точкой и линией действия силы, т.е. длину отрезка перпендикуляра, опущенного из точки
относительно точки называют кратчайшее расстояние между этой точкой и линией действия силы, т.е. длину отрезка перпендикуляра, опущенного из точки 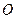 на линию действия силы
на линию действия силы 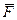 .
.
Если сила стремится вращать тело вокруг моментной точки (точки, относительно которой вычисляют алгебраический момент силы) против часовой стрелки, то берем знак плюс, если по часовой стрелке – знак минус.
 Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю.
Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю.
Дата добавления: 2017-09-19; просмотров: 982;
