Корреляционный момент, коэффициент корреляции
Особую роль играет центральный смешанный момент второго порядка 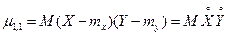 , называемый корреляционным моментом или моментом связи.
, называемый корреляционным моментом или моментом связи.
Корреляционным моментом (или ковариацией) двух случайных величин X и Y называется математическое ожидание произведения отклонений этих случайных величин от их математических ожиданий и обозначается через 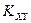 или
или 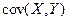 .
.
Таким образом, по определению
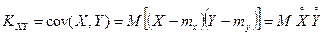 . .
| (6.28) |
При этом: если  - дискретная двумерная случайная величина, то ковариация вычисляется по формуле
- дискретная двумерная случайная величина, то ковариация вычисляется по формуле
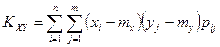 , ,
| (6.29) |
если  - непрерывная двумерная случайная величина, то
- непрерывная двумерная случайная величина, то
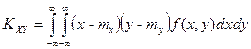 . .
| (6.30) |
Ковариацию часто удобно вычислять по формуле
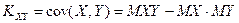 . .
| (6.31) |
Формулу (6.30) можно записать в виде
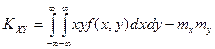 . .
| (6.32) |
Свойства ковариации:
1. Ковариация симметрична, т.е.
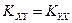 .
.
2. Дисперсия случайной величины, есть ковариация ее с самой собой, т.е.
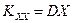 ,
, 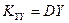 .
.
3. Если случайные величины X и Y независимы, то
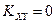
4. Дисперсия суммы (разности) двух случайных величин равна сумме их дисперсий плюс (минус) удвоенная ковариация этих случайных величин, т. е.
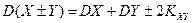 .
.
5. Постоянный множитель можно вынести за знак ковариаций, т.е.
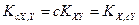 или
или 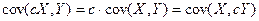 .
.
6. Ковариация не изменится, если к одной из случайных величин (или к обоим сразу) прибавить постоянную, т.е.
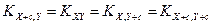
или
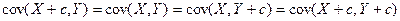 .
.
7. Ковариация двух случайных величин по абсолютной величине не превосходит их среднего квадратического отклонения, т.е.
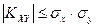 .
.
Из свойства 3 следует, что если 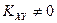 , то случайные величины Х и Y зависимы. Случайные величины Х и Y в этом случае (
, то случайные величины Х и Y зависимы. Случайные величины Х и Y в этом случае ( 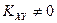 ) называют коррелированными. Однако из того, что
) называют коррелированными. Однако из того, что 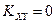 , не следует независимость случайных величин Х и Y. В этом случае случайные величины Х и Y называют некоррелированными. Из независимости вытекает некоррелированность; обратное не верно.
, не следует независимость случайных величин Х и Y. В этом случае случайные величины Х и Y называют некоррелированными. Из независимости вытекает некоррелированность; обратное не верно.
Из свойств ковариации следует, что она ( 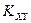 ) характеризует и степень зависимости случайных величин, и их рассеяние вокруг точки
) характеризует и степень зависимости случайных величин, и их рассеяние вокруг точки 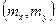 . Размерность ковариации равна произведению размерностей случайных величин Х и Y. В качестве числовой характеристики зависимости (а не рассеяния) случайных величин Х и Y берут безразмерную величину – коэффициент корреляции. Он является лучшей оценкой степени влияния одной случайной величины на другую.
. Размерность ковариации равна произведению размерностей случайных величин Х и Y. В качестве числовой характеристики зависимости (а не рассеяния) случайных величин Х и Y берут безразмерную величину – коэффициент корреляции. Он является лучшей оценкой степени влияния одной случайной величины на другую.
Коэффициентом корреляции 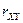 двух случайных величин Х и Y называют отношение их ковариации (корреляционного момента) к произведению их средних квадратических отклонений:
двух случайных величин Х и Y называют отношение их ковариации (корреляционного момента) к произведению их средних квадратических отклонений:
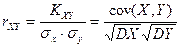 . .
| (6.33) |
Очевидно, коэффициент корреляции равен ковариации стандартных случайных величин 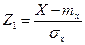 и
и 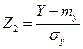 , т.е.
, т.е. 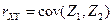
Свойствакоэффициента корреляции:
1. Коэффициент корреляции по абсолютной величине не превосходит 1, т.е.
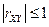 или
или 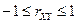 .
.
2. Если Х и Y независимы, то
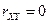 .
.
3. Если Х и Y связаны линейной зависимостью 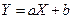 ,
, 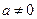 , то
, то
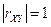 ,
,
причем 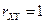 при
при 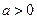 ,
, 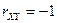 при
при 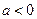 .
.
4. Если 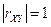 , то случайные величины Х и Y связаны линейной функциональной зависимостью.
, то случайные величины Х и Y связаны линейной функциональной зависимостью.
Итак, для независимых случайных величин 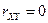 , для линейно связанных
, для линейно связанных 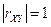 , а в остальных случаях
, а в остальных случаях 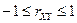 .
.
Говорят, что случайные величины связаны положительной корреляцией, если 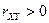 , а если
, а если 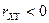 - отрицательной корреляцией. Чем ближе
- отрицательной корреляцией. Чем ближе 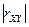 к единице, тем больше оснований считать, что X и Y связаны линейной зависимостью. Отметим, что корреляционные моменты и дисперсии системы случайных величин обычно задаются корреляционной матрицей:
к единице, тем больше оснований считать, что X и Y связаны линейной зависимостью. Отметим, что корреляционные моменты и дисперсии системы случайных величин обычно задаются корреляционной матрицей:
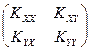 или или 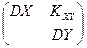 . .
| (6.34) |
Пример 6.6.Закон распределения дискретной двумерной случайной величины задан таблицей:
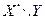
| -1 | ||
| 0,15 | 0,40 | 0,05 | |
| 0,20 | 0,10 | 0,10 |
Найти коэффициент корреляции 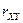 .
.
Решение:
Находим законы распределения составляющих X и Y:
| Х | Y | -1 | |||||||
| Р | 0,6 | 0,4 | р | 0,35 | 0,50 | 0,15 |
Найдем математические ожидания составляющих:
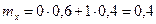 ,
,
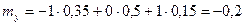
(их можно было найти и по формуле (6.20)).
Находим дисперсии составляющих:
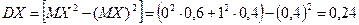 ,
,
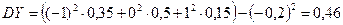 .
.
Тогда 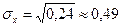 ,
, 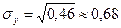 .
.
Находим MХY, используя формулу (6.26):
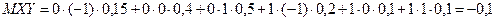
(Можно было составить закон распределения Z=XY, а затем найти MZ=MXY:
| Z=XY | -1 | ||
| p | 0,20 | 0,70 | 0,10 |
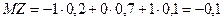 ).
).
Находим корреляционный момент, используя формулу (6.31):
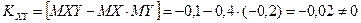 .
.
Находим коэффициент корреляции по формуле (6.33):
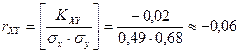 - отрицательная корреляция.
- отрицательная корреляция.
Двумерное нормальное распределение
Среди законов распределения двумерной случайной величины  на практике чаще всего встречается нормальное (гауссовское) распределение вероятностей. Оно применяется, в частности, для описания 2-х результатов измерения, абсциссы и ординаты точки попадания
на практике чаще всего встречается нормальное (гауссовское) распределение вероятностей. Оно применяется, в частности, для описания 2-х результатов измерения, абсциссы и ординаты точки попадания  при стрельбе и т.д.
при стрельбе и т.д.
Двумерная случайная величина  называется распределенной по нормальному закону, если ее совместная плотность
называется распределенной по нормальному закону, если ее совместная плотность 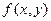 имеет вид
имеет вид
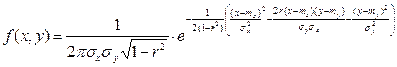 , ,
| (6.35) |
где mх, mу, σх, σу, 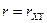 - параметры этого распределения.
- параметры этого распределения.
Распределение (6.35) называется также нормальным законом распределения на плоскости или двумерным нормальным (гауссовским) распределением.
Можно доказать, что 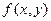 - это функция плотности, т.е. справедливо равенство
- это функция плотности, т.е. справедливо равенство
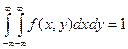 ,
,
mx = MX, my = MY; σx и σy - средние квадратические отклонения; r - коэффициент корреляции случайных величин X и Y.
Это означает, что двумерное нормальное распределение полностью определяется заданием его числовых характеристик, что удобно на практике (опытным путем находят эти параметры-характеристики и получают совместную плотность 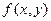 двух нормально распределенных случайных величин X и У).
двух нормально распределенных случайных величин X и У).
Выясним смысл параметров 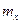 и
и 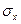 , найдя распределение вероятностей составляющих Х (т.е. плотность вероятностей одномерной случайной величины Х).
, найдя распределение вероятностей составляющих Х (т.е. плотность вероятностей одномерной случайной величины Х).
Согласно (6.10) имеем:
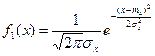 . .
| (6.36) |
Случайная величина Х имеет нормальное распределение с математическим ожиданием 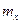 и дисперсией
и дисперсией 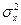 . Аналогично получаем
. Аналогично получаем
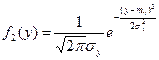 , ,
| (6.37) |
т.е. 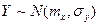 .
.
График плотности 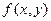 нормально распределенной двумерной случайной величины
нормально распределенной двумерной случайной величины  представляет собой холмообразную поверхность, вершина которой находится в точке
представляет собой холмообразную поверхность, вершина которой находится в точке 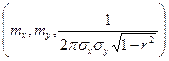 , т.е. максимум функции
, т.е. максимум функции 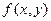 достигается в точке
достигается в точке 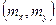 (рис. 5.13, гл.V).
(рис. 5.13, гл.V).
Если компоненты двумерной нормально распределенной случайной величины  некоррелированы
некоррелированы 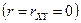 , то функция плотности (6.35) принимает вид
, то функция плотности (6.35) принимает вид
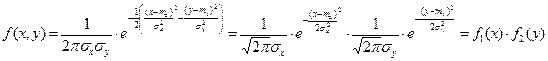 , ,
| (6.38) |
т.е.
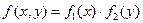 ,
,
где 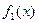 - плотность распределения случайной величины Х,
- плотность распределения случайной величины Х, 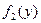 - случайной величины Y.
- случайной величины Y.
Следовательно, некоррелированные нормально распределенные случайные величины являются также и независимыми, и наоборот. Таким образом, для нормально распределенных случайных величин термины «независимость» и «некоррелированность» эквивалентны.
Утверждение. Если случайные величины Х и Y независимы, то вероятность попадания случайной точки  , распределенной по нормальному закону в прямоугольник
, распределенной по нормальному закону в прямоугольник 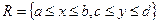 , находится по формуле:
, находится по формуле:
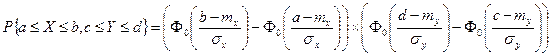 ,
,
где 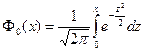 - функция Лапласа.
- функция Лапласа.
Произвольную область D можно приближенно заменить областью, составленной из прямоугольников. На этом основано применение так называемых «сеток рассеивания».
Пример 6.7. Найти вероятность попадания точки  в прямоугольник
в прямоугольник 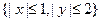 , если плотность совместного распределения случайных величин Х и Y равна
, если плотность совместного распределения случайных величин Х и Y равна 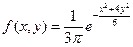 .
.
Решение:
Функцию 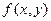 можно переписать в виде
можно переписать в виде
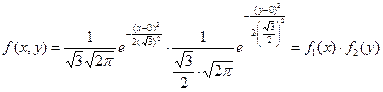
Значит Х и Y независимы и 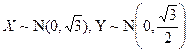 .
.
Поэтому 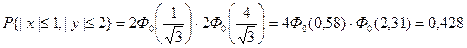 .
.
Дата добавления: 2017-03-29; просмотров: 1356;
