Многомерные случайные величины
Многомерная (n-мерная) случайная величина (общие сведения)
Систему n случайных величин называют n-мерной (многомерной) случайной величиной или случайным вектором 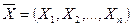 .
.
Многомерная случайная величина есть функция элементарного события w: 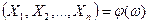 : каждому элементарному событию w ставится в соответствие n действительных чисел
: каждому элементарному событию w ставится в соответствие n действительных чисел 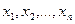 - значения, принятые случайными величинами
- значения, принятые случайными величинами 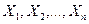 в результате опыта. Вектор
в результате опыта. Вектор 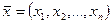 называется реализацией случайного вектора
называется реализацией случайного вектора 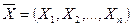 .
.
Закон распределения вероятностей n-мерной случайной величины задается ее функцией распределения
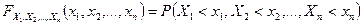
Функция распределения 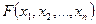 обладает такими же свойствами, как и функция распределения двух случайных величин
обладает такими же свойствами, как и функция распределения двух случайных величин 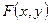 . В частности: она принимает значения на отрезке [0, 1],
. В частности: она принимает значения на отрезке [0, 1],
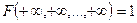 ,
,
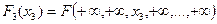 .
.
Плотность распределения системы n непрерывных случайных величин 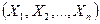 определяется равенством
определяется равенством
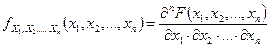 .
.
При 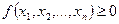 и
и
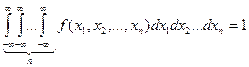
Вероятность попадания случайной точки 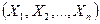 в область D из n-мерного пространства выражается n-кратным интегралом
в область D из n-мерного пространства выражается n-кратным интегралом
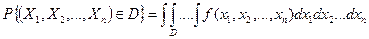 .
.
Функция распределения 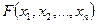 выражается через плотность
выражается через плотность 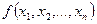 n-кратным интегралом
n-кратным интегралом
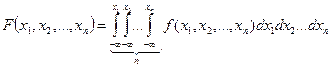
Необходимым и достаточным условием взаимной независимости n случайных величин является равенство:
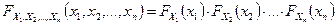 ,
,
а для n непрерывных случайных величин
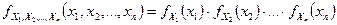 .
.
Основными числовыми характеристиками многомерной случайной величины 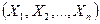 являются:
являются:
1. n математических ожиданий составляющих 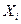 , т.е.
, т.е.
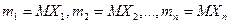
2. n дисперсий составляющих 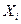 , т.е.
, т.е.
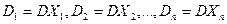 ,
,
при этом 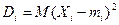 ,
, 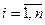 .
.
3. n(n - 1) ковариаций, т.е.
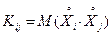 ,
, 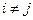 ,
,
при этом 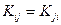 ,
, 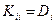 .
.
Ковариации 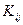 образуют ковариационную матрицу
образуют ковариационную матрицу
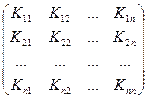 или
или 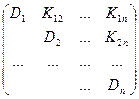
Дата добавления: 2017-03-29; просмотров: 257;
