Зависимость и независимость двух случайных величин

Зная законы распределения случайных величин X и Y, входящих в систему , можно найти закон распределения системы только в случае, когда случайные величины X и Y - независимы.

Две случайные величины называются независимыми, если закон распределения каждой из них не зависит от того, какие значения принимает другая. В противном случае случайные величины называются зависимыми.

Теперь дадим общее определение независимости случайных величин.

Случайные величины X и Y называются независимыми, если независимыми являются события 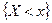и 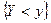для любых действительных х и у. В противном случае случайные величины называются зависимыми.

Сформулируем условие независимости случайных величин.

Теорема 6.1.Для того, чтобы случайные величины X и Y были независимы, необходимо и достаточно, чтобы функция распределения системы была равна произведению функций распределения составляющих:

.

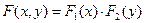(6.11)

Доказательство. Если случайные величины X и Y независимы, то события 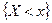и 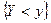независимы. Следовательно, 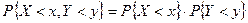, т.е. .

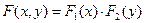Если же имеет место равенство (6.11), то 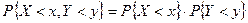. Значит, случайные величины X и Y независимы.

Заметим, что условие (6.11) - это иначе записанное условие независимости двух событий: 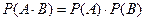для случая событи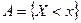й и .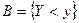

Теорема 6.2.Необходимым и достаточным условием независимости двух непрерывных случайных величин, образующих систему , является равенство

.

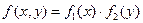(6.12)

Доказательство. Если X и Y независимые непрерывные случайные величины, то имеет место равенство (6.11). Дифференцируя это равенство по х, а затем по у, получим 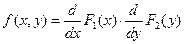или .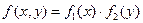

И обратно. Интегрируя равенство (6.12) по х и по у, получим

,

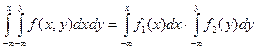т.е. 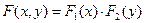. На основании теоремы 6.1 заключаем, что случайные величины X и У независимы.

Теорема 6.3.Необходимым и достаточным условием независимости двух дискретных случайных величин X и Y, образующих систему , является равенство

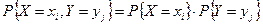
(6.13)

для любых , .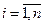

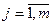Пример. 6.4. Зависимы или независимы случайные величины Х и Y, рассмотренные в примерах 6.1 и 6.3?

Решение:

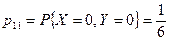а) , а 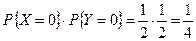, т.е. 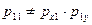. Случайные величины Х и Y зависимы.

б) 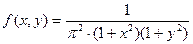, а 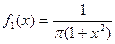, 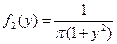. Так как 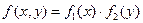, то согласно условию (6.12) случайные величины Х и Y независимы.