Плотность распределения вероятностей двумерной случайной величины и ее свойства
Исчерпывающей характеристикой непрерывной двумерной случайной величины является плотность вероятности. Вводится это понятие аналогично тому, как это делалось при рассмотрении плотности распределения вероятностей одной случайной величины.
Двумерная случайная величина называется непрерывной, если ее функция распределения 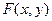 есть непрерывная функция, дифференцируемая по каждому из аргументов, у которой существует вторая смешанная производная
есть непрерывная функция, дифференцируемая по каждому из аргументов, у которой существует вторая смешанная производная  .
.
Плотностью распределения вероятностей (или совместной плотностью) непрерывной двумерной случайной величины  называется вторая смешанная производная ее функции распределения.
называется вторая смешанная производная ее функции распределения.
Обозначается совместная плотность системы двух непрерывных случайных величин  через
через 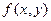 (или
(или  ). Таким образом, по определению
). Таким образом, по определению
 . .
| (6.6) |
Плотность распределения вероятностей непрерывной двумерной случайной величины  есть предел отношения вероятности попадания случайной точки
есть предел отношения вероятности попадания случайной точки  в элементарный прямоугольник со сторонами
в элементарный прямоугольник со сторонами 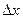 и
и  , примыкающий к точке
, примыкающий к точке 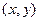 , к площади этого прямоугольника, когда его размеры
, к площади этого прямоугольника, когда его размеры 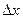 и
и  стремятся к нулю (рис. 6.4).
стремятся к нулю (рис. 6.4).
По аналогии с плотностью вероятности одномерной непрерывной случайной величины, для двумерной случайной величины  плотность вероятности определяется как функция
плотность вероятности определяется как функция 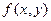 , удовлетворяющая условию
, удовлетворяющая условию
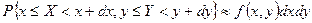 . .
| (6.7) |
выражение 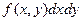 называется элементом вероятности двумерной случайной величины
называется элементом вероятности двумерной случайной величины  .
.
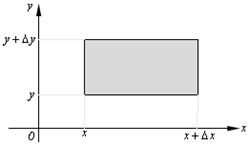
Рис. 6.4.
Геометрически плотность распределения вероятностей 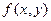 системы двух случайных величин
системы двух случайных величин  представляет собой некоторую поверхность, называемую поверхностью распределения (рис. 6.5).
представляет собой некоторую поверхность, называемую поверхностью распределения (рис. 6.5).

Рис. 6.5.
Плотность распределения 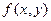 обладает следующимисвойствами:
обладает следующимисвойствами:
1. Плотность распределения двумерной случайной величины неотрицательна, т.е.

2. Вероятность попадания случайной точки  в область D равна двойному интегралу от плотности по области D, т.е.
в область D равна двойному интегралу от плотности по области D, т.е.
 . .
| (6.8) |
3. Функция распределения двумерной случайной величины может быть выражена через ее плотность распределения по формуле:
 . .
| (6.9) |
4. Условие нормировки: двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице, т. е.
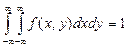 .
.
Геометрически свойство 4 означает, что объем тела, ограниченного поверхностью распределения и плоскостью Оху, равен единице.
5. Плотность распределения одномерных составляющих Х и У могут быть найдены по формулам:
 , ,  . .
| (6.10) |
Пример 6.3. Двумерная случайная величина  задана плотностью распределения вероятностей
задана плотностью распределения вероятностей 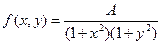 .
.
Найти: 1) А; 2) 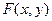 ; 3)
; 3)  ; 4)
; 4) 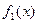 и
и 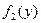 .
.
Решение:
1) Постоянную А найдем, используя условие нормировки:
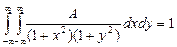 ,
,
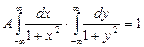 ,
,
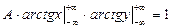 ,
, 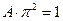
Следовательно,  .
.
2) Используя формулу (6.9), находим:
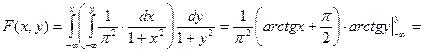
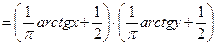 .
.
3) По формуле (6.2) находим 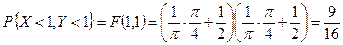 .
.
4) по формуле (6.10) получаем:
 ,
,
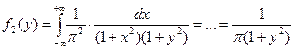
Дата добавления: 2017-03-29; просмотров: 307;
