Понятие о системе случайных величин и законе ее распределения
Двумерные случайные величины
При изучении случайных явлений часто приходится иметь дело с двумя, тремя и большим числом случайных величин. Совместное рассмотрение нескольких случайных величин приводит к системам случайных величин. Так, точка попадания снаряда характеризуется системой  двух случайных величин: абсциссой X и ординатой Y; успеваемость наудачу взятого абитуриента характеризуется системой n случайных величин
двух случайных величин: абсциссой X и ординатой Y; успеваемость наудачу взятого абитуриента характеризуется системой n случайных величин 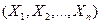 - оценками, проставленными в его аттестате зрелости.
- оценками, проставленными в его аттестате зрелости.
Упорядоченный набор 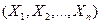 случайных величин
случайных величин 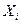
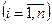 , заданных на одном и том же ПЭС Ω, называется n-мерной случайной величиной или системой n случайных величин.
, заданных на одном и том же ПЭС Ω, называется n-мерной случайной величиной или системой n случайных величин.
Одномерные случайные величины 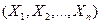 называются компонентами или составляющими n-мерной случайной величины
называются компонентами или составляющими n-мерной случайной величины 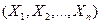 . Их удобно рассматривать как координаты случайной точки или случайного вектора
. Их удобно рассматривать как координаты случайной точки или случайного вектора 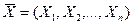 в пространстве n измерений.
в пространстве n измерений.
На многомерные случайные величины распространяются почти без изменений основные понятия и определения, относящиеся к одномерным случайным величинам. Ограничимся для простоты рассмотрением системы двух случайных величин; основные понятия обобщаются на случай большего числа компонент.
Упорядоченная пара  двух случайных величин Х и Y называется двумерной случайной величиной или системой двух одномерных случайных величин X и Y.
двух случайных величин Х и Y называется двумерной случайной величиной или системой двух одномерных случайных величин X и Y.
Систему  можно изобразить случайной точкой
можно изобразить случайной точкой 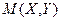 или случайным векторомОМ (рис.6.1).
или случайным векторомОМ (рис.6.1).
Система  есть функция элементарного события:
есть функция элементарного события: 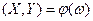 . Каждому элементарному событию
. Каждому элементарному событию 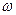 ставится в соответствие два действительных числа х и у (или х1 и x2) - значения X и Y (или
ставится в соответствие два действительных числа х и у (или х1 и x2) - значения X и Y (или 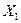 и
и 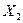 ) в данном опыте. В этом случае вектор
) в данном опыте. В этом случае вектор 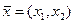 называется реализацией случайного вектора
называется реализацией случайного вектора 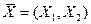 .
.
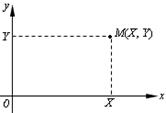
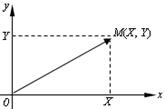
Рис. 6.1.
Системы случайных величин могут быть дискретными, непрерывнымии смешанными в зависимости от типа случайных величин, образующих систему. В первом случае компоненты этих случайных систем дискретны, во втором - непрерывны, в третьем - разных типов.
Полной характеристикой системы  является ее закон распределения вероятностей, указывающий область возможных значений системы случайных величин и вероятности этих значений. Как и для отдельных случайных величин закон распределения системы может иметь разные формы (таблица, функция распределения, плотность, ...).
является ее закон распределения вероятностей, указывающий область возможных значений системы случайных величин и вероятности этих значений. Как и для отдельных случайных величин закон распределения системы может иметь разные формы (таблица, функция распределения, плотность, ...).
Так, закон распределения дискретной двумерной случайной величины  можно задать формулой
можно задать формулой
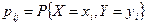 , , 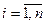 , , 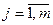
| (6.1) |
или в форме таблицы с двойным входом:
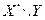
| 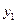
| 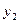
| 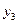
| … | 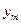
|
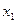
| 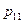
| 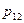
| 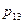
| … | 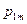
|
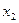
| 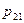
| 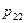
| 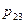
| … | 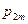
|
| … | … | … | … | … | … |
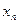
| 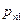
| 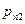
| 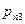
| … | 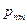
|
Причем, сумма всех вероятностей 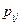 , как сумма вероятностей полной группы несовместных событий
, как сумма вероятностей полной группы несовместных событий 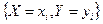 , равна единице:
, равна единице:
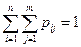 .
.
Зная закон распределения дискретной случайной величины, можно найти законы распределения каждой из компонент (обратное неверно). Так, 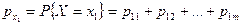 , что следует из теоремы сложения несовместных событий
, что следует из теоремы сложения несовместных событий 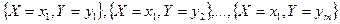 .
.
Аналогично можно найти
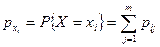 ,
,
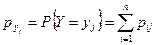 .
.
Пример 6.1. В урне 4 шара: 2 белых, 1 черный, 1 синий. Из нее наудачу извлекают два шара. Пусть случайная величина Х – число черных шаров в выборке, случайная величина Y – число синих шаров в выборке. Составить закон распределения для системы  . Найти законы распределения X и Y.
. Найти законы распределения X и Y.
Решение:
Случайная величина Х может принимать значения 0, 1; случайная величина Y - значения 0, 1.
Вычислим вероятности
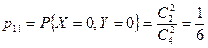 или
или 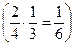 ,
,
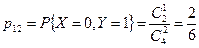 ,
,
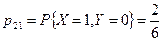 ,
,
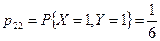 .
.
Таблица распределения системы  имеет вид:
имеет вид:
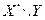
| ||
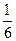
| 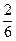
| |
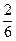
| 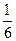
|
Отсюда следует:
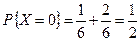 ,
,
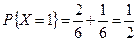 ,
,
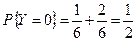 ,
,
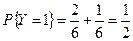 .
.
Законы распределения составляющих X и Y имеют вид:
| Х | Y | |||||||
| р | 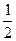
| 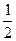
| р | 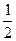
| 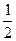
|
Дата добавления: 2017-03-29; просмотров: 370;
