Условные законы распределения
Если случайные величины Х и Y, образующие систему  , зависимы между собой, то для характеристики их зависимости вводится понятие условных законов распределения случайных величин.
, зависимы между собой, то для характеристики их зависимости вводится понятие условных законов распределения случайных величин.
Условным законом распределения одной из случайных величин, входящей в систему  , называется ее закон распределения, найденный при условии, что другая случайная величина приняла определенное значение (или попала в какой-то интервал).
, называется ее закон распределения, найденный при условии, что другая случайная величина приняла определенное значение (или попала в какой-то интервал).
Пусть  - дискретная двумерная случайная величина и
- дискретная двумерная случайная величина и 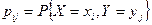 ,
, 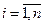 ,
, 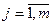 . Напомним, что условная вероятностей событий
. Напомним, что условная вероятностей событий 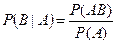 . Тогда условная вероятность того, что случайная величина Y примет значение
. Тогда условная вероятность того, что случайная величина Y примет значение  при условии, что
при условии, что 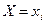 определяется равенством
определяется равенством
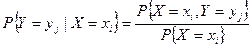 , , 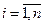 , , 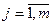 . .
| (6.14) |
Совокупность вероятностей (6.14), т.е. 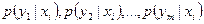 , представляет собой условный закон распределения случайной величины Y при условии
, представляет собой условный закон распределения случайной величины Y при условии 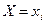 . Сумма условных вероятностей
. Сумма условных вероятностей 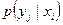 равна 1, действительно:
равна 1, действительно:
 . .
| (6.15) |
Аналогично определяются условная вероятность, условный закон распределения случайной величины Х при условии 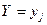 .
.
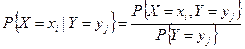 , , 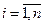 , , 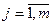 . .
| (6.16) |
Пусть теперь  - непрерывная двумерная случайная величина с плотностью
- непрерывная двумерная случайная величина с плотностью 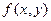 ,
, 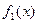 и
и 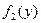 - плотности распределения соответственно случайной величины Х и случайной величины Y.
- плотности распределения соответственно случайной величины Х и случайной величины Y.
Плотность вероятности условного распределения(илиусловная плотность) случайной величины Y при условии Х = х определяется равенством:
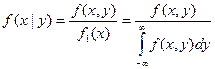 , где , где 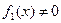 . .
| (6.17) |
Условная плотность обладает свойствами плотности распределения, так
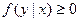 ,
, 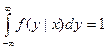
Аналогично определяется условная плотность распределения случайной величины Х при условии Y = у:
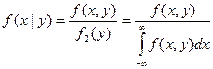 , где , где 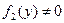 . .
| (6.18) |
Используя соотношения (6.17) и (6.18) можно записать
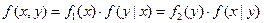 , ,
| (6.19) |
т.е. совместная плотность распределения системы случайных величин равна произведению плотности одной составляющей на условную плотность другой составляющей при заданном значении первой.
Равенство (6.19) называют теоремой (правилом) умножения плотностей распределения.
В случае произвольного типа случайных величин функция распределения 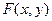 системы зависимых случайных величин
системы зависимых случайных величин  может быть записана в виде:
может быть записана в виде:
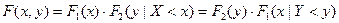 ,
,
где 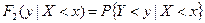 - условная функция распределения случайной величины Y при условии
- условная функция распределения случайной величины Y при условии 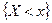 ;
; 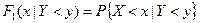 - условная функция распределения случайной величины Х при условии
- условная функция распределения случайной величины Х при условии 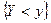 .
.
Пример 6.5. Задана таблица распределения двумерной случайной величины  :
:
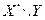
| |||
| 0,1 | 0,12 | 0,08 | 0,40 |
| 0,2 | 0,16 | 0,10 | 0,14 |
Найти: а) безусловные законы распределения случайных величин Х и Y; б) условный закон распределения случайной величины Х при Y=2.
Решение:
а) Так как 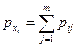 и
и 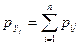 , то
, то
| Х | 0,1 | 0,2 | Y | ||||||
| р | 0,6 | 0,4 | р | 0,28 | 0,18 | 0,54 |
б) С учетом формулы (6.16) имеем:
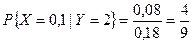 ,
,
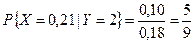 .
.
Таким образом, условный закон распределения случайной величины Х при Y=2 таков
| Х | 0,1 | 0,2 |
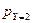
| 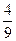
| 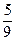
|
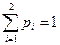 .
.
Очевидно, несовпадение условного и безусловного законов распределения случайной величины Х. Следовательно, случайные величины Х и Y зависимы.
Дата добавления: 2017-03-29; просмотров: 259;
