Регрессия. Теорема о нормальной корреляции
При изучении двумерной случайной величины рассматриваются не только числовые характеристики одномерных компонент X и Y, но и числовые характеристики условных распределений: условные математические ожидания, условные дисперсии.
Условным математическим ожиданием одной из случайных величин, входящих в систему 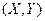 называется ее математическое ожидание, вычисляемое при условии, что другая случайная величина приняла определенное значение (или попала в данный интервал). Обозначается:
называется ее математическое ожидание, вычисляемое при условии, что другая случайная величина приняла определенное значение (или попала в данный интервал). Обозначается: 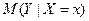 или
или 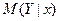 и
и 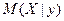 .
.
Вычисляются эти характеристики по обычным формулам математического ожидания, в которых вместо плотности распределения и вероятностей событий используются условные плотности распределения или условные вероятности.
Для непрерывных случайных величин
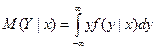 , , 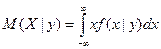 , ,
| (6.39) |
где 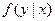 и
и 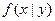 - условные плотности распределения случайных величин X и Y.
- условные плотности распределения случайных величин X и Y.
Для дискретных случайных величин X и Y условные математические ожидания вычисляются по формулам
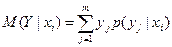 , , 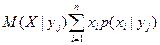 . .
| (6.40) |
где 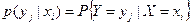 ,
, 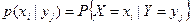 .
.
Условное математическое ожидание случайной величины Y при заданном X = х, т.е. 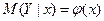 , называется функцией регрессии или просто регрессией Y на x (или Y по х). Аналогично,
, называется функцией регрессии или просто регрессией Y на x (или Y по х). Аналогично, 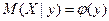 - регрессия X на у (или X по у).
- регрессия X на у (или X по у).
Графики этих функций называются соответственно линиями (или кривыми) регрессии Y на х и X на у.
Если обе функции регрессии Y на х и X на у линейны, то говорят, что случайные величины X и Y связанылинейной корреляционной зависимостью.
Теорема 6.4 (Теорема о нормальной корреляции).Если двумерная случайнвя величина 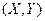 распределена по нормальному закону, то случайные величины X и Y связанылинейной корреляционной зависимостью. (Примем теорему без доказательства).
распределена по нормальному закону, то случайные величины X и Y связанылинейной корреляционной зависимостью. (Примем теорему без доказательства).
Условный закон распределения является нормальным с условным математическим ожиданием и условной дисперсией, определяемыми формулами:
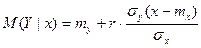 , , 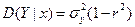 . .
| (6.41) |
Можно получить функцию регрессии Х на у:
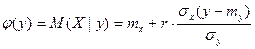 и и 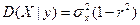 . .
| (6.42) |
Пример 6.8. Построить линию регрессии Y на х для двумерной случайной величины 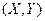 , закон распределения которой задан таблицей:
, закон распределения которой задан таблицей:
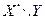
| -1 | 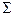
| ||
| 0,1 | 0,15 | 0,2 | 0,45 | |
| 0,15 | 0,25 | 0,15 | 0,55 | |
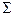
| 0,25 | 0,4 | 0,35 |
Решение:
Находим условные ряды распределения случайной величины Y при 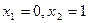 , используя формулы (6.14).
, используя формулы (6.14).
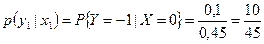 ,
,
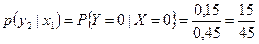 ,
,
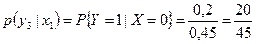 .
.
Согласно (6.40) имеем
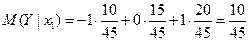 .
.
Далее:
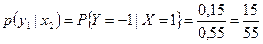 ,
,
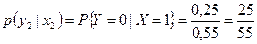 ,
,
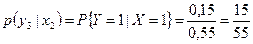 .
.
Следовательно,
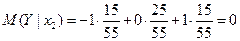 .
.
Линия регрессии Y на х изображена на рис. 6.6.
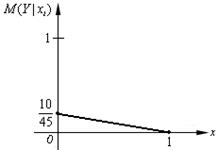
Рис.6.6.
Дата добавления: 2017-03-29; просмотров: 896;
