Математическое ожидание и дисперсия двумерной случайной величины

Для системы случайных величин также вводятся числовые характеристики, подобные тем, какие были для одной случайной величины. В качестве числовых характеристик системы обычно рассматривают моменты различных порядков. На практике чаще всего используются моменты I и II порядков, математическое ожидание, дисперсия и корреляционный момент. Математическое ожидание и дисперсия двумерной случайной величины служат соответственно средним значением и мерой рассеяния. Корреляционный момент выражает меру взаимного влияния случайных величин, входящих в систему .

Математическим ожиданием двумерной случайной величины называется совокупность двух математических ожиданий MX и MY, определяемых равенствами:

, ,

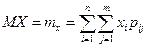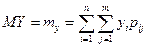(6.20)

если - дискретная система случайных величин (здесь 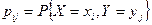); и

, ,

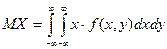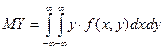(6.21)

если - непрерывная система случайных величин (здесь f(x, y) — плотность распределения системы).

Дисперсией системы случайной величины называется совокупность двух дисперсий DX и DY, определяемых равенствами:

, ,

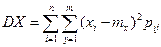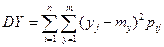(6.22)

если - дискретная система случайных величин.

, ,

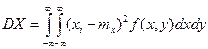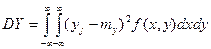(6.23)

если - непрерывная система случайных величин.

Дисперсии DX и DY характеризуют рассеяние (разброс) случайной точки и в направлении осей Ох и Оу вокруг точки 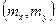на плоскости Оху - центра рассеяния.

Математические ожидания m_х и m_у являются частными случаями начального момента 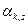порядка k + s системы , определяемого равенством

,

,

.

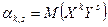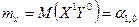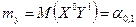Дисперсии DX и DY являются частными случаями центрального момента 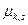порядка k + s системы , определяемого равенством

,

,

.

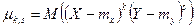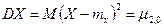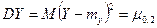Математическое ожидание случайной величины 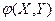, являющейся функцией компонент X и Y двумерной случайной величины находится, аналогично, по формулам:

- для непрерывного случая

,

(6.24)

- для дискретного случая

.

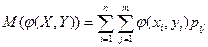(6.25)

Начальный момент II порядка 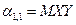часто встречается в приложениях. Вычисляется по формуле

- для дискретных случайных величин

,

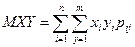(6.26)

- для непрерывных случайных величин

.

(6.27)