Линейная парна регрессия

Уравнение регрессии (К2) будем искать в виде линейного уравнения

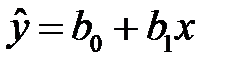. (К4)

Таким образом, аппроксимирующая функция 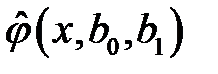является линейной, то есть 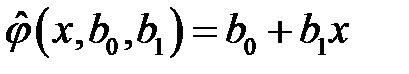. В таком случае, получаем выражения для частных производных

,

.

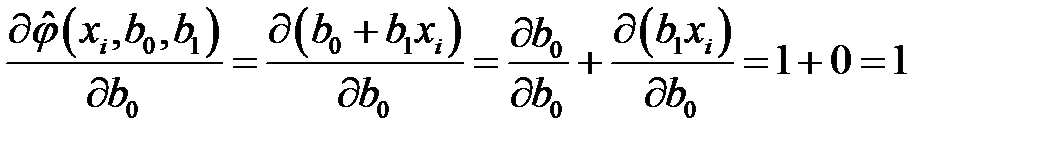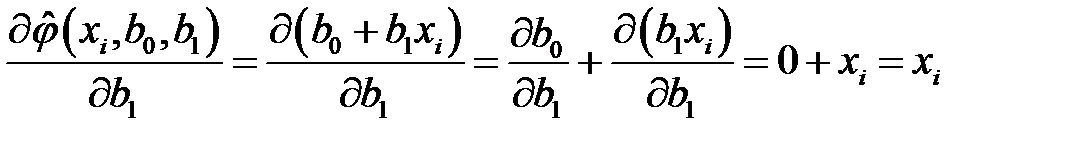Подставляя эти производные в систему (К3), получим

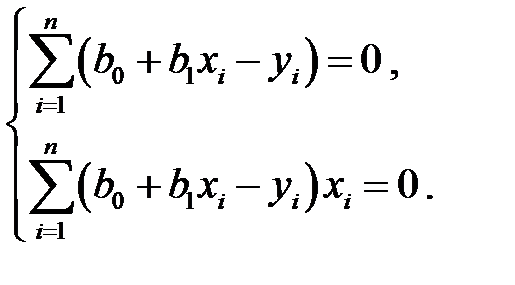(К5)

Очевидно

,

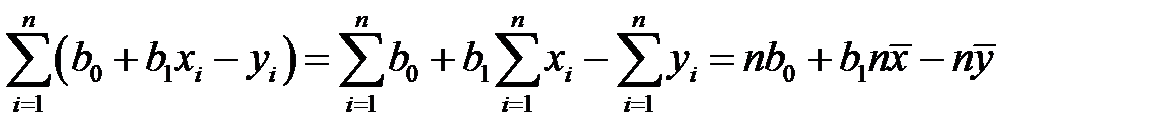ибо

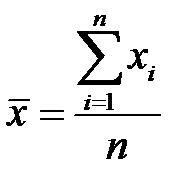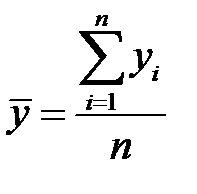, (К6)

и

,

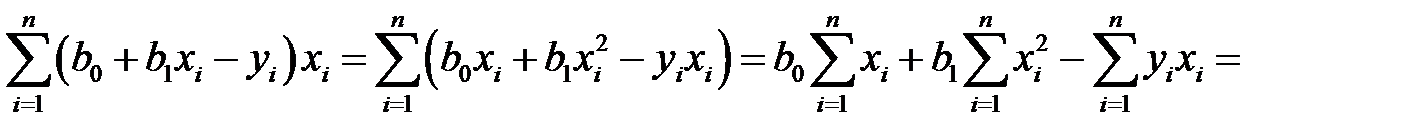
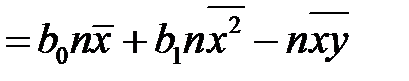ибо

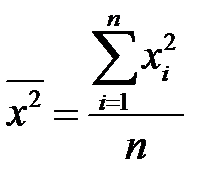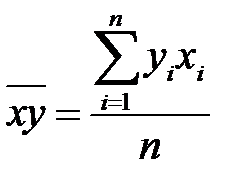, . (К7)

В таком случае, система (К5) примет вид

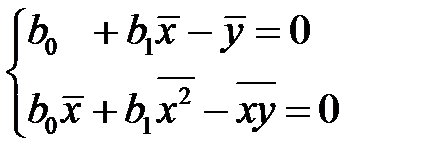
из которой приходим к системе

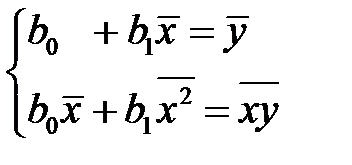(К8)

Решаем данную систему методом Крамера.

,

, .

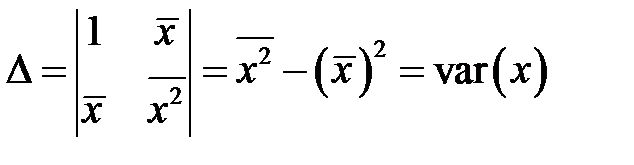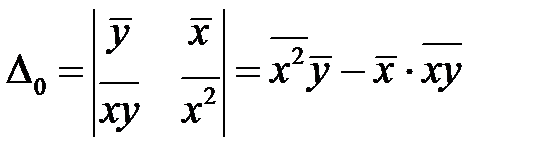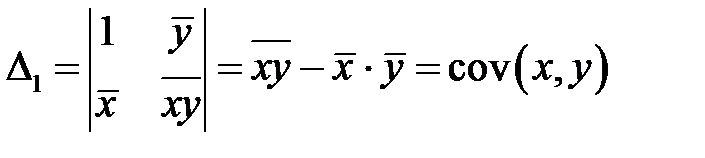По формулам Крамера, обнаруживаем

, .

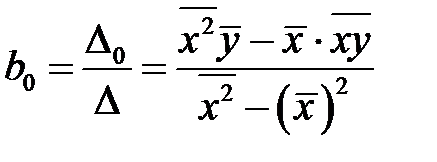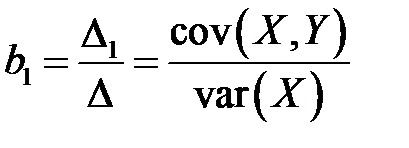Таким образом, получаем выражения для коэффициентов

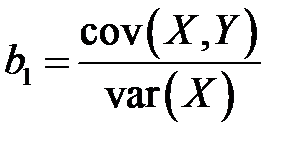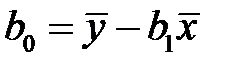, . (К9)

Коэффициент 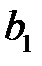называется выборочным коэффициентом регрессии (или просто коэффициентом регрессии) 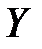по .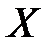

Коэффициент регрессии 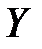по 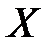показывает, на сколько единиц в среднем изменяется переменная 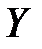при увеличении переменной 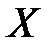на одну единицу.

Здесь 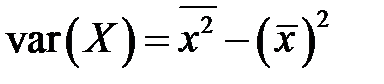– выборочная дисперсия переменной 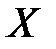. Очевидно учитывая равенства (К6) и (К7), получим

,

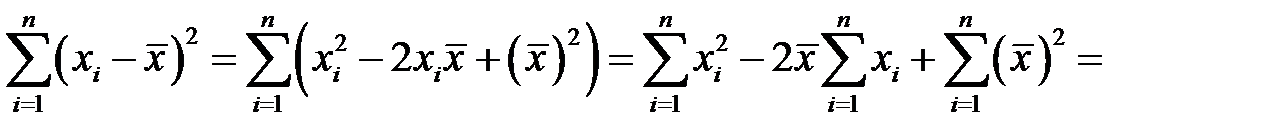
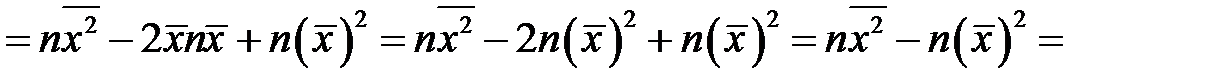
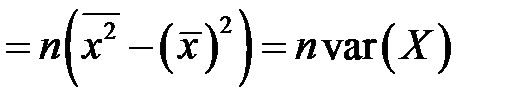что влечет равенство

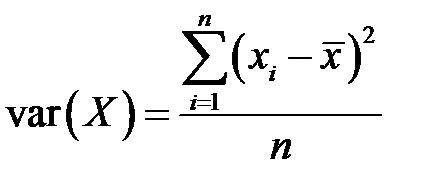. (К10)

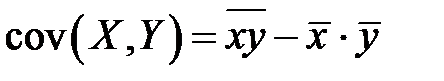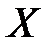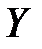Кроме того, – выборочный корреляционный момент или выборочная ковариация переменных и . Очевидно учитывая равенства (К6) и (К7), находим

,

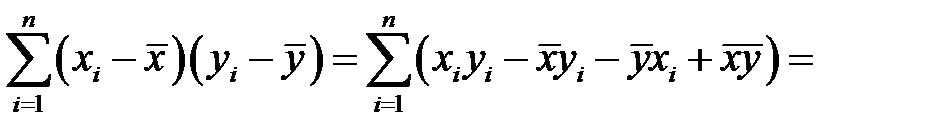
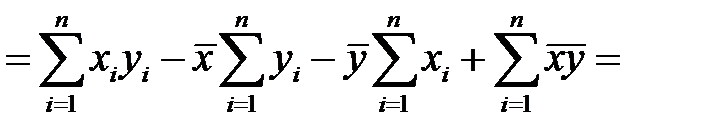
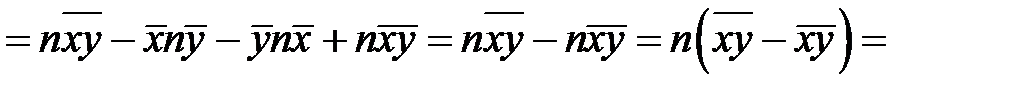
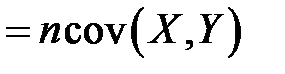что влечет равенство

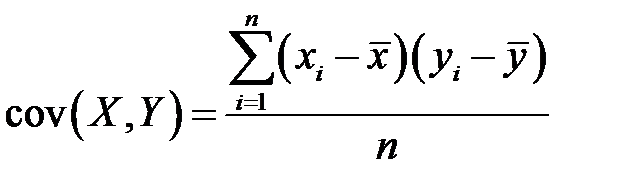. (К11)