Основные положения регрессионного анализа

В силу воздействия неучтенных случайных факторов и причин отдельные наблюдения переменной 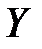будут в большей или меньшей мере отклоняется от функции регрессии 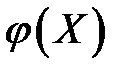. В этом случае уравнение взаимосвязи двух переменных (парная регрессионная модель) может быть представлено в виде

,

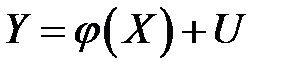где 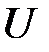– случайная величина (случайный член), характеризующая отклонение от функции регрессии. Эту переменную будем называть возмущением, либо ошибкой. Таким образом, в регрессионной модели зависимая переменная 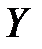есть некоторая функция 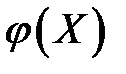с точностью до случайного возмущения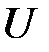

Рассмотрим линейный регрессионный анализ, для которого функция 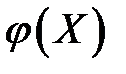линейная относительно оцениваемых параметров .

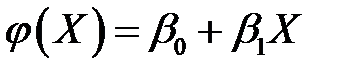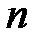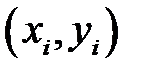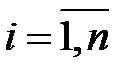Предположим, что для оценки параметров линейной регрессии взята выборка, содержащая пар значений переменных , где . Результаты наблюдений и 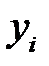можно рассматривать как значения случайных величин 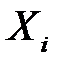и 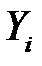имеющих такое распределение как случайные величины 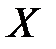и 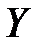соответственно. В этом случае линейная парная регрессионная модель имеет вид

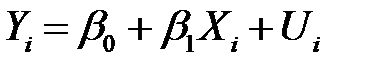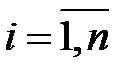, . (К14)

Отметим основные предпосылки регрессионного анализа.

(РА1). В модели (К14) возмущение 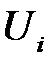, 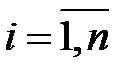(или зависимая переменная 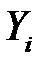) есть величина случайная, а объясняющая переменная 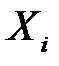– величина не случайная.

(РА2). Математическое ожидание возмущения 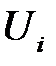, 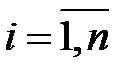равно нулю

(К15)

или математическое ожидание зависимой переменной 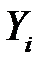равно линейной функции регрессии

.

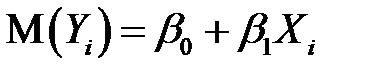(РА3) (условие гомоскедастичности или равноизменчивости возмущения (зависимой переменной)). Дисперсия возмущения 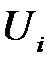(или зависимой переменной 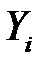) постоянна для любого 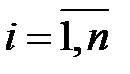, то есть

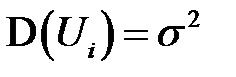(К16)

или

.

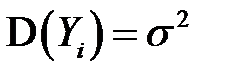(РА4) (условие некоррелированности). Для любых 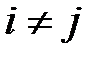возмущения 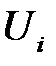и 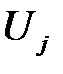удовлетворяют условию

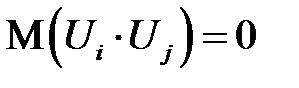. (К17)

(РА5). Возмущение 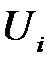(или зависимая переменная 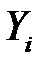) являются нормально распределенными случайными величинами.

В этом случае модель (К14) называется классической нормальной линейной регрессионной моделью (Classical Normal Linear Regression model).

Для получения уравнения регрессии достаточно предпосылок (1) – (4). Требование выполнения предпосылки (5) необходимо для оценки точности уравнения регрессии и его параметров.

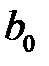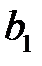Оценкой модели (К14) по выборке является уравнение регрессии (К4). Параметры этого уравнения и определяются на основе метода наименьших квадратов и вычисляются по формулам (К9).

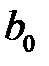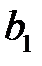Теорема(Гаусса – Маркова). Если регрессионная модель (К14) удовлетворяет предпосылкам (1) – (4), то оценки и , определенные по формулам (К9), имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Таким образом, оценк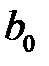и и 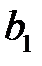в определенном смысле являются наиболее эффективными линейными оценками параметров 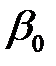и .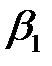

Воздействие неучтенных случайных факторов и ошибок наблюдений в модели (К14) определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии 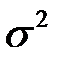. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия

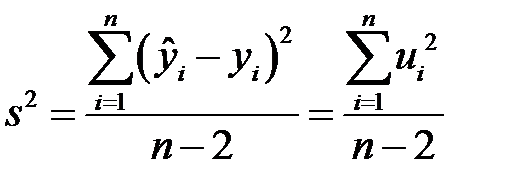, (К18)

где

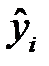– групповая средняя, найденная по уравнению регрессии (К4),

– выборочная оценка возмущения 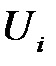или остаток регрессии.

Напомним, что в математической статистике для получения несмещенной оценки дисперсии случайной величины соответствующую сумму квадратов отклонений от средней делят не на число наблюдений 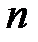, а на число степеней свободы 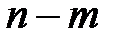, равное разности между числом независимых наблюдений случайной величины 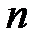и числом связей, ограничивающих свободу их изменения, то есть число 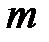уравнений, связывающих эти наблюдения. Поэтому в знаменателе выражения (К18) стоит число степеней свободы 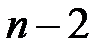, так как две степени свободы теряются при определении двух параметров прямой из системы уравнений (К5).