Функциональная, статистическая и корреляционная зависимости

Функциональной зависимостью называется соответствие каждому значению одной переменной вполне определенного значения другой.

Статистической (или стохастической, вероятностной) зависимостью называется соответствие каждому значению одной переменной (случайной величины) определенного (условного) распределения другой переменной (случайной величины).

Возникновение понятия статистической связи обуславливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками.

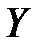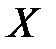В силу неоднозначности статистической зависимости между и для исследователя, в частности, представляет собой интерес усредненная по 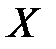схема зависимости, то есть закономерность в измерении условного математического ожидания[1] 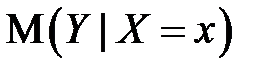в зависимости от .

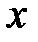Корреляционной зависимостью называется соответствие каждому значению 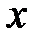переменной 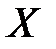условного математического ожидания 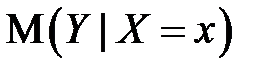случайной величины .

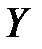Корреляционная зависимость может быть представлена в виде

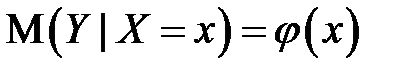. (К1)

Уравнение (К1) называется уравнением регрессии, а функция 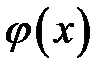– функцией регрессии.

Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной 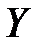при условии, что переменная 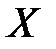примет значение 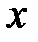, то есть 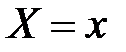. В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений 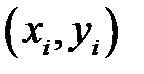ограниченного объема 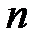. В этом случае, речь может идти об оценке (приближенном выражении, аппроксимации) по выборке функции регрессии. Такой оценкой является выборочное уравнение (линия, кривая) регрессии.

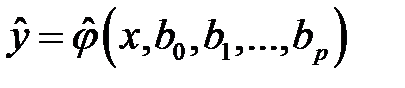, (К2)

где 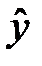– условная (групповая) средняя переменной 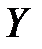при фиксированном значении переменной 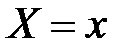, , 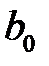, 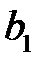…, 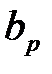– параметры кривой.

Уравнение (К2) называется выборочным уравнением регрессии. При правильно определенной аппроксимирующей функции 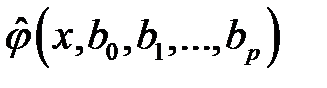с увеличением объема выборки 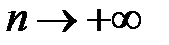она будет сходится по вероятности к функции регрессии .

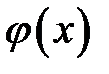2. Метод наименьших квадратов

Для нахождения неизвестных параметров 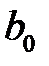, , 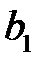…, 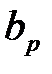применяется метод наименьших квадратов. Согласно методу наименьших квадратов неизвестные параметры 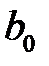, , 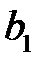…, 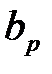выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений 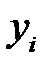от значений 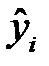, найденных по уравнению регрессии (К2) 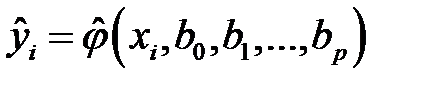, , 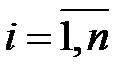была минимальной

.

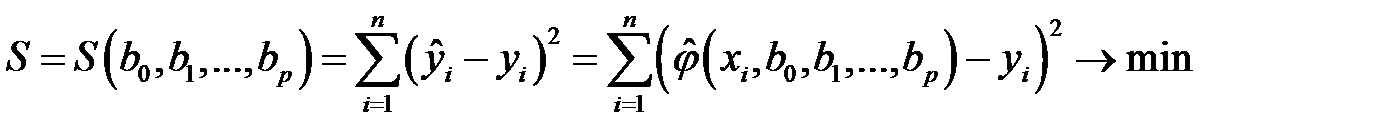Необходимым условием экстремума функции 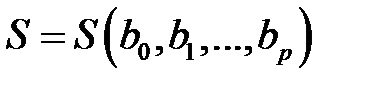переменных 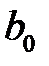, , 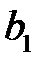…, 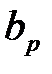является равенство нулю ее частных производных

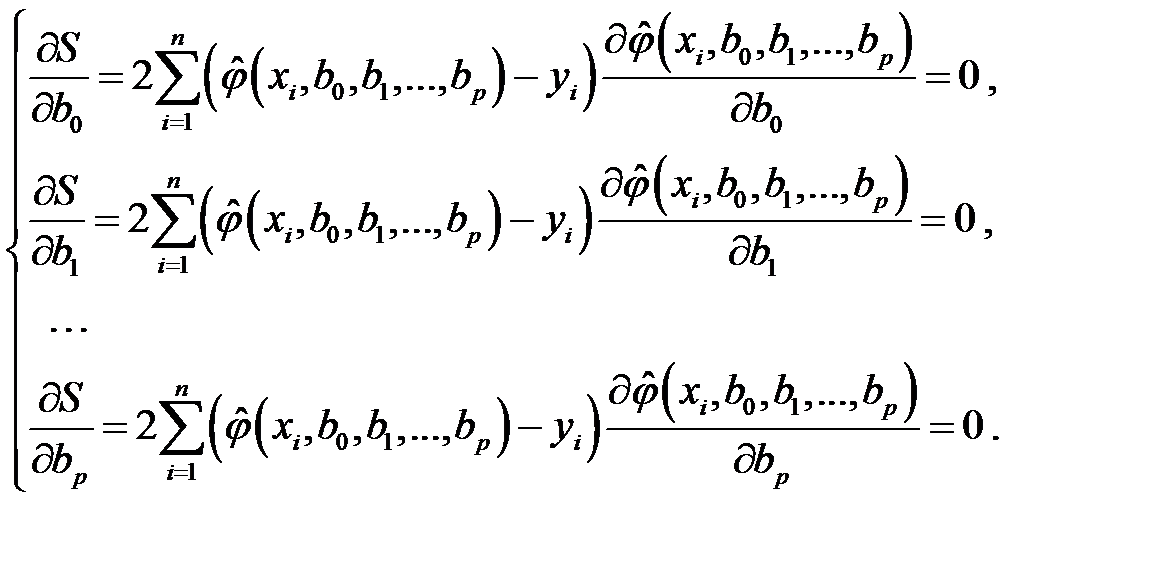(К3)

После преобразования получим систему для определения параметров линейной регрессии.