Множественный регрессионный анализ
Математическое ожидание и дисперсия случайной матрицы. Ковариантная матрица случайного вектора.
Для матрицы 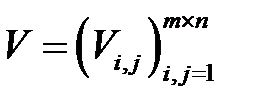 случайных величин
случайных величин 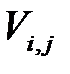 ,
, 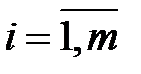 ,
, 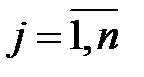 числовую матрицу их математических ожиданий
числовую матрицу их математических ожиданий 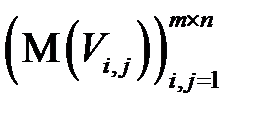 (соотв. дисперсий
(соотв. дисперсий 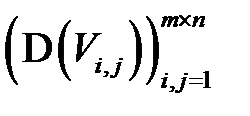 ) будем называть математическим ожиданием (соотв. дисперсией) матрицы
) будем называть математическим ожиданием (соотв. дисперсией) матрицы 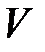 и обозначать
и обозначать 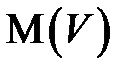 (соотв.
(соотв. 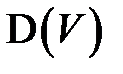 ), то есть
), то есть
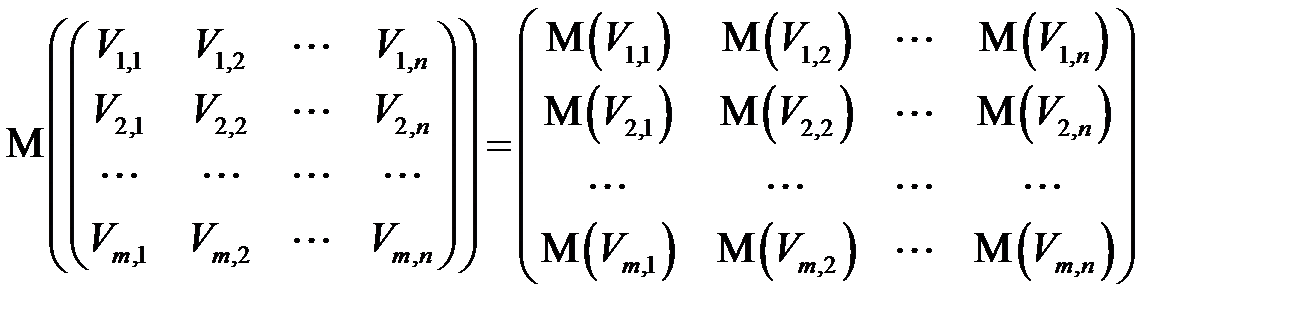
и
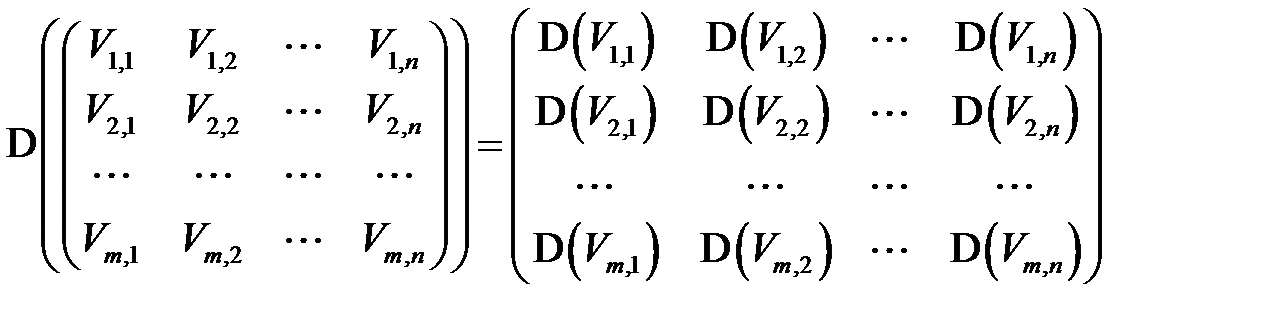 .
.
Для вектора 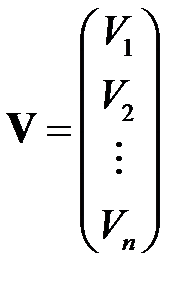 матрица
матрица
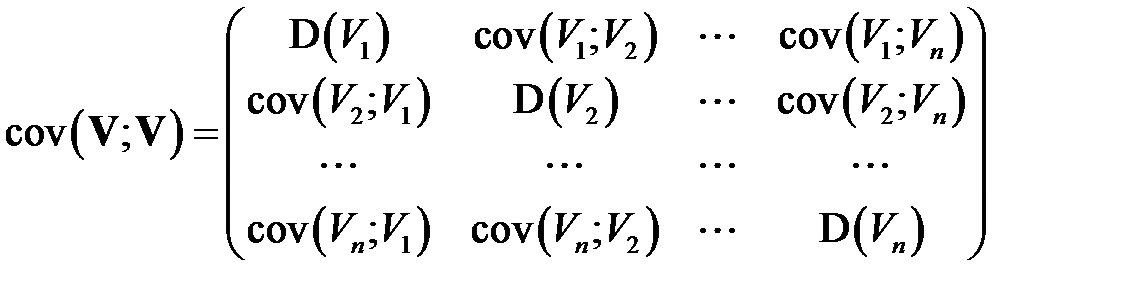 , (КОВ_1)
, (КОВ_1)
где
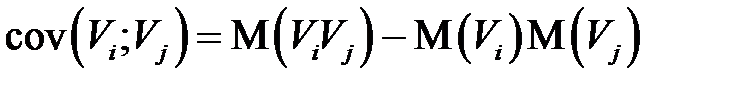 (КОВ_2)
(КОВ_2)
называется ковариантной матрицей вектора 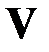 .
.
Поскольку вектор  является матрицей размерности
является матрицей размерности 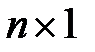 , то транспонированная матрица
, то транспонированная матрица 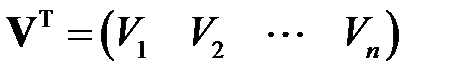 представляет собой матрицу размерности
представляет собой матрицу размерности 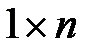 . Их произведение матриц
. Их произведение матриц 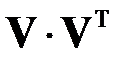 является матрицей размерности
является матрицей размерности 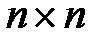
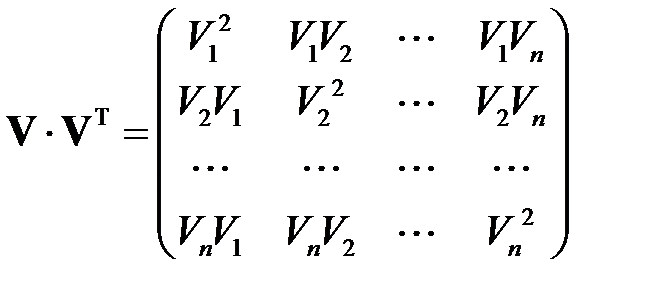 .
.
В таком случае, по определению математических ожиданий
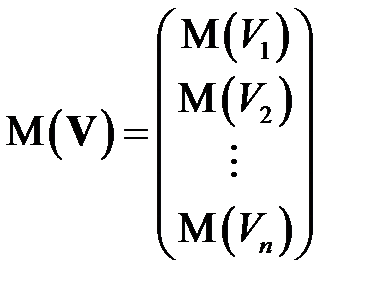 ,
, 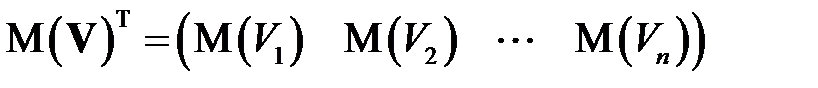 ,
,
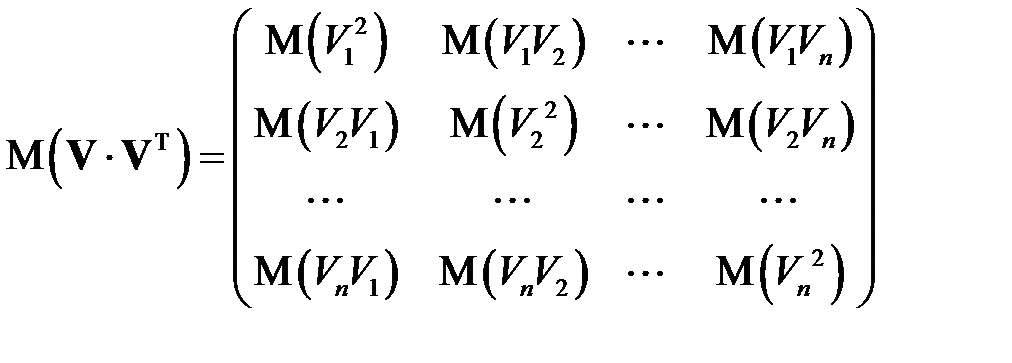 ,
,
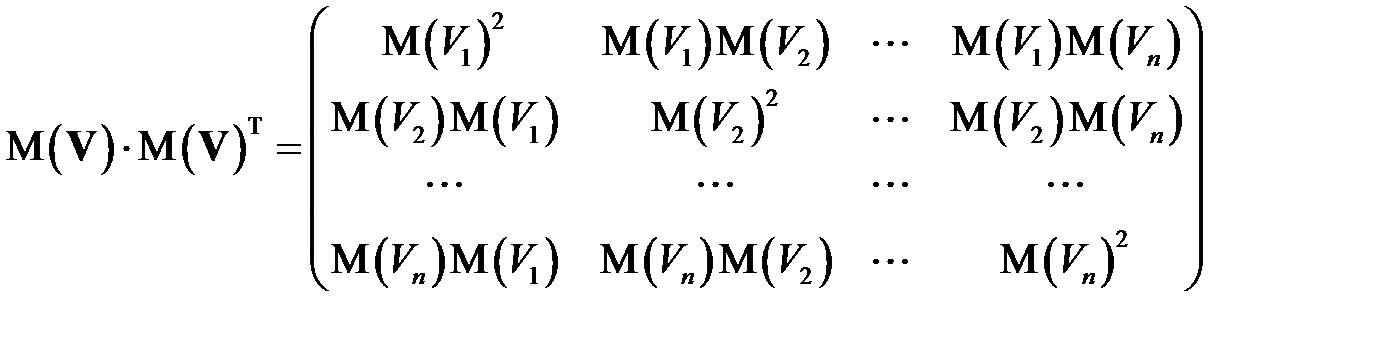 .
.
В таком случае, имеем
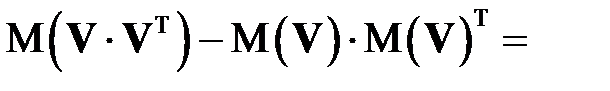
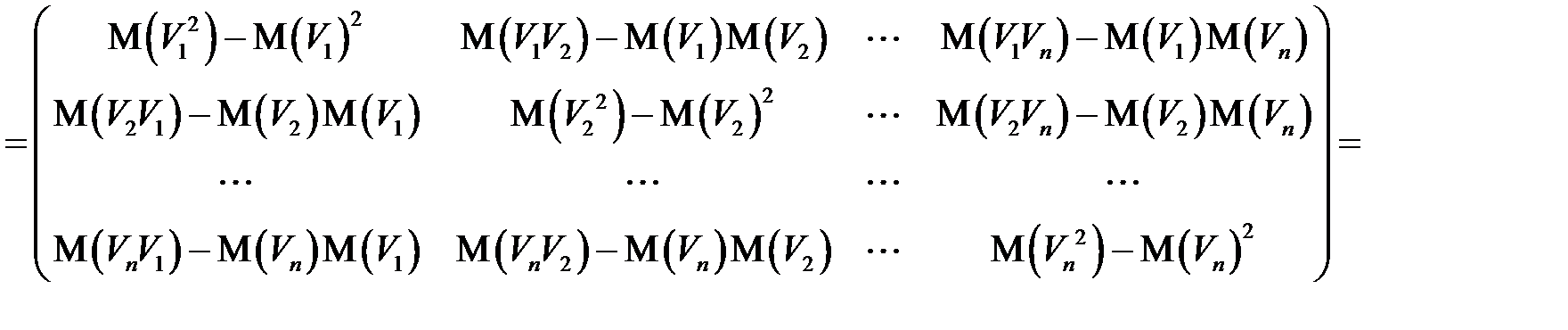
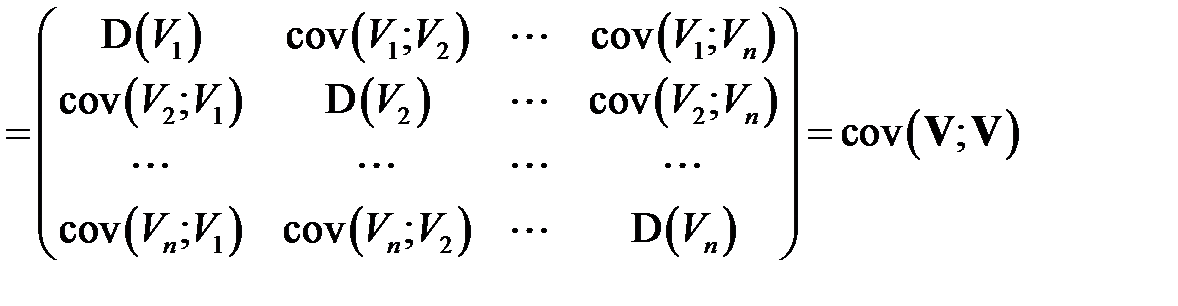 .
.
Тем самым доказано равенство
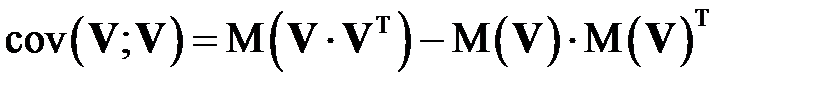 . (КОВ_3)
. (КОВ_3)
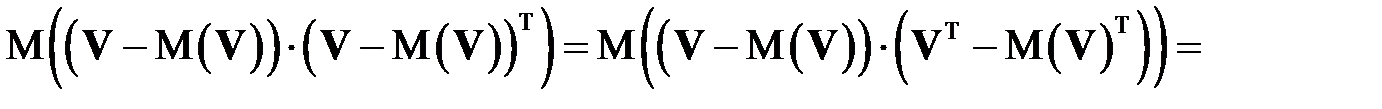
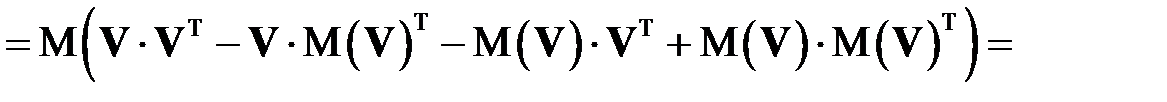
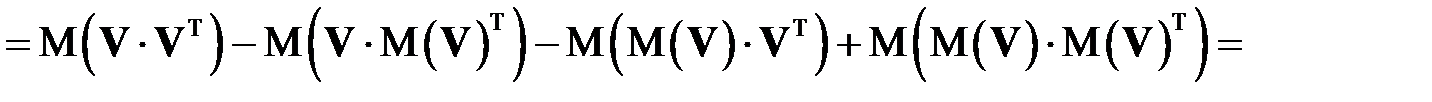
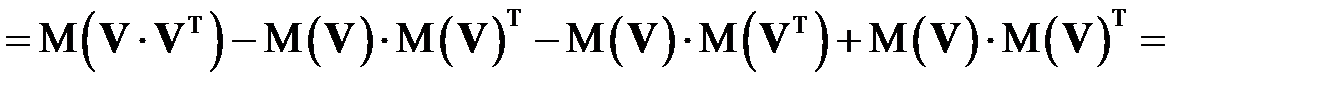
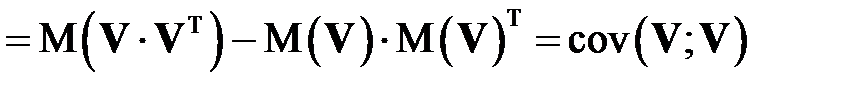 .
.
9. Классическая нормальная линейная модель множественной регрессии
Экономические явления, как правило, определяются большим числом одновременно и совокупно действующих факторов. В связи с этим часто возникает задача исследования зависимости одной зависимой переменной 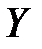 от нескольких объясняющих переменных
от нескольких объясняющих переменных 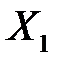 ,
, 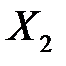 , …,
, …, 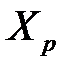 . Эта задача решается с помощью множественного регрессионного анализа.
. Эта задача решается с помощью множественного регрессионного анализа.
Обозначим 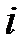 -ое наблюдение зависимой переменной
-ое наблюдение зависимой переменной 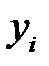 , а объясняющих переменных –
, а объясняющих переменных – 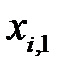 ,
, 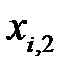 , …,
, …, 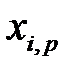 . Тогда модель множественной линейной регрессии можно представить в виде
. Тогда модель множественной линейной регрессии можно представить в виде
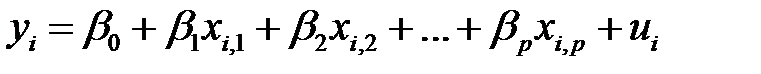 ,
, 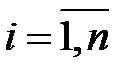 , (М1)
, (М1)
где 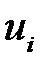 удовлетворяет приведенным выше предпосылкам (РА1) – (РА5).
удовлетворяет приведенным выше предпосылкам (РА1) – (РА5).
Модель (М1), в которой зависимая переменная 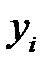 , возмущения
, возмущения 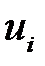 и объясняющие переменные
и объясняющие переменные 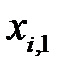 ,
, 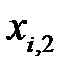 , …,
, …, 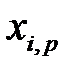 удовлетворяют предпосылкам (РА1) – (РА5) регрессионного анализа и, кроме того, предпосылке (РА6) о не вырожденности матрицы (независимых столбцов) значений объясняющих переменных, называется классической нормальной линейной моделью множественной регрессии (Classic Normal Linear Multiple Regression model).
удовлетворяют предпосылкам (РА1) – (РА5) регрессионного анализа и, кроме того, предпосылке (РА6) о не вырожденности матрицы (независимых столбцов) значений объясняющих переменных, называется классической нормальной линейной моделью множественной регрессии (Classic Normal Linear Multiple Regression model).
Включение в регрессионную модель новых объясняющих переменных усложняет получаемые формулы и вычисления. Это приводит к целесообразности матричных обозначений. Матричное описание регрессии облегчает как теоретические концепции анализа, так и необходимые расчетные процедуры.
Пусть
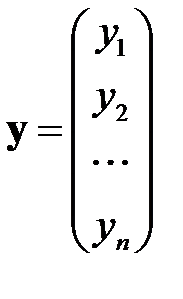
матрица-столбец, или вектор, значений зависимой переменной размерности 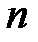 ;
;
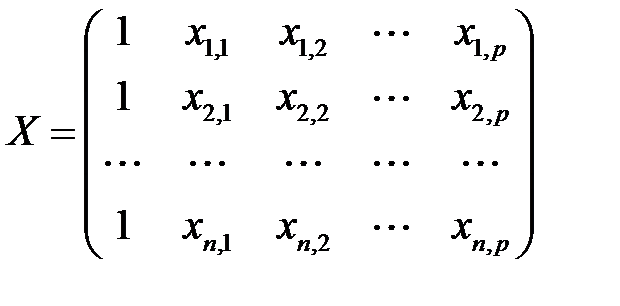
матрица значений объясняющих переменных, или матрицы плана, размерности 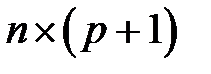 ;
;
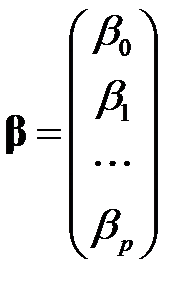
матрица-столбец, или вектор, параметров размерности 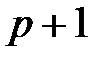 ;
;
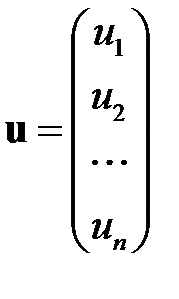
матрица-столбец, или вектор, возмущений (случайных ошибок, остатков) размерности 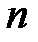 . Тогда в матричной форме модель (М1) принимает вид
. Тогда в матричной форме модель (М1) принимает вид
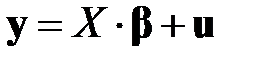 . (М2)
. (М2)
В таком случае, уравнение регрессии в матричной форме принимает вид
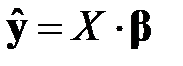 . (М3)
. (М3)
Вектор случайных ошибок
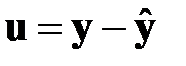 . (М4)
. (М4)
10. Оценка параметров классической регрессионной модели методом наименьших квадратов
Очевидно
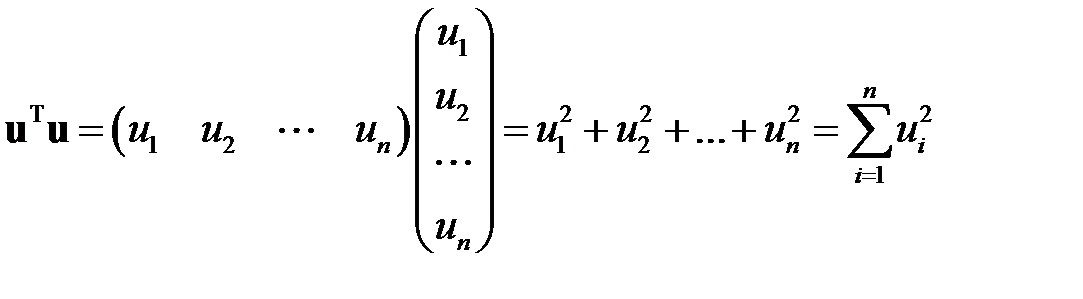 .
.
В таком случае, учитывая равенства (М2) – (М4), сумма квадратов отклонений примет вид
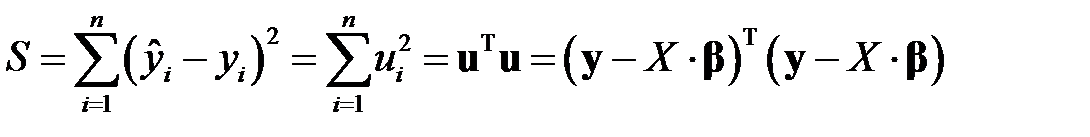 .
.
Поскольку при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, то есть
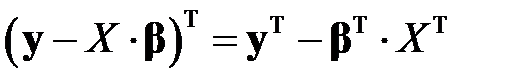 ,
,
то
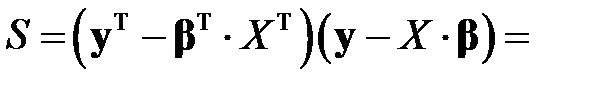
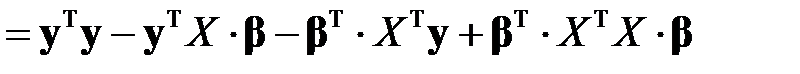 .
.
Произведение 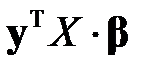 есть матрица размерности
есть матрица размерности
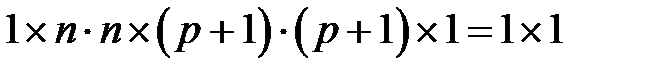 ,
,
а потому не меняется при транспонировании, то есть
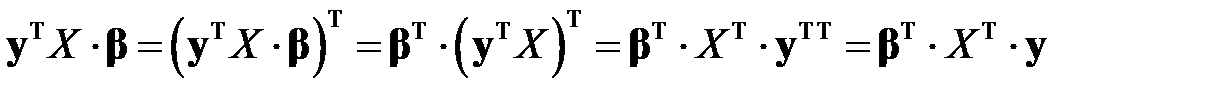 .
.
В таком случае, приходим к равенству
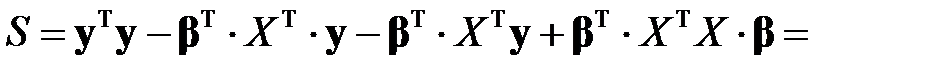
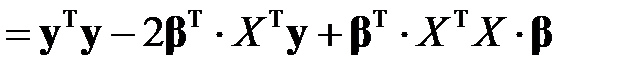 .
.
Для оценки вектора неизвестных параметров 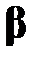 применим метод наименьших квадратов, суть которого состоит в том, что вектор оценок
применим метод наименьших квадратов, суть которого состоит в том, что вектор оценок
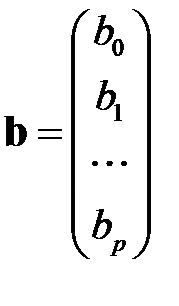
вектора неизвестных параметров 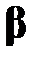 ищется как решение оптимизационной модели
ищется как решение оптимизационной модели
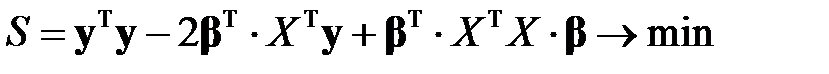 .
.
На основании необходимого условия экстремума функции нескольких переменных 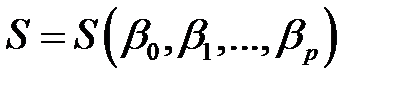 частные производные приравниваются нулю
частные производные приравниваются нулю
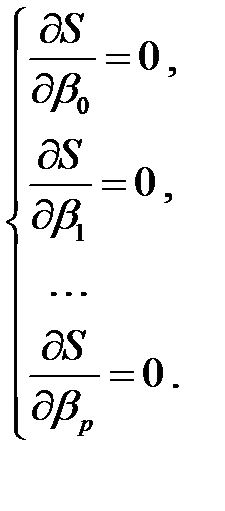 (М5)
(М5)
Вводя в рассмотрение вектор
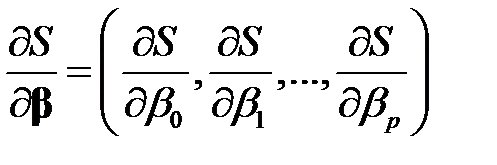 ,
,
система (М5) запишется в равносильной векторной форме
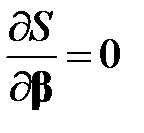 . (М6)
. (М6)
Утверждение(свойства вектора частных производных). (а) Для вектора 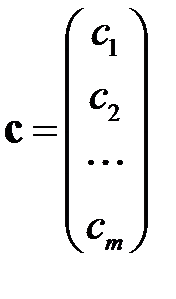 выполняется равенство
выполняется равенство
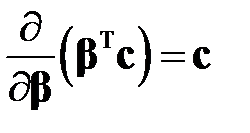 , (М7)
, (М7)
(б) для симметрической матрицы 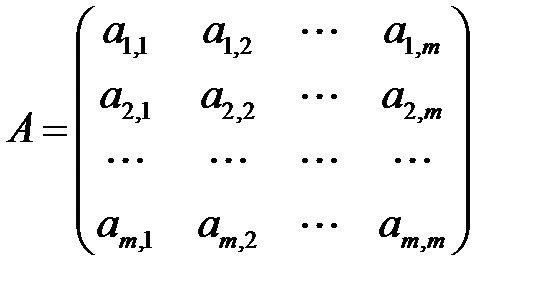 выполняется равенство
выполняется равенство
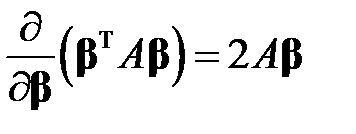 . (М8)
. (М8)
Доказательство. (а) Очевидно
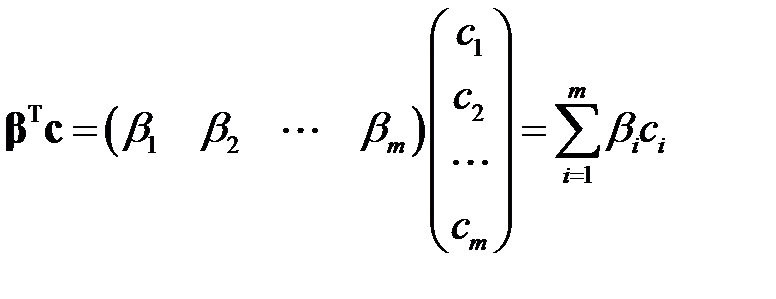 .
.
В таком случае,
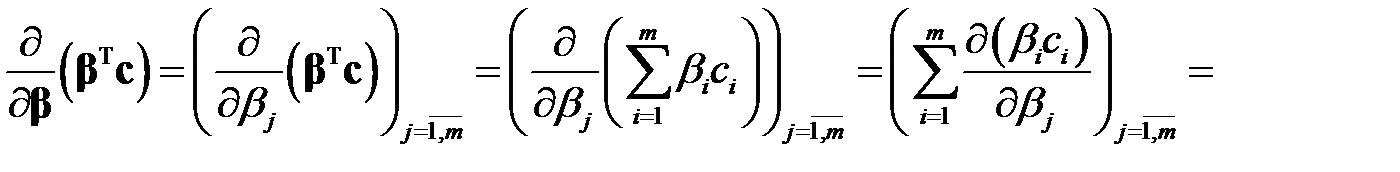
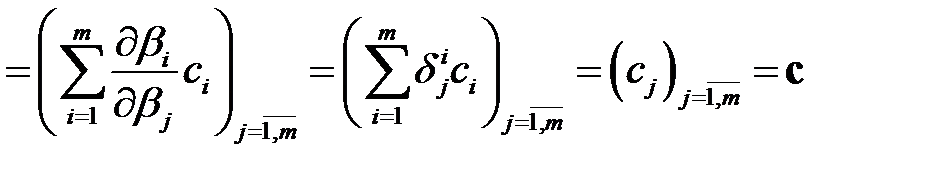 .
.
(б) Понятно, что
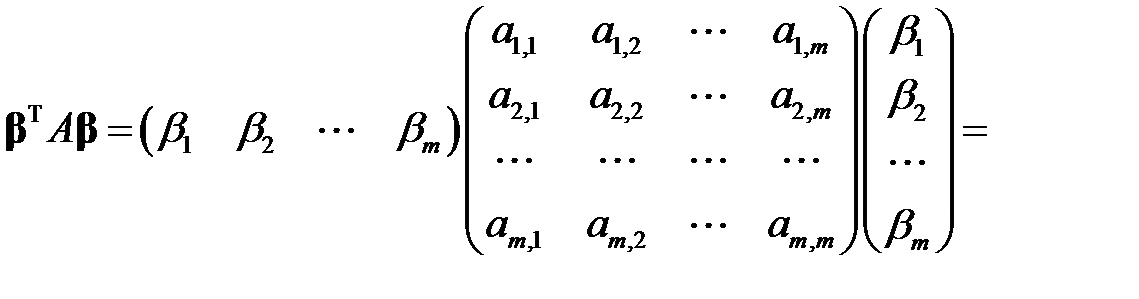
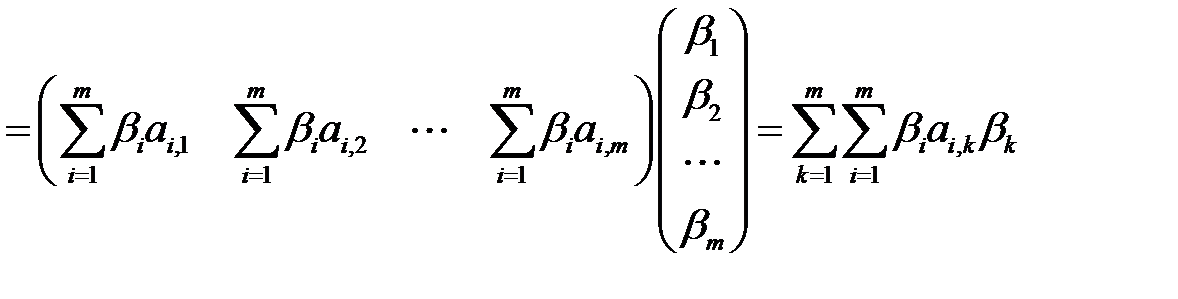 .
.
С учетом данного равенства, находим
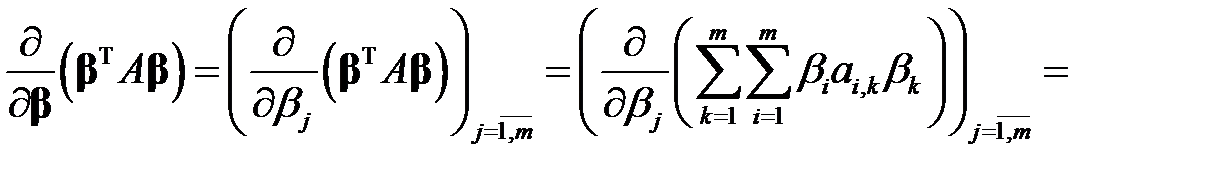
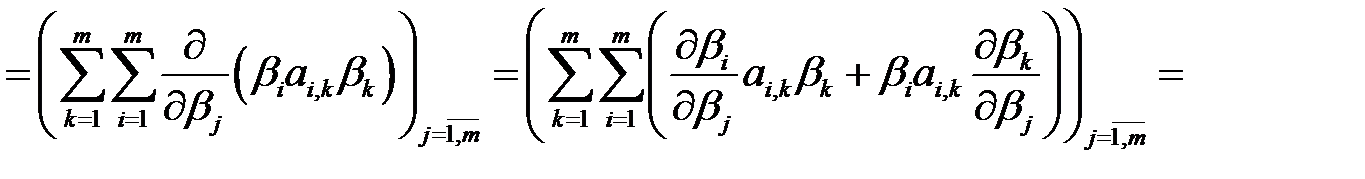
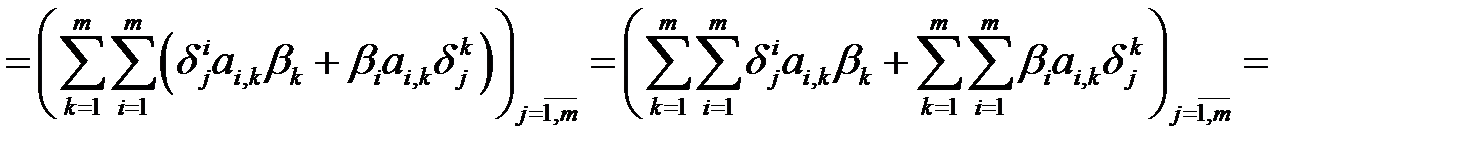
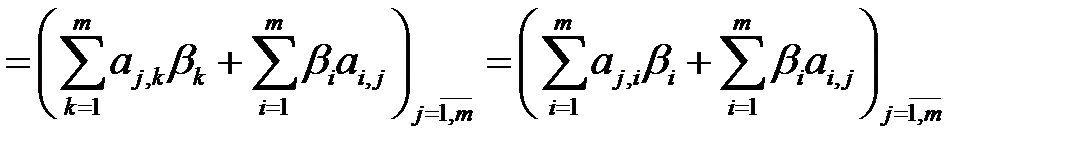 .
.
Учитывая симметричность матрицы 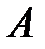 , то есть равенства
, то есть равенства 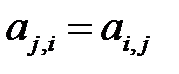 , получим
, получим
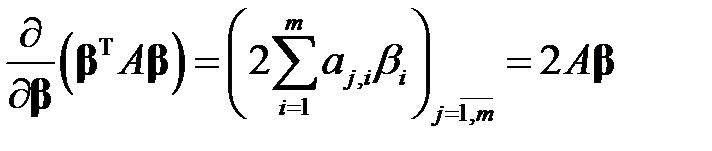 ,
,
что и требовалось доказать.
Матрица 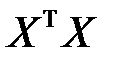 симметрическая, ибо
симметрическая, ибо
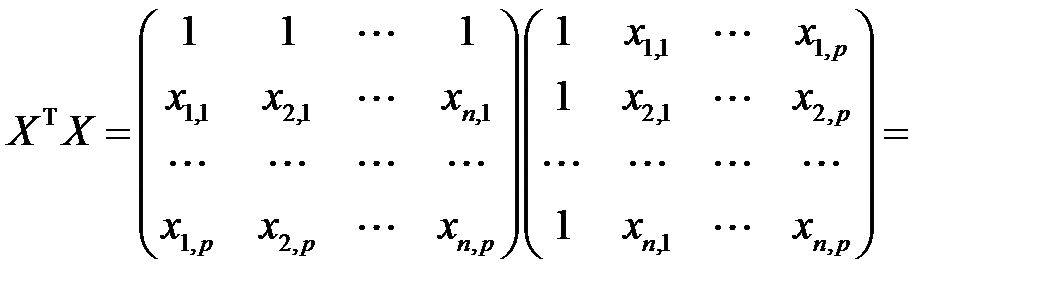
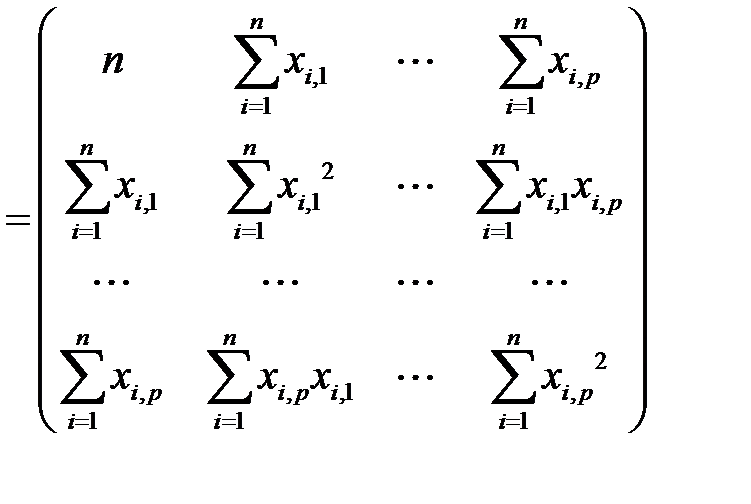 . (М9)
. (М9)
В таком случае, учитывая свойства (а) и (б) вектора частных производных, получим
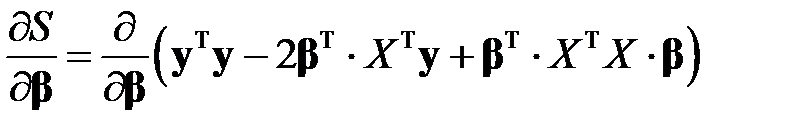
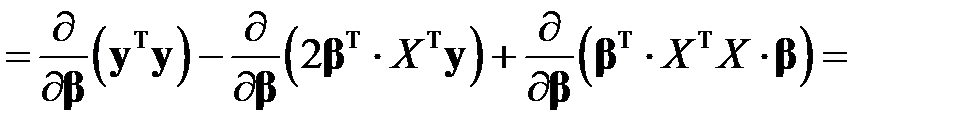
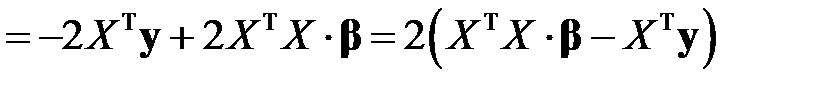 .
.
В таком случае, равенство (М6) равносильно системе
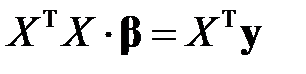 . (М10)
. (М10)
Таким образом, искомый вектор оценок 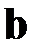 является решением системы уравнений (М10), то есть верно равенство
является решением системы уравнений (М10), то есть верно равенство
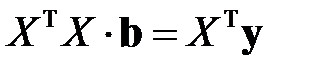 , (М11)
, (М11)
где
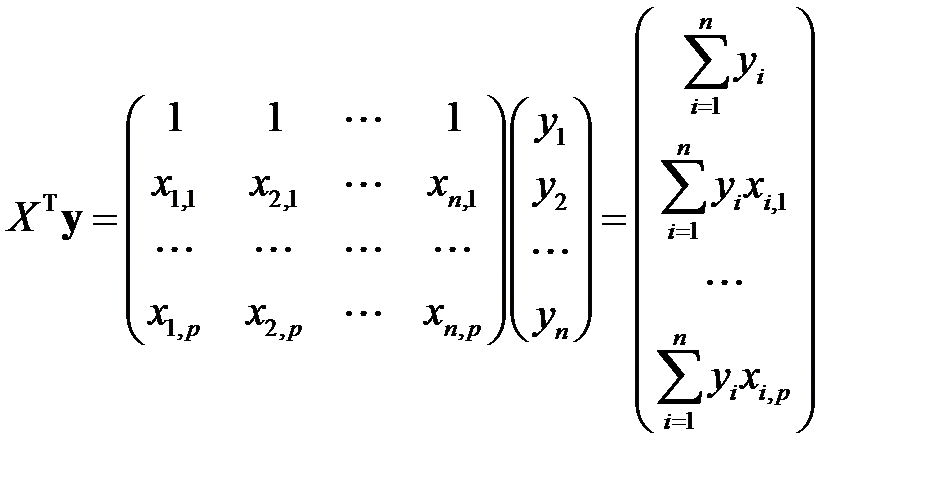 . (М12)
. (М12)
Для решения матричного уравнения (М11) необходимо ввести предположение об обратимости матрицы 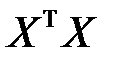 . Последнее равносильно равенству
. Последнее равносильно равенству 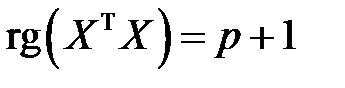 . Из матричной алгебры известно, что
. Из матричной алгебры известно, что 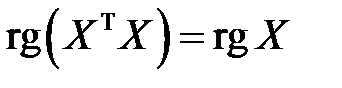 ., приходим к выражению для вектора оценок коэффициентов
., приходим к выражению для вектора оценок коэффициентов
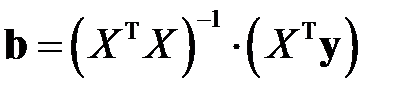 . (М13)
. (М13)
Пример 1.1. Имеются следующие данные о сменной добыче угля на одного рабочего  в тоннах, мощности пласта
в тоннах, мощности пласта  в метрах и уровне механизации работ
в метрах и уровне механизации работ 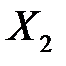 в %, характеризующие процесс добычи угля в десяти шахтах.
в %, характеризующие процесс добычи угля в десяти шахтах.
№ п/п, 
| Сменная добыча угля на одного рабочего, т 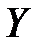
| Мощность пласта, м 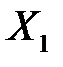
| Уровень механизации работ, % 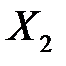
|
Предполагая, что между переменными 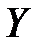 ,
, 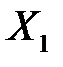 и
и 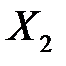 существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии
существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии 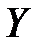 по
по 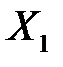 и
и 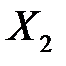 ).
).
Решение.
Уравнение регрессии ищем в виде
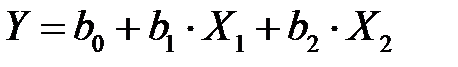 .
.
Для нахождения вектора оценок
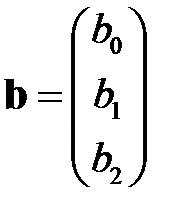
строим матрицы
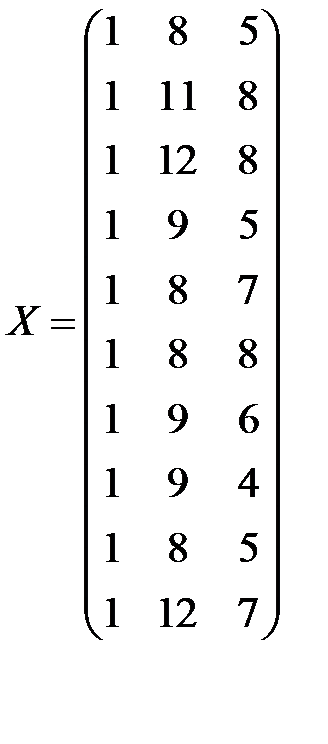
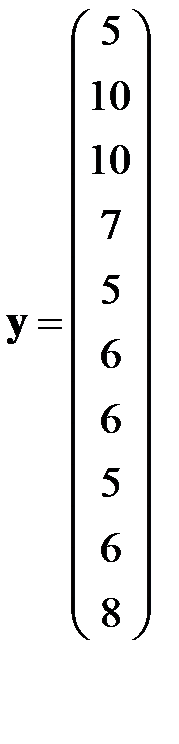
 .
.
По правилу умножения матриц, получим
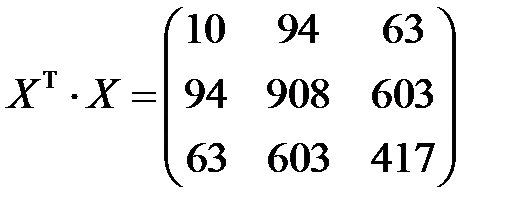 ,
, 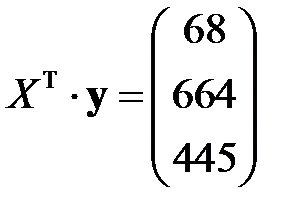 .
.
По формуле 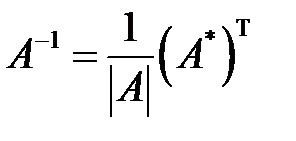 находим обратную матрицу
находим обратную матрицу
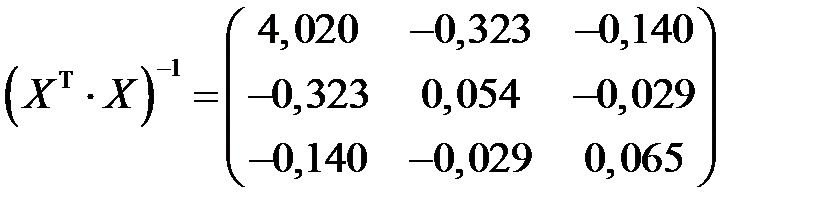 .
.
Теперь получаем вектор оценок
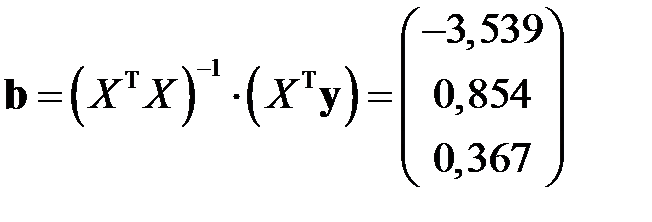 ,
,
то есть
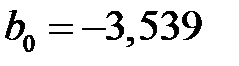 ,
, 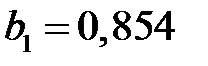 ,
, 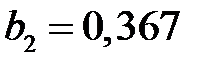 .
.
Таким образом, уравнение регрессии
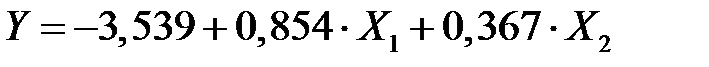 .
.
11. Ковариантная матрица и ее выборочная оценка
Учитывая (М9) и (М12), матричное равенство (М11) запишем в виде системы скалярных равенств
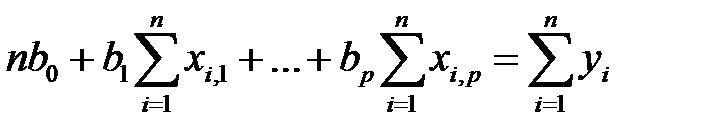 ,
,
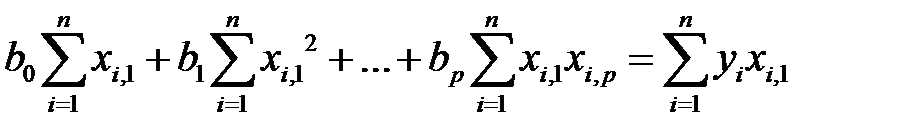
. . . . . . . . . . . (М21)
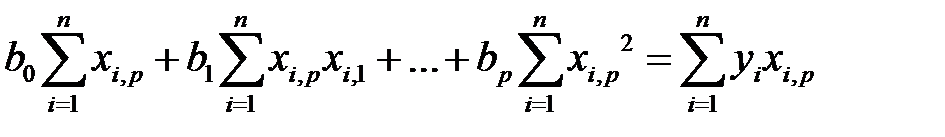 .
.
Деля каждое уравнение системы на 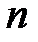 , и учитывая определение средних величин
, и учитывая определение средних величин
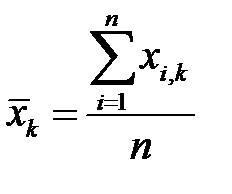 ,
, 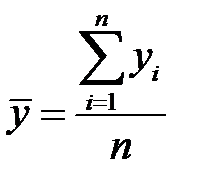 ,
,
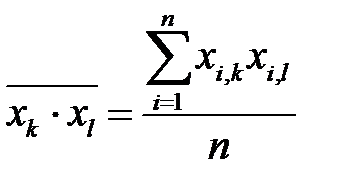 ,
, 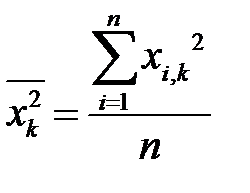 ,
, 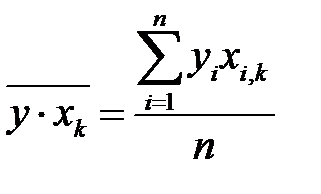 ,
,
получим систему
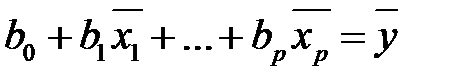 ,
,
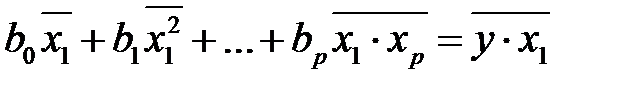 ,
,
. . . . . . . . . .
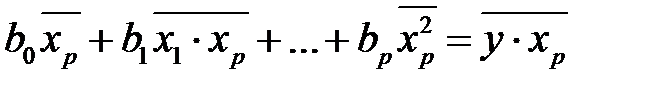 .
.
Умножим первое равенство на 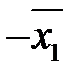 и прибавим ко второму; обнаруживаем
и прибавим ко второму; обнаруживаем
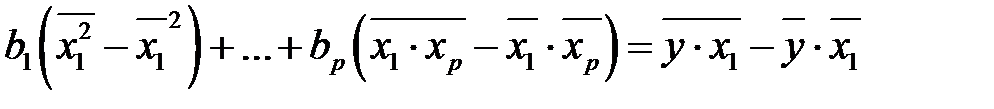 .
.
Подобным образом поступает для каждого последующего уравнения. Умножим первое равенство на 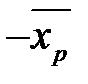 и прибавим к последнему. Получаем
и прибавим к последнему. Получаем
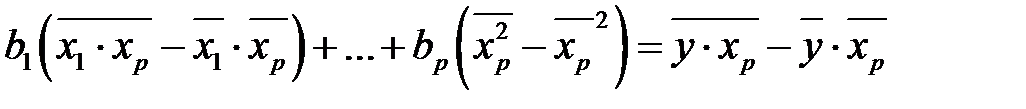 .
.
Так как
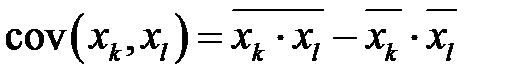 ,
,
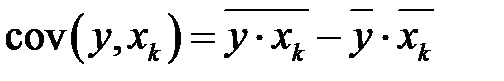 ,
,
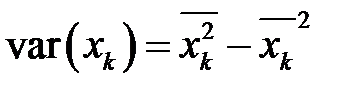 ,
,
получим систему
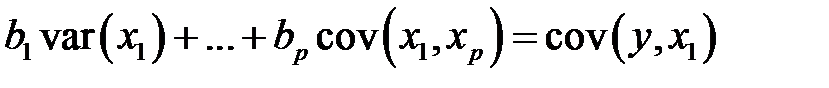 ,
,
. . . . . . . . . . . (М22)
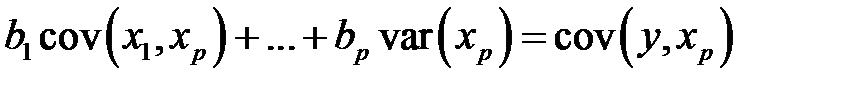 .
.
Поскольку система (М22) имеет размерность на единицу меньшую размерности системы (М11), то предпочтительнее сначала решить систему (М22), а затем найти 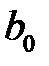 из равенства
из равенства
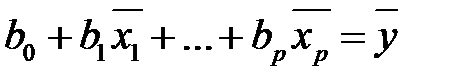 . (М23)
. (М23)
Пример 1.2. Имеются следующие данные о сменной добыче угля на одного рабочего  в тоннах, мощности пласта
в тоннах, мощности пласта 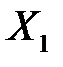 в метрах и уровне механизации работ
в метрах и уровне механизации работ 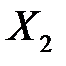 в %, характеризующие процесс добычи угля в десяти шахтах (см. пример 1.1). Предполагая, что между переменными
в %, характеризующие процесс добычи угля в десяти шахтах (см. пример 1.1). Предполагая, что между переменными 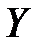 ,
, 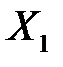 и
и 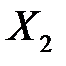 существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии
существует линейная корреляционная зависимость, найти ее аналитическое выражение (уравнение регрессии 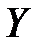 по
по 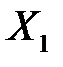 и
и 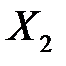 ).
).
Решение. Для нахождения матриц 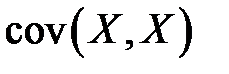 и
и 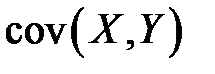 строим таблицы
строим таблицы
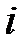
| 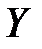
| 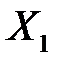
| 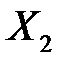
| 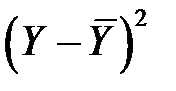
| 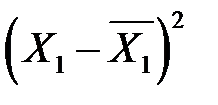
| 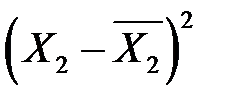
| 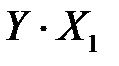
| 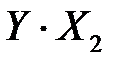
| 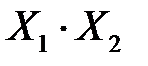
|
| 3,24 | 1,96 | 1,69 | |||||||
| 10,24 | 2,56 | 2,89 | |||||||
| 10,24 | 6,76 | 2,89 | |||||||
| 0,04 | 0,16 | 1,69 | |||||||
| 3,24 | 1,96 | 0,49 | |||||||
| 0,64 | 1,96 | 2,89 | |||||||
| 0,64 | 0,16 | 0,09 | |||||||
| 3,24 | 0,16 | 5,29 | |||||||
| 0,64 | 1,96 | 1,69 | |||||||
| 1,44 | 6,76 | 0,49 | |||||||
| Σ | 33,6 | 24,4 | 20,1 | ||||||
| М | 6,8 | 9,4 | 6,3 | 3,36 | 2,44 | 2,01 | 66,4 | 44,5 | 60,3 |
Отсюда уже получаем
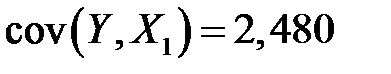 ,
, 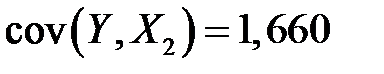 ,
, 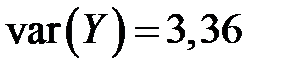
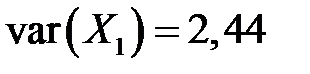 ,
, 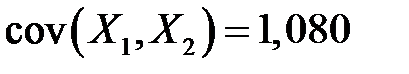 ,
, 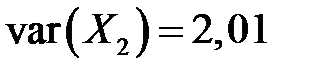 .
.
Тогда ковариационная матрица примет вид
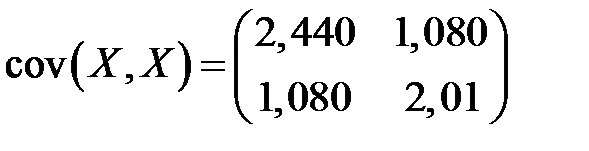 ,
, 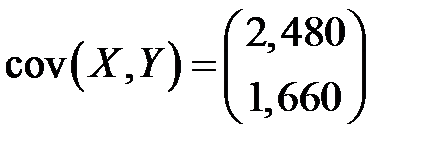 .
.
Обратная матрица
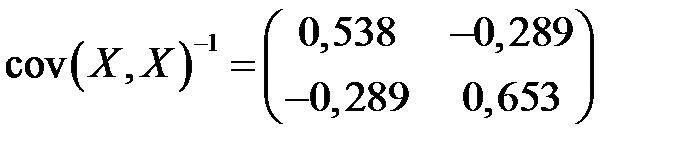 .
.
В таком случае, обнаруживаем
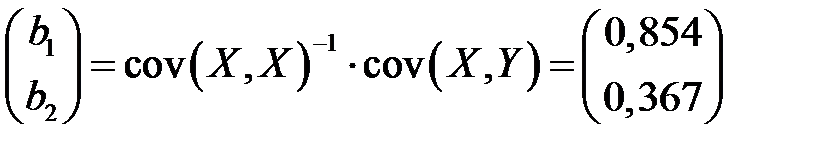 .
.
Отсюда уже находим коэффициент
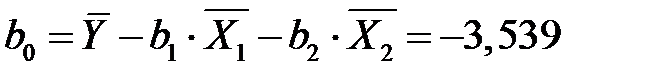 .
.
Значит, уравнение регрессии 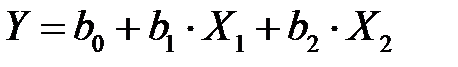 принимает вид
принимает вид
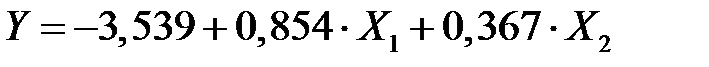 .
.
Дата добавления: 2018-09-24; просмотров: 618;
