Предпосылки множественного регрессионного анализа
Рассмотрим модель множественной линейной регрессии
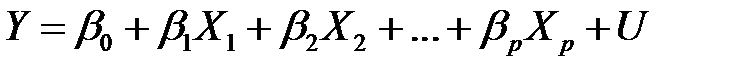 . (МЛР_1)
. (МЛР_1)
Результаты наблюдений 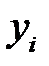 и
и 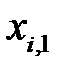 ,
, 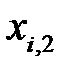 , …,
, …, 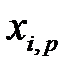 можно рассматривать как значения случайных величин
можно рассматривать как значения случайных величин 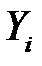 и
и 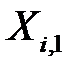 ,
, 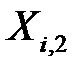 , …,
, …, 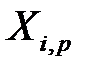 и имеющих такое распределение как случайные величины
и имеющих такое распределение как случайные величины 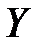 и
и 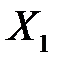 ,
, 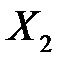 , …,
, …, 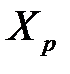 соответственно. В этом случае линейная множественная регрессионная модель (МЛР_1) имеет вид
соответственно. В этом случае линейная множественная регрессионная модель (МЛР_1) имеет вид
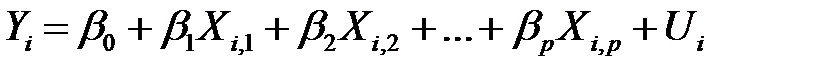 ,
, 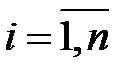 . (МЛР_2)
. (МЛР_2)
Последнюю можно записать в векторной форме
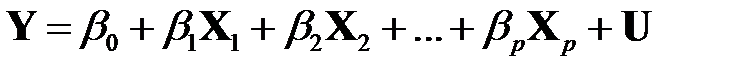 , (МЛР_3)
, (МЛР_3)
где 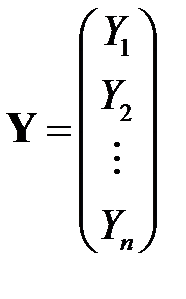 – вектор значений зависимой переменной размерности
– вектор значений зависимой переменной размерности 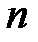 ,
, 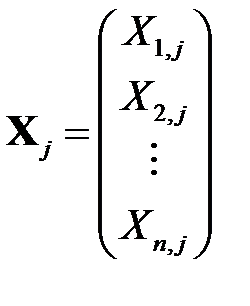 ,
, 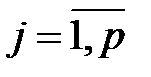 , – векторы значений объясняющих переменных размерности
, – векторы значений объясняющих переменных размерности 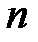 ,
, 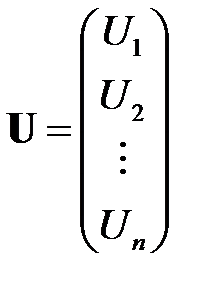 – вектор возмущений (случайных ошибок, остатков) размерности
– вектор возмущений (случайных ошибок, остатков) размерности 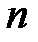 , или в матричной форме
, или в матричной форме
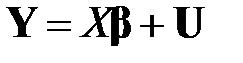 , (МЛР_4)
, (МЛР_4)
где
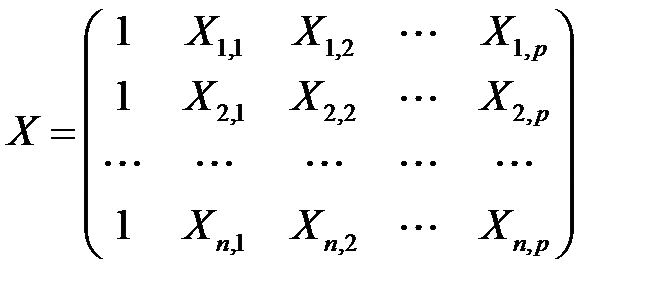 (МЛР_5)
(МЛР_5)
матрица значений объясняющих переменных, или матрицы плана, размерности 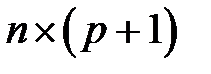 ;
;
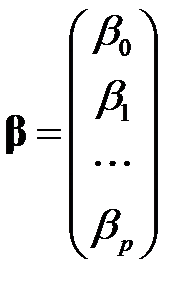 (МЛР_6)
(МЛР_6)
вектор параметров размерности 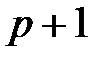 .
.
Модель (МЛР_4) удовлетворяет предпосылкам множественного регрессионного анализа, если выполняются следующие условия.
(РА1) В модели (МЛР_4) вектор возмущения 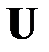 , (или вектор значений
, (или вектор значений 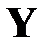 ) есть случайный вектор, а матрица значений
) есть случайный вектор, а матрица значений 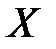 объясняющих переменных
объясняющих переменных 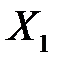 ,
, 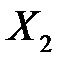 , …,
, …, 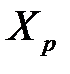 – не случайная (детерминированная) матрица.
– не случайная (детерминированная) матрица.
(РА2) Математическое ожидание вектора возмущения 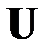 является нулевым вектором
является нулевым вектором
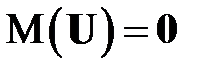 (МЛР_7)
(МЛР_7)
или математическое ожидание зависимого вектора 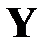 равно линейной функции регрессии
равно линейной функции регрессии
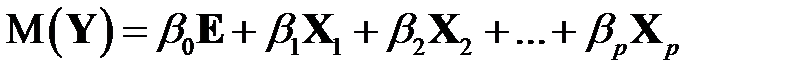 .
.
(РА3), (РА4) Вектор возмущений 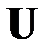 удовлетворяет условиям
удовлетворяет условиям
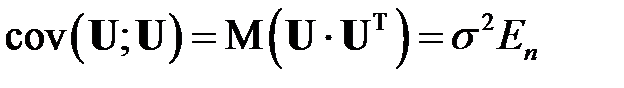 . (МЛР_8)
. (МЛР_8)
(РА5). Возмущение  (или зависимая переменная
(или зависимая переменная 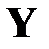 ) являются нормально распределенными случайными векторами, то есть
) являются нормально распределенными случайными векторами, то есть 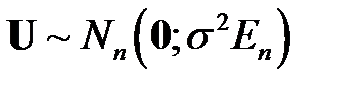 .
.
(РА6) Векторы значений объясняющих переменных  ,
, 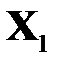 ,
,  , …,
, …, 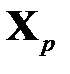 или столбцы матрицы значений
или столбцы матрицы значений  объясняющих переменных (или матрицы плана), размерности
объясняющих переменных (или матрицы плана), размерности 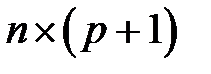 , должны быть линейно независимыми, то есть ранг матрицы
, должны быть линейно независимыми, то есть ранг матрицы 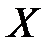 – максимальный
– максимальный 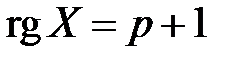 .
.
Кроме того, предполагается, что число имеющихся наблюдений (значений) каждой из объясняющих и зависимой переменных превосходит ранг матрицы 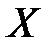 , то есть
, то есть 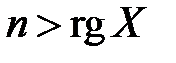 .
.
Модель (МЛР_4) удовлетворяющая предпосылкам (РА1) – (РА6) называется классической нормальной линейной моделью множественной регрессии (Classical Normal Linear Multiple Regression model). Если же среди приведенных не выполняется предпосылка (РА5) о нормальном законе вектора возмущений 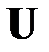 , то модель (МЛР_4) называется просто классической линейной моделью множественной регрессии.
, то модель (МЛР_4) называется просто классической линейной моделью множественной регрессии.
Для получения уравнения регрессии достаточно предпосылок (РА1) – (РА4), (РА6). Требование выполнения предпосылки (5) необходимо для оценки точности уравнения регрессии и его параметров.
Умножим равенство (МЛР_4) слева на матрицу 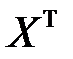
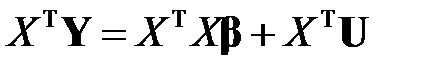 .
.
Вектор оценок 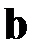 вектора параметров
вектора параметров 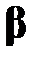 модели (МЛР_4) определяется из равенства (М13), то есть
модели (МЛР_4) определяется из равенства (М13), то есть 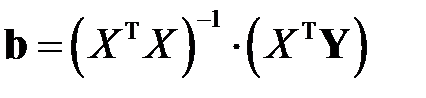 . В таком случае, выражение для вектора оценок примет вид
. В таком случае, выражение для вектора оценок примет вид
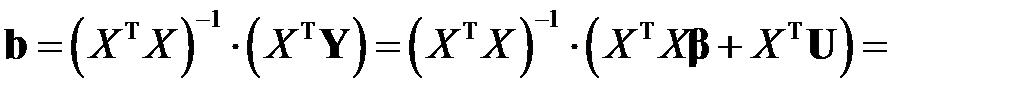
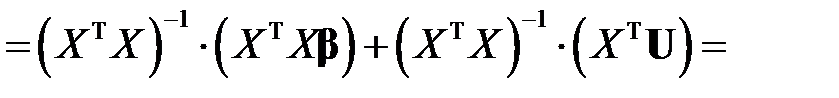
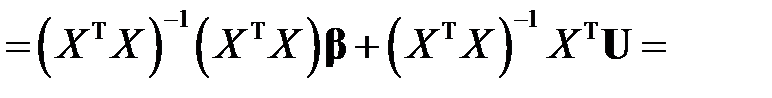
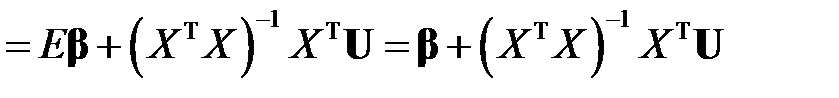 ,
,
то есть
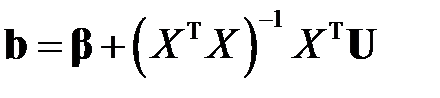 .
.
Таким образом, оценки параметров (М13), найденные по выборке, будут содержать случайные ошибки.
Кроме того, из этого равенства получаем
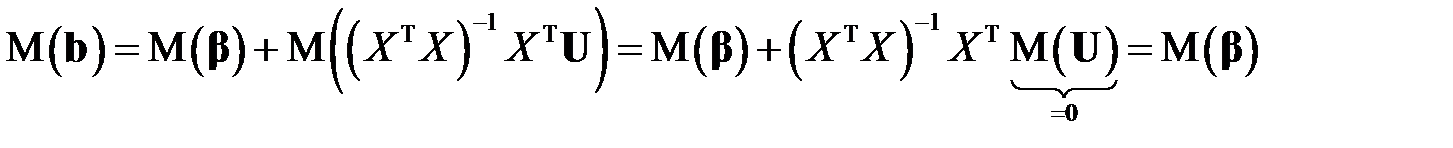
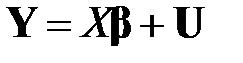
Дата добавления: 2018-09-24; просмотров: 1059;
