Нелинейные модели регрессии
До сих пор мы рассматривали линейные регрессионные модели, в которых переменные имели первую степень (модели, линейные по переменным), а параметры выступали в виде коэффициентов при этих переменных (модели, линейные по параметрам). Однако соотношение между социально-экономическими явлениями и процессами далеко не всегда можно выразить линейными функциями, так при этом могут возникнуть неоправданно большие ошибки.
Так, например, не линейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом, капиталом и т. п.), функции спроса (зависимости между спросом на товары или услуги и их ценами или доходом) и другие.
Для оценки параметров нелинейных моделей используют два подхода.
Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными.
Второй подход обычно применяется в случае, когда подобрать соответствующее линеаризующее преобразование не удается. В этом случае применяются методы нелинейной оптимизации на основе исходных переменных.
Для линеаризации модели в рамках первого подхода могут использоваться как модели, не линейные по переменным, так и не линейные по параметрам.
Если модель нелинейная по переменным, то введением новых переменных ее можно свести к линейной модели, для оценки параметров которой использовать обычный метод наименьших квадратов.
Например, для оценки параметров регрессионной модели
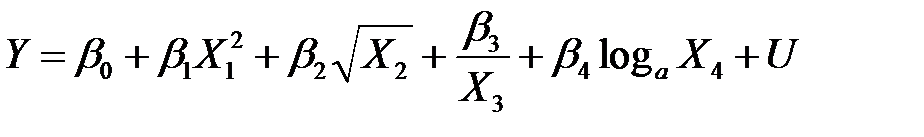 ,
,
введением новых переменных
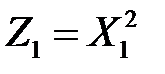 ,
, 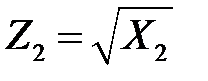 ,
, 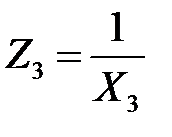 и
и 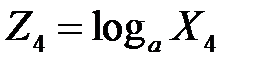 ,
,
приведем данную регрессионную модель к линейной модели
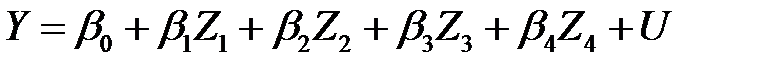 ,
,
параметры которой совпадают с параметрами исходной модели.
Обратим внимание на недостаток такой замены переменных, связанный с тем, что вектор оценок 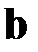 получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. В связи с этим необходимо некоторое уточнение полученных оценок.
получается не из условия минимизации суммы квадратов отклонений для исходных переменных, а из условия минимизации суммы квадратов отклонений для преобразованных переменных, что не одно и то же. В связи с этим необходимо некоторое уточнение полученных оценок.
Более сложной проблемой является нелинейность модели по параметрам, так как непосредственное применение метода наименьших квадратов для их оценивания невозможно. К числу таких моделей относят, например, мультипликативную (степенную) модель
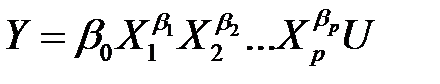 , (НЛР_1)
, (НЛР_1)
экспоненциальную модель
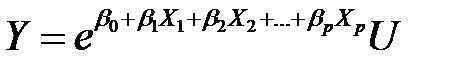 , (НЛР_2)
, (НЛР_2)
а так же другие модели.
В ряде случаев, путем подходящих преобразований эти модели удается привести к линейной форме. Логарифмированием, модели (НЛР_1) и (НЛР_2) приводятся к линейным. Именно,
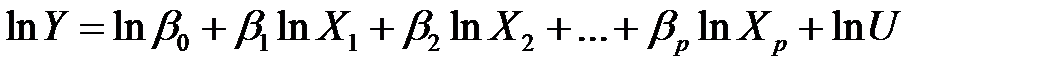 . (НЛР_3)
. (НЛР_3)
К модели (НЛР_3) уже можно применять обычные методы исследования линейной регрессии. Однако следует подчеркнуть, что критерии значимости и интервальные оценки параметров, применяемые для нормальной линейной регрессии, требуют, чтобы нормальный закон распределения в моделях (НЛР_1) и (НЛР_2) имел логарифм вектора возмущений 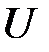 , то есть
, то есть 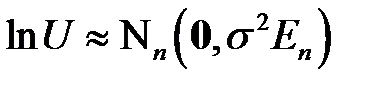 , а вовсе не
, а вовсе не 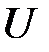 . Другими словами, вектор возмущений
. Другими словами, вектор возмущений 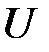 должен иметь логарифмически нормальное распределение.
должен иметь логарифмически нормальное распределение.
Попутно отметим, что к модели
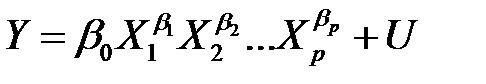 , (НЛР_4)
, (НЛР_4)
рассматриваемой в качестве альтернативной по отношению к модели (НЛР_1), изложенные выше методы исследования линейной регрессии уже непригодны, так как модель (НЛР_4) нельзя привести к линейному виду. В этом случае используют специальные (итеративные) процедуры оценивания параметров.
Для наиболее часто встречающихся зависимостей парной регрессионной модели, эмпирическую формулу можно выбирать с помощью таблицы 4.1.
Для проверки пригодности выбранной эмпирической формулы, используя исходные данные, находят 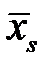 и
и 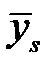 по формулам, приведенным в таблице 4.1. Если
по формулам, приведенным в таблице 4.1. Если 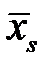 находится среди исходных данных
находится среди исходных данных 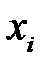 ,
, 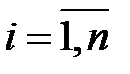 , то в качестве
, то в качестве 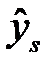 возьмем
возьмем 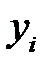 . Если
. Если 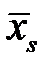 не находится среди исходных данных
не находится среди исходных данных 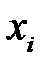 ,
, 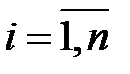 , то найдем такой индекс
, то найдем такой индекс 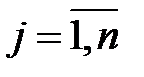 , что
, что 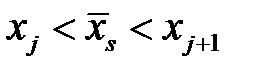 и определим
и определим 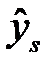 с помощью линейной интерполяции
с помощью линейной интерполяции
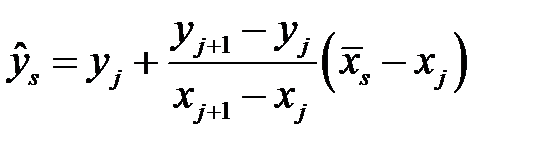 . (НЛР_5)
. (НЛР_5)
Далее среди величин 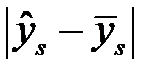 находим самую маленькую. Ей соответствует выбираемая эмпирическая формула.
находим самую маленькую. Ей соответствует выбираемая эмпирическая формула.
Таблица 4.1.
| Номер формулы | 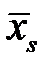
| 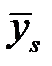
| Вид эмпирической формулы |
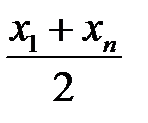
| 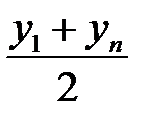
| 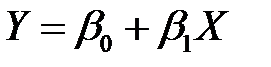
| |
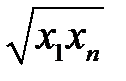
| 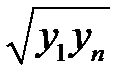
| 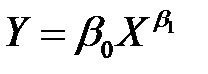
| |
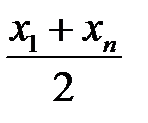
| 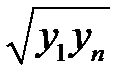
| 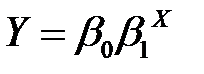
| |
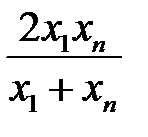
| 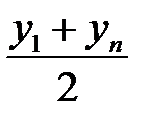
| 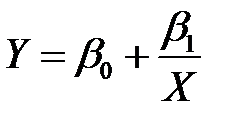
| |
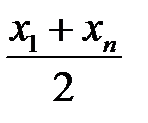
| 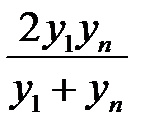
| 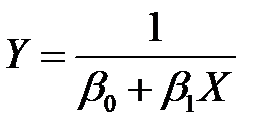
| |
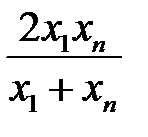
| 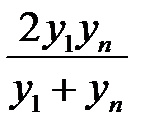
| 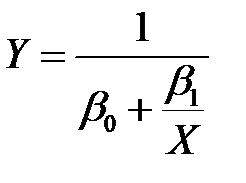
| |
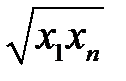
| 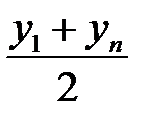
| 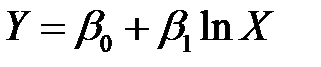
|
Пример. Имеются данные о цене на нефть и соответствующим индексом нефтяных компаний
| Цена на нефть, X | Индекс нефтяных компаний, Y |
| 0,07 | 29,033 |
| 0,14 | 15,074 |
| 0,21 | 10,028 |
| 0,28 | 8,780 |
| 0,35 | 10,316 |
| 0,42 | 6,544 |
| 0,49 | 4,984 |
| 0,56 | 7,085 |
| 0,63 | 8,046 |
| 0,7 | 4,152 |
| 0,77 | 5,982 |
| 0,84 | 4,190 |
| 0,91 | 4,689 |
| 0,98 | 4,061 |
| 1,05 | 3,482 |
Определить вид эмпирической формулы и построить соответствующую нелинейную модель.
Решение. Определяем вид эмпирической формулы. Для этого строим таблицу 4.2.
Таким образом, эмпирическая формула регрессии
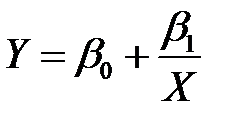 .
.
Таблица 4.2.
| номер формулы | 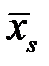
| 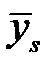
| 
| 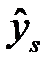
| 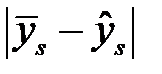
|
| 0,560 | 16,257 | 7,085 | 9,172 | ||
| 0,271 | 10,054 | 8,939 | 1,116 | ||
| 0,560 | 10,054 | 7,085 | 2,969 | ||
| 0,131 | 16,257 | 16,819 | 0,561 | ||
| 0,560 | 6,218 | 7,085 | 0,867 | ||
| 0,131 | 6,218 | 16,819 | 10,601 | ||
| 0,271 | 16,257 | 8,939 | 7,319 |
Введением переменной 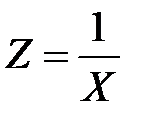 приводим нелинейную модель к линейной
приводим нелинейную модель к линейной
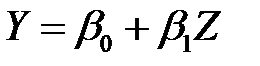 .
.
Находим параметры данной линейной модели. Для этого строим таблицу 4.3.
Таблица 4.3.
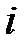
| 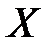
| 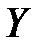
| 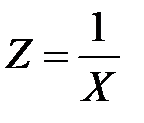
| 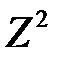
| 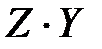
| 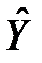
|
| 0,07 | 29,033 | 14,28571 | 204,0816 | 414,756 | 28,647 | |
| 0,14 | 15,074 | 7,142857 | 51,02041 | 107,6706 | 15,667 | |
| 0,21 | 10,028 | 4,761905 | 22,67574 | 47,75467 | 11,340 | |
| 0,28 | 8,780 | 3,571429 | 12,7551 | 31,35695 | 9,177 | |
| 0,35 | 10,316 | 2,857143 | 8,163265 | 29,47307 | 7,879 | |
| 0,42 | 6,544 | 2,380952 | 5,668934 | 15,5816 | 7,014 | |
| 0,49 | 4,984 | 2,040816 | 4,164931 | 10,17057 | 6,396 | |
| 0,56 | 7,085 | 1,785714 | 3,188776 | 12,65196 | 5,932 | |
| 0,63 | 8,046 | 1,587302 | 2,519526 | 12,77135 | 5,571 | |
| 0,7 | 4,152 | 1,428571 | 2,040816 | 5,931865 | 5,283 | |
| 0,77 | 5,982 | 1,298701 | 1,686625 | 7,768647 | 5,047 | |
| 0,84 | 4,190 | 1,190476 | 1,417234 | 4,987778 | 4,850 | |
| 0,91 | 4,689 | 1,098901 | 1,207584 | 5,152706 | 4,684 | |
| 0,98 | 4,061 | 1,020408 | 1,041233 | 4,143729 | 4,541 | |
| 1,05 | 3,482 | 0,952381 | 0,907029 | 3,31617 | 4,418 | |
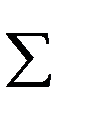
| 8,4 | 126,445 | 47,40327 | 322,5388 | 713,4876 | 126,445 |
| среднее | 0,56 | 8,430 | 3,160218 | 21,50259 | 47,56584 | 8,430 |
Определяем
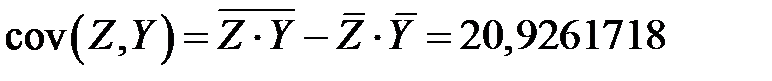 ,
,
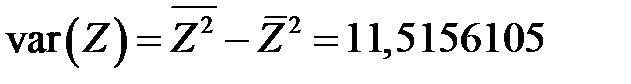 .
.
Тогда
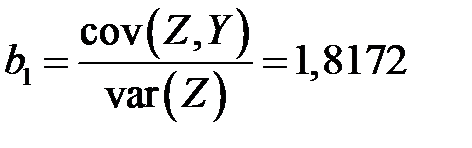 ,
,
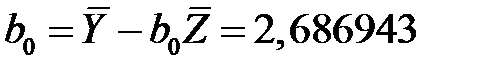 .
.
Получаем регрессионную модель
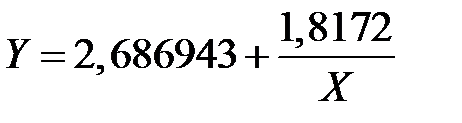
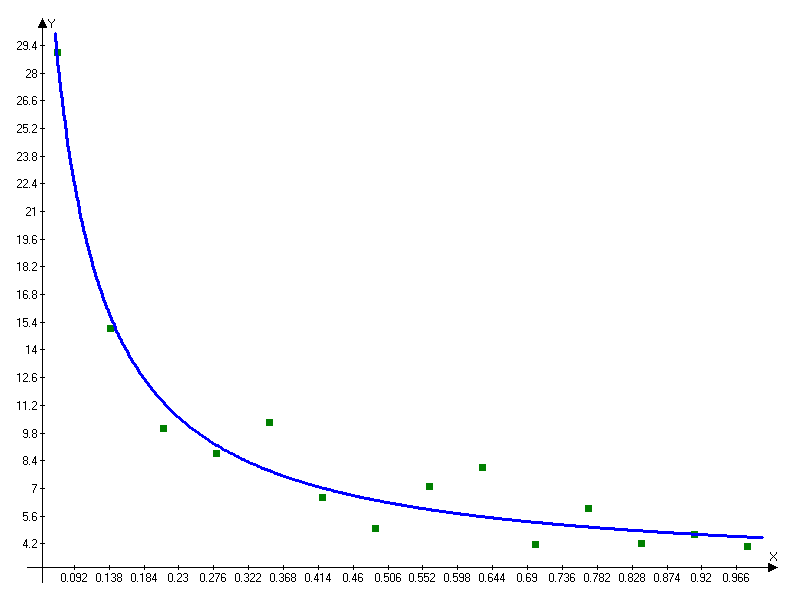
Раздел 2.
Дата добавления: 2018-09-24; просмотров: 1045;
