Отбор наиболее существенных объясняющих переменных регрессионной модели
Литература
Основная литература
1. Андерсон Д. А. Дискретная математика и комбинаторика. / Д. А. Андерсон – пер. с англ. – Москва: Издательский дом «Вильямс», 2004. − 960 с.
2. Бурбаки Н. Теория множеств. / Н. Бурбаки – пер. с фр. – Москва: Издательский дом «Либроком», 2010. − 456 с.
3. Воеводин В. В. Линейная алгебра. Учеб. пособие / В. В. Воеводин – СПб.: «Лань», 2009. – 416 с.
4. Зубрилин К. М. Линейная алгебра: учебное пособие. / К. М. Зубрилин – Керчь: Изд-во ФГБОУ ВО «КГМТУ», 2017. – 371 с. Илл.: 95.
5. Зубрилин К. М. Линейная алгебра: практикум. / К. М. Зубрилин – Керчь: Изд-во ФГБОУ ВО «КГМТУ», 2017. – 252 с. Илл.: 80.
6. Курош А. Г. Курс высшей алгебры. Учебник. / А. Г. Курош – СПб.: «Лань» 2011. – 432 с.
7. Постников М. М. Аналитическая геометрия. Учебное пособие. / М. М. Постников – 3-е изд., испр. – СПб.: «Лань» 2009. – 416 с.
8. Постников М. М. Линейная алгебра. Учебное пособие. / М. М. Постников – 3-е изд., испр. – СПб.: «Лань» 2009. – 400 с.
9. Проскуряков И. В. Сборник задач по линейной алгебре / И. В. Проскуряков. – 9-е изд. – Москва: БИНОМ. Лаборатория знаний, 2005. — 383 с: ил.
10. Цубербиллер О. Н. Задачи и упражнения по аналитической геометрии. / О. Н. Цубербиллер – 34-е изд., стер. – СПб.: «Лань» 2009. – 336 с.
Дополнительная литература
11. Апатенок Р. Ф. Сборник задач по линейной алгебре и аналитической геометрии. Учеб. пособие / Р. Ф. Апатенок, А. М. Маркина, В. Б. Хейнман ; под ред. В. Т. Воднева. – Минск: Высшая школа, 1990. – 285 с. : ил.
12. Бурбаки Н. Алгебраические структуры. Линейная и полилинейная алгебра. / Н. Бурбаки – OZON.ru 2012. – 516 с.
13. Гантмахер Ф. Р. Теория матриц. / Ф. Р. Гантмахер – 5-е изд. – Москва: ФИЗМАТЛИТ, 2010. – 560 с.
14. Моденов П.С. Аналитическая геометрия. Учебник. / П. С. Моденов. – Москва: МГУ, 1969. – 699 с.
[1] математического ожидания случайной величины 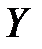 , вычисленного в предположении, что случайная величина
, вычисленного в предположении, что случайная величина 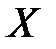 приняла значение
приняла значение 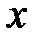
Дата добавления: 2018-09-24; просмотров: 709;
