Оценка значимости уравнения регрессии
Доверительный интервал для параметра 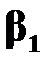 . Можно показать, что при выполнении предпосылки (5) регрессионного анализа статистика
. Можно показать, что при выполнении предпосылки (5) регрессионного анализа статистика 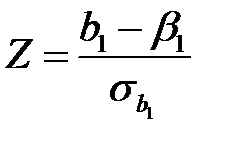 имеет стандартный нормальный закон распределения. Согласно предпосылки (5) регрессионного анализа, случайная величина
имеет стандартный нормальный закон распределения. Согласно предпосылки (5) регрессионного анализа, случайная величина 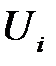 имеет нормальный закон распределения. Учитывая предпосылки (2) и (3), случайная величина
имеет нормальный закон распределения. Учитывая предпосылки (2) и (3), случайная величина 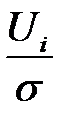 имеет стандартный нормальный закон распределения. Тогда случайная величина
имеет стандартный нормальный закон распределения. Тогда случайная величина 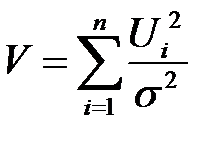 имеет распределение
имеет распределение 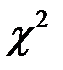 с
с 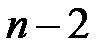 степенями свободы. Тогда случайная величина
степенями свободы. Тогда случайная величина
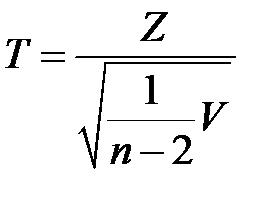
имеет распределение Стьюдента с 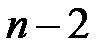 степенями свободы. Очевидно
степенями свободы. Очевидно
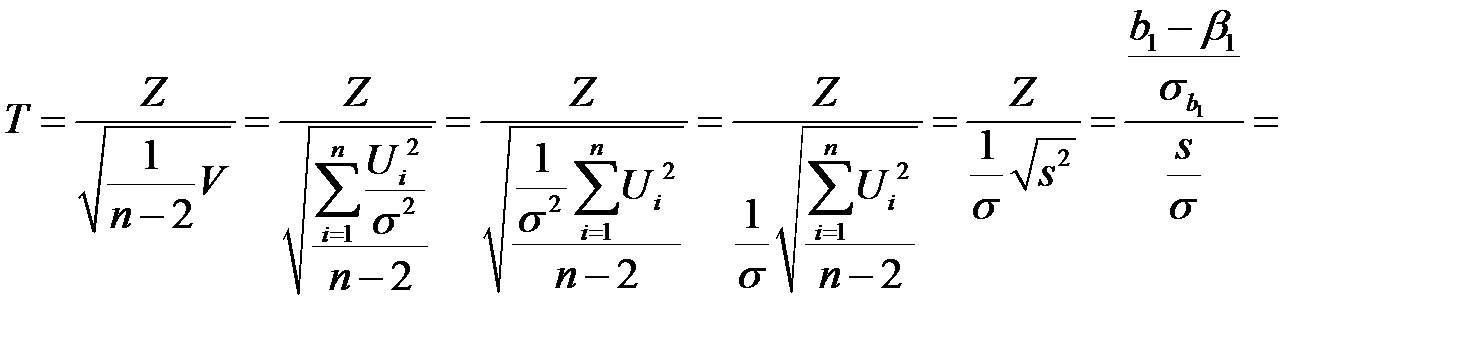
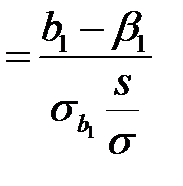 .
.
Для нахождения дисперсии 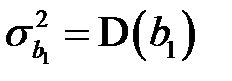 представим коэффициент
представим коэффициент 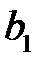 в виде
в виде
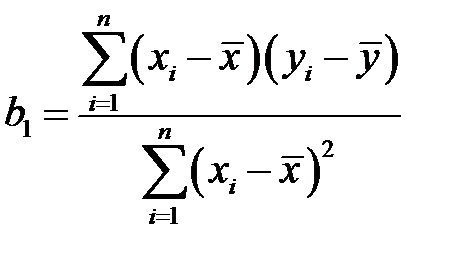 ,
,
подставив правые части равенств (К10) и (К11) в первое равенство (К9). Поскольку 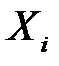 не случайная величина, а
не случайная величина, а 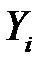 – случайная величина, то
– случайная величина, то
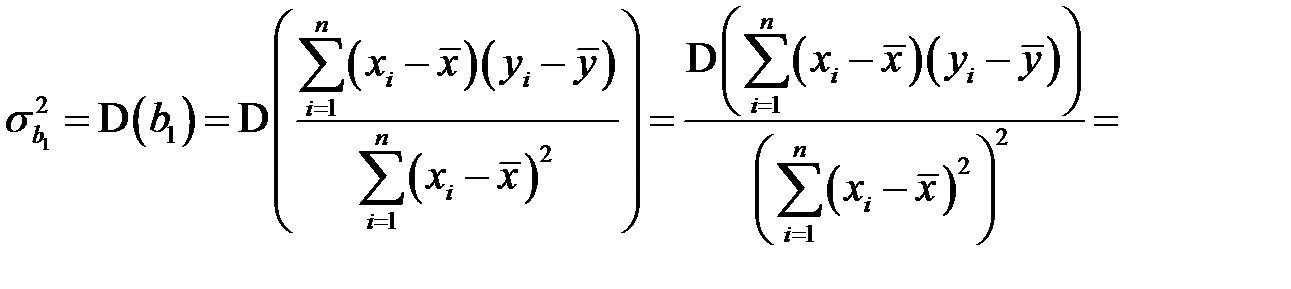
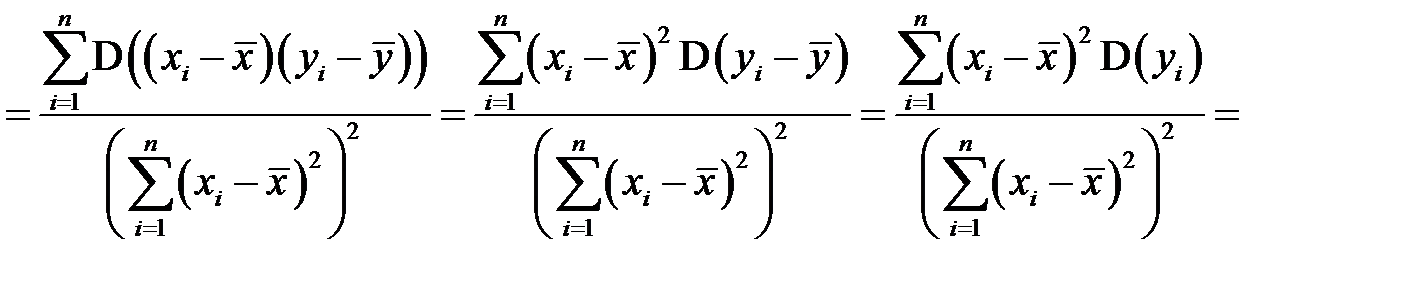
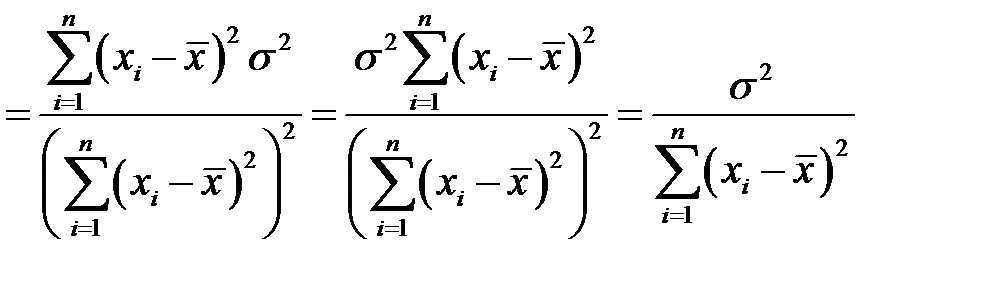 ,
,
то есть
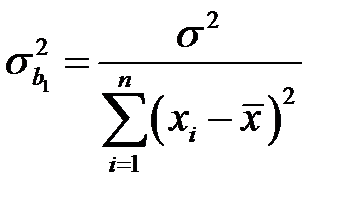 и
и 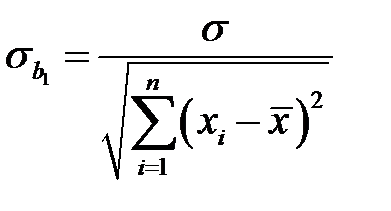 . (К19)
. (К19)
В таком случае, получаем случайную величину
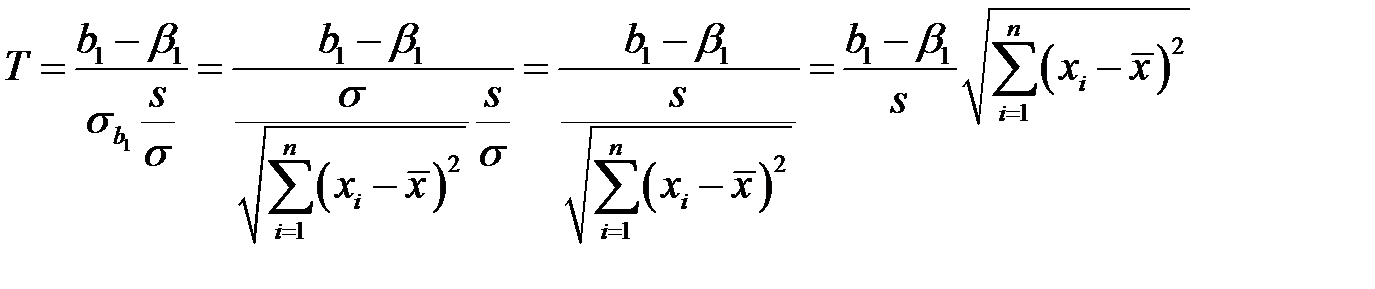
имеющую распределение Стьюдента с 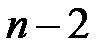 степенями свободы.
степенями свободы.
Для уровня значимости 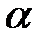 по таблице критических точек распределения Стьюдента находим критическое значение
по таблице критических точек распределения Стьюдента находим критическое значение 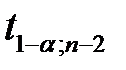 . Доверительный интервал определяем из неравенства
. Доверительный интервал определяем из неравенства 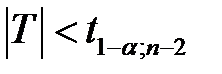 . Получаем
. Получаем
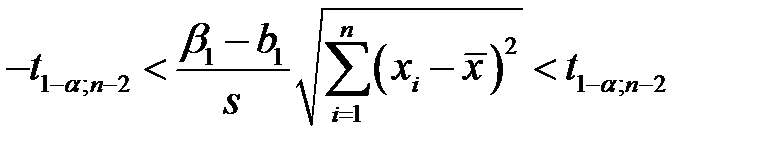 ,
,
умножаем на 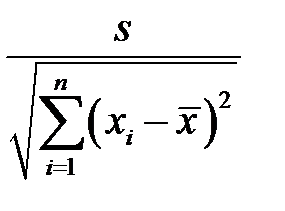 ; получим
; получим
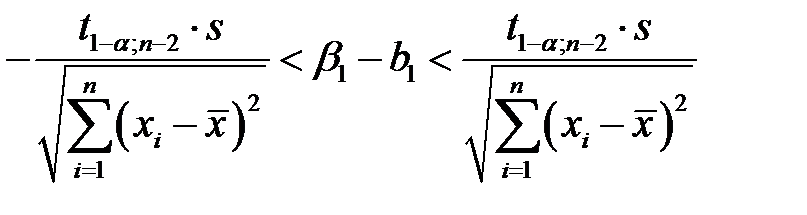 ,
,
прибавляя 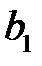 , приходим к искомому доверительному интервалу
, приходим к искомому доверительному интервалу
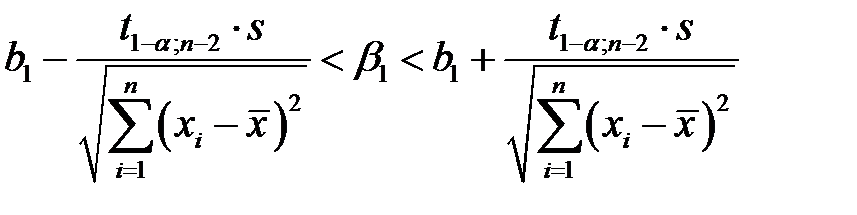 . (К20)
. (К20)
Доверительный интервал для параметра 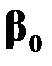 . Подобным образом показываем, что статистика
. Подобным образом показываем, что статистика 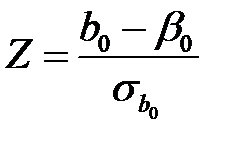 имеет стандартный нормальный закон распределения, а случайная величина
имеет стандартный нормальный закон распределения, а случайная величина 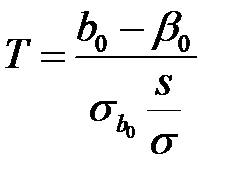 имеет распределение Стьюдента с
имеет распределение Стьюдента с 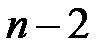 степенями свободы.
степенями свободы.
Для нахождения дисперсии 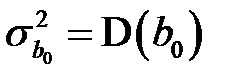 воспользуемся выражением для
воспользуемся выражением для 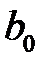 из второго равенства (К9). Будем иметь
из второго равенства (К9). Будем иметь
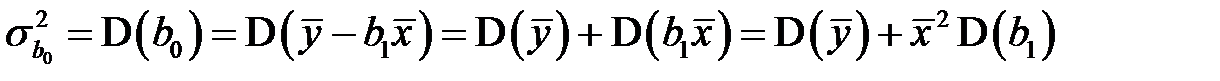 . (К21)
. (К21)
Поскольку 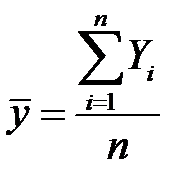 , то по свойству дисперсии
, то по свойству дисперсии
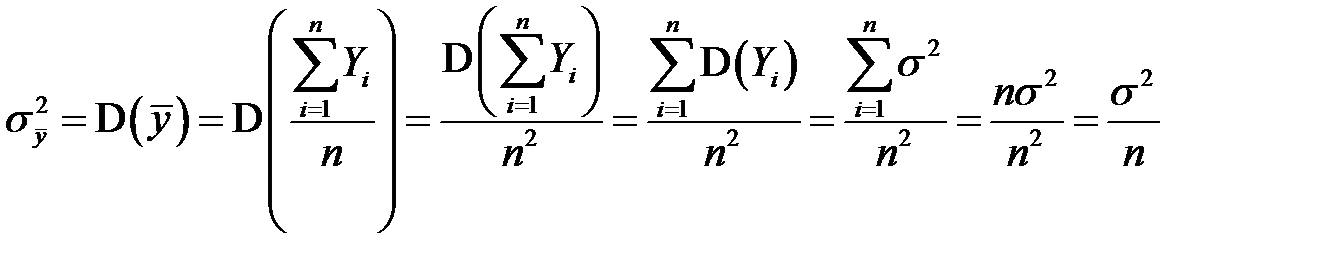 . (К22)
. (К22)
Подставляя правые части равенств (К19) и (К22) в равенство (К21), получим
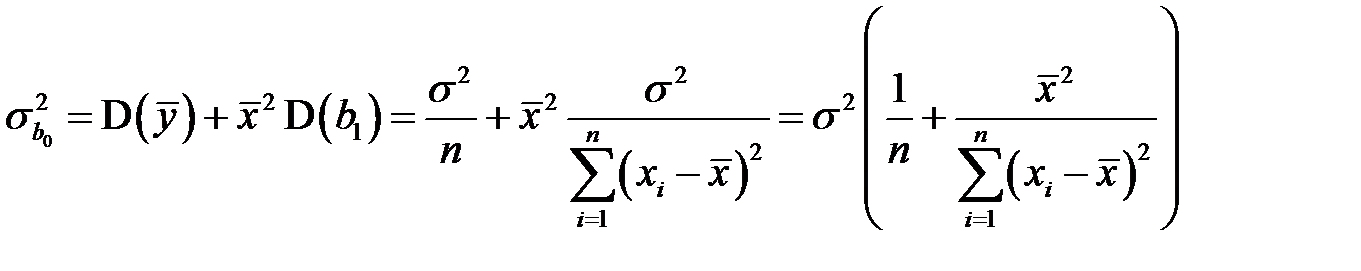 . (К23)
. (К23)
Поскольку
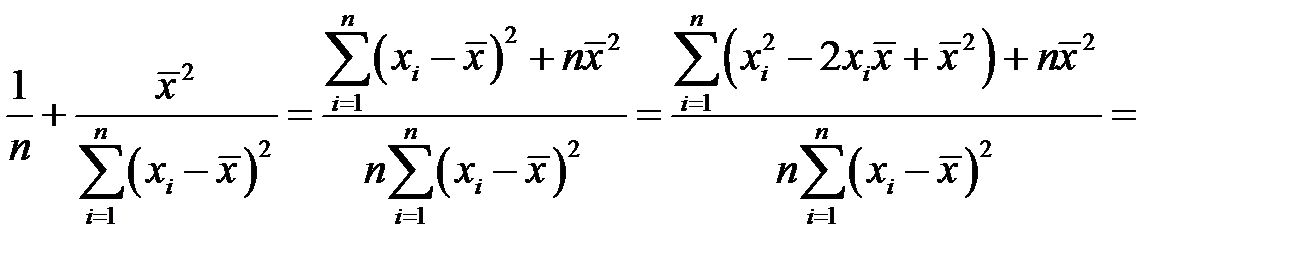
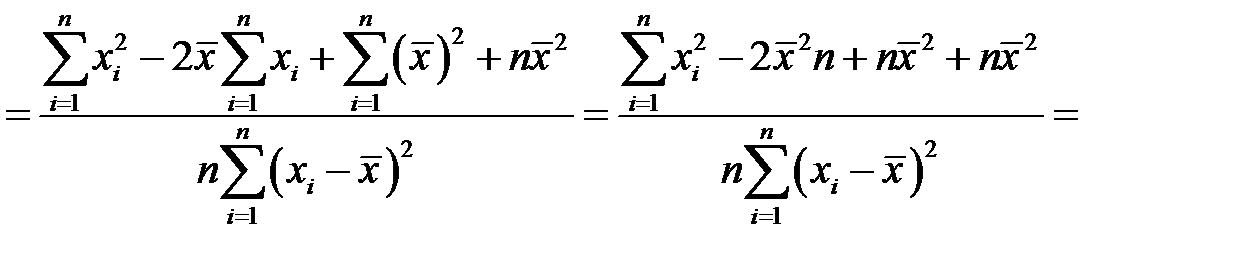
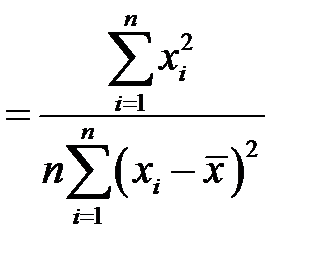 .
.
Учитывая последнее в равенстве (К23), находим
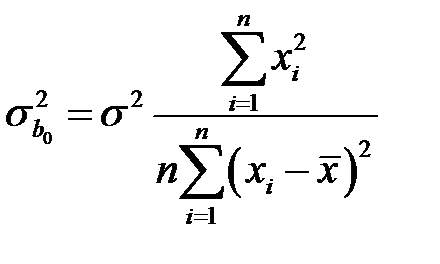 и
и 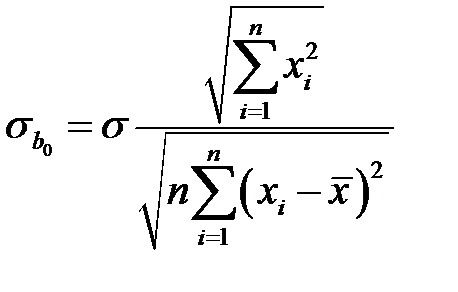 . (К24)
. (К24)
Значит, случайная величина
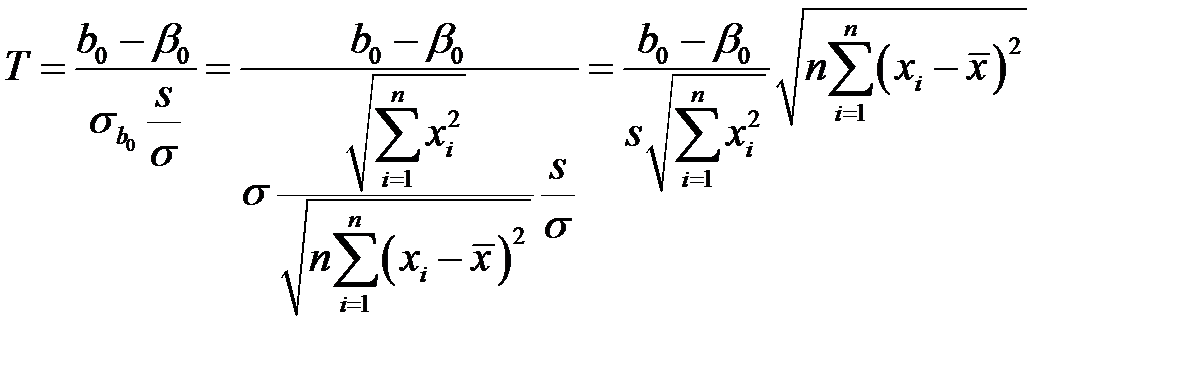 .
.
имеет распределение Стьюдента с 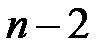 степенями свободы.
степенями свободы.
Для уровня значимости 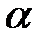 по таблице критических точек распределения Стьюдента находим критическое значение
по таблице критических точек распределения Стьюдента находим критическое значение 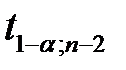 . Доверительный интервал определяем из неравенства
. Доверительный интервал определяем из неравенства 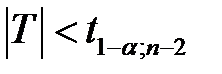 . Получаем
. Получаем
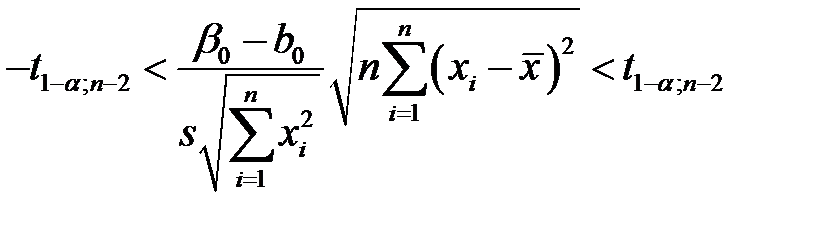 ,
,
умножаем на 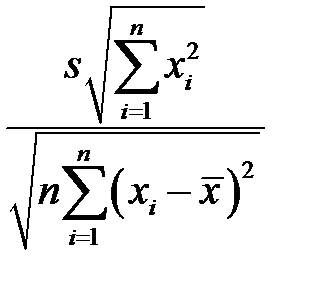 ; получим
; получим
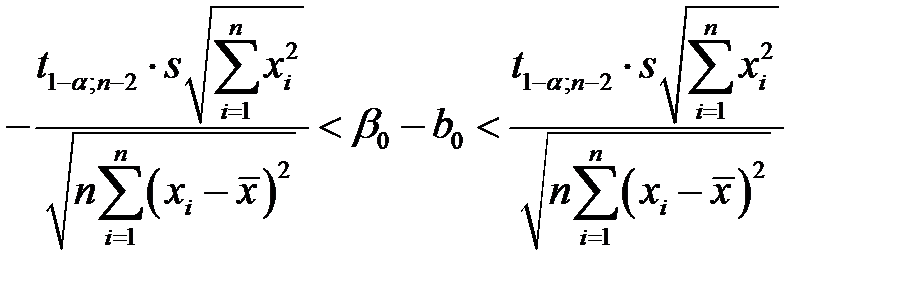 ;
;
прибавляя 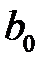 , приходим к искомому доверительному интервалу
, приходим к искомому доверительному интервалу
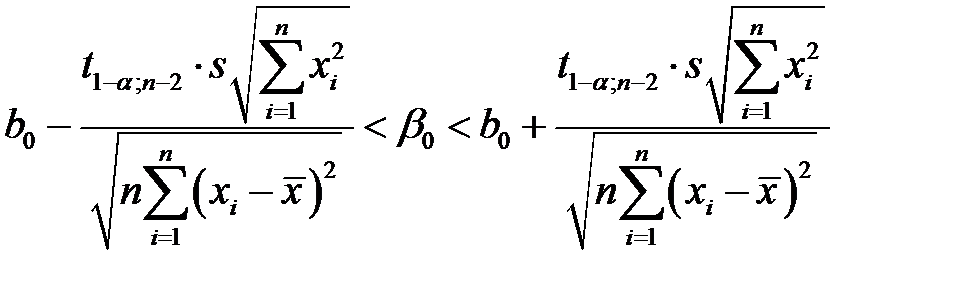 . (К25)
. (К25)
Доверительный интервал для условного математического ожидания 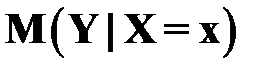 . Построим доверительный интервал для функции регрессии, то есть для условного математического ожидания
. Построим доверительный интервал для функции регрессии, то есть для условного математического ожидания 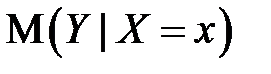 , который с заданной надежностью (доверительной вероятностью)
, который с заданной надежностью (доверительной вероятностью) 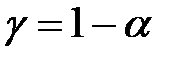 накрывает неизвестное значение
накрывает неизвестное значение 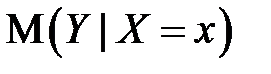 . Случайная величина
. Случайная величина 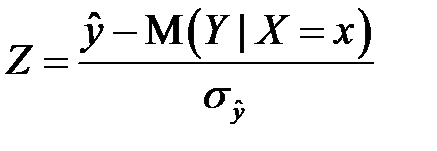 имеет стандартный нормальный закон распределения, а случайная величина
имеет стандартный нормальный закон распределения, а случайная величина 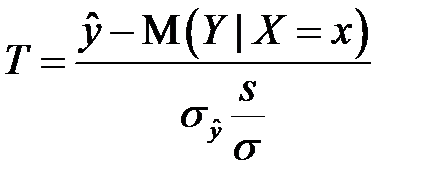 имеет распределение Стьюдента с
имеет распределение Стьюдента с 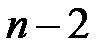 степенями свободы.
степенями свободы.
Для нахождения дисперсии 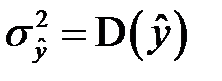 получим выражением для
получим выражением для 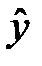 . Для этого правую часть второго равенства (К9) подставим в равенство (К4). Обнаруживаем
. Для этого правую часть второго равенства (К9) подставим в равенство (К4). Обнаруживаем
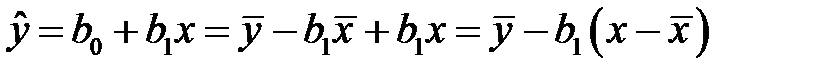 .
.
Теперь, применяя свойства дисперсии, учитывая при этом, что 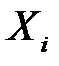 не случайная величина, а
не случайная величина, а 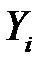 – случайная величина, находим
– случайная величина, находим
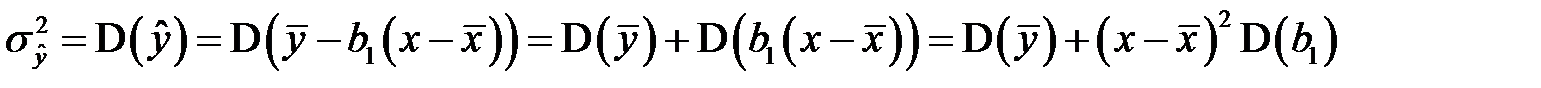 .
.
Подставляя сюда правые части равенств (К19) и (К22), будем иметь
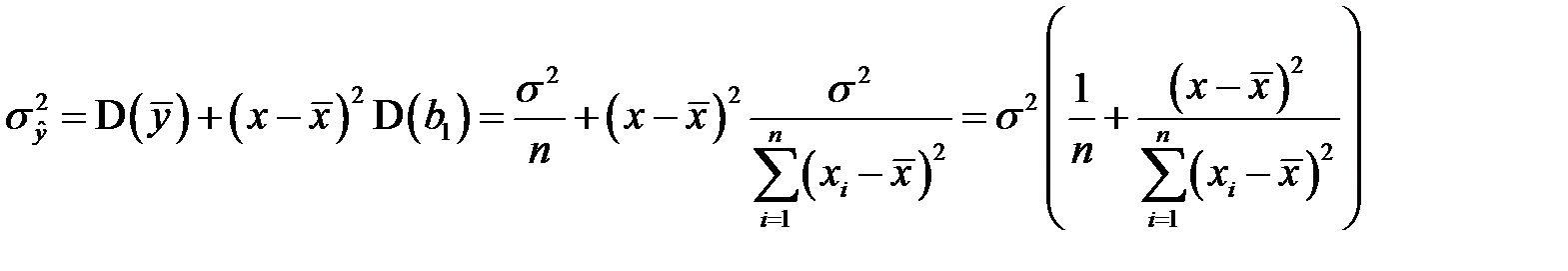 ,
,
то есть
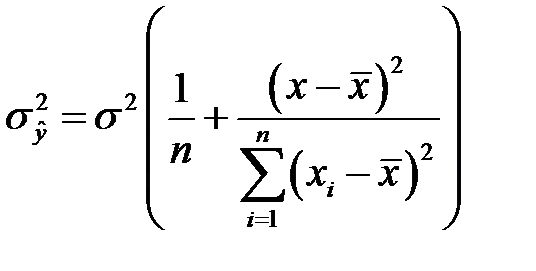 и
и 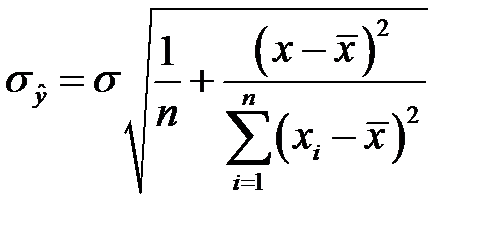 . (К26)
. (К26)
Таким образом, случайная величина
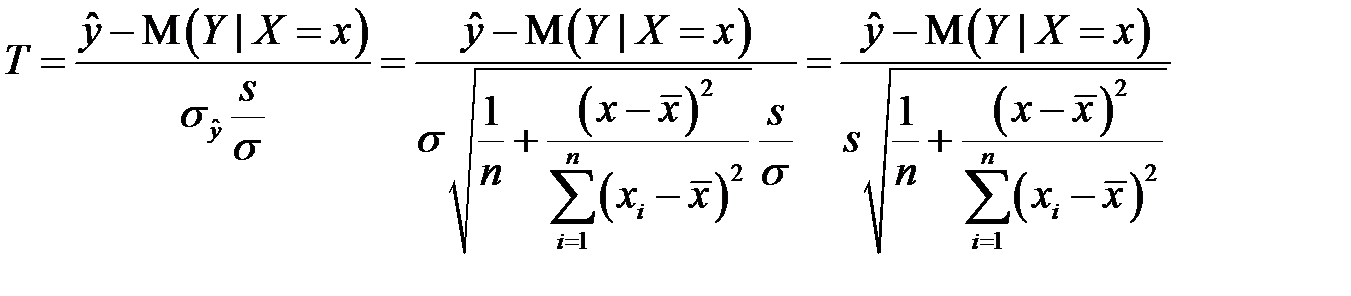
имеет распределение Стьюдента с 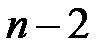 степенями свободы.
степенями свободы.
Для уровня значимости 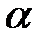 по таблице критических точек распределения Стьюдента находим критическое значение
по таблице критических точек распределения Стьюдента находим критическое значение 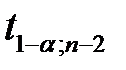 . Доверительный интервал определяем из неравенства
. Доверительный интервал определяем из неравенства 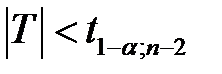 . Получаем
. Получаем
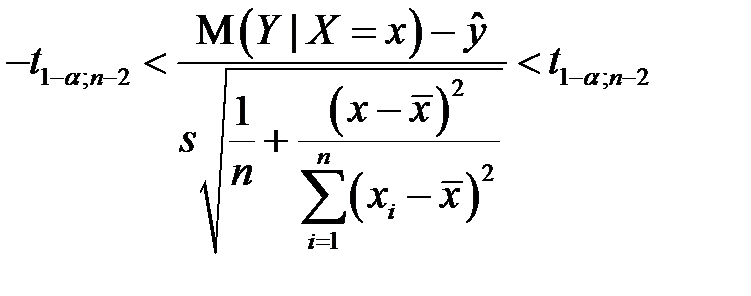 ,
,
умножаем на 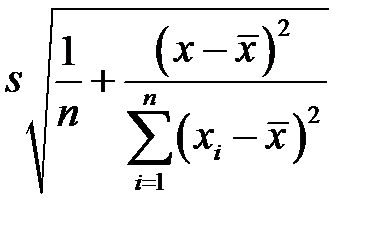 ; получим
; получим
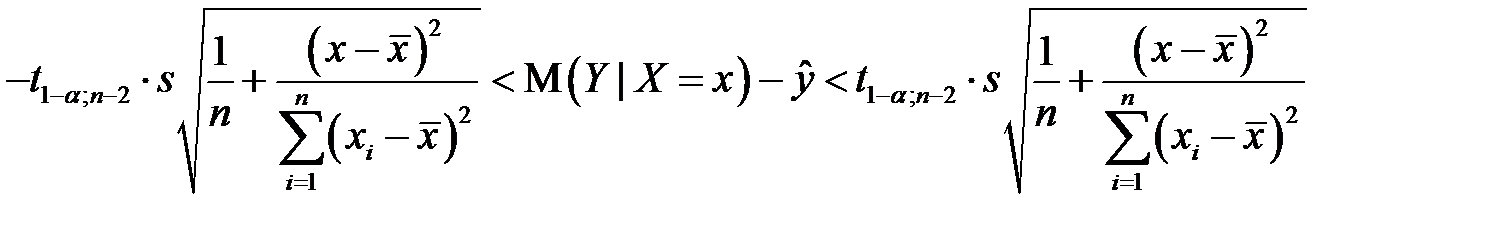 ;
;
прибавляя 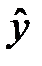 , приходим к искомому доверительному интервалу
, приходим к искомому доверительному интервалу
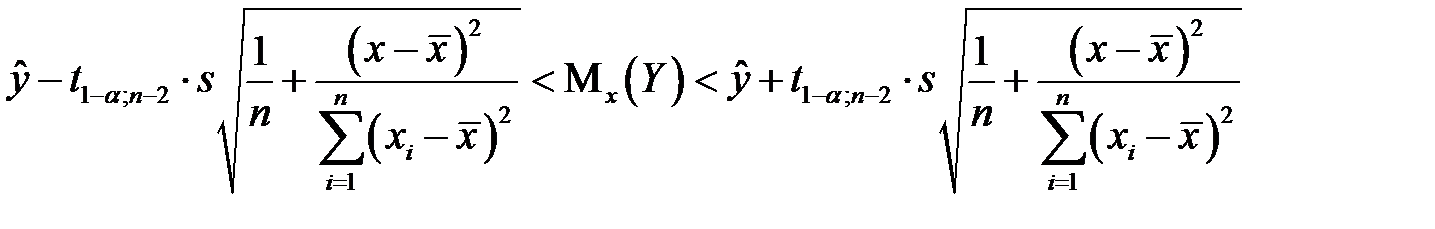 . (К27)
. (К27)
Доверительный интервал для индивидуальных значений зависимой переменной. Построенная доверительная область для 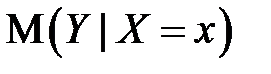 определяет местоположение модельной линии регрессии (то есть условного математического ожидания), но не отдельных возможных значений зависимой переменной, которые отклоняются от средней.
определяет местоположение модельной линии регрессии (то есть условного математического ожидания), но не отдельных возможных значений зависимой переменной, которые отклоняются от средней.
Случайная величина 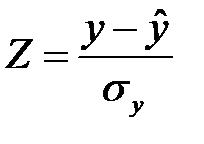 имеет стандартный нормальный закон распределения, а случайная величина
имеет стандартный нормальный закон распределения, а случайная величина 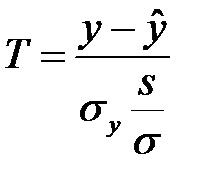 имеет распределение Стьюдента с
имеет распределение Стьюдента с 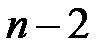 степенями свободы.
степенями свободы.
Для нахождения дисперсии 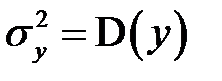 воспользуемся выражением
воспользуемся выражением 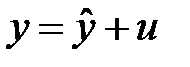 . Имеем, учитывая равенство (К26) и предпосылку (3) регрессионного анализа
. Имеем, учитывая равенство (К26) и предпосылку (3) регрессионного анализа
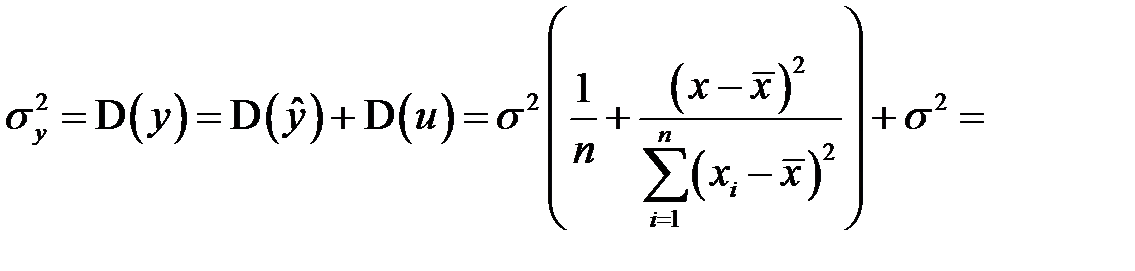
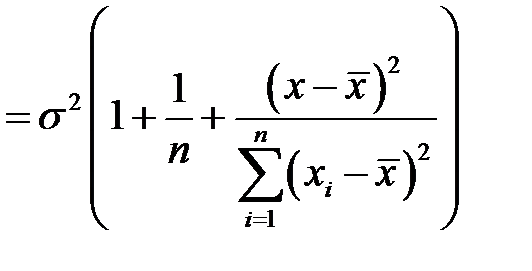 ,
,
то есть
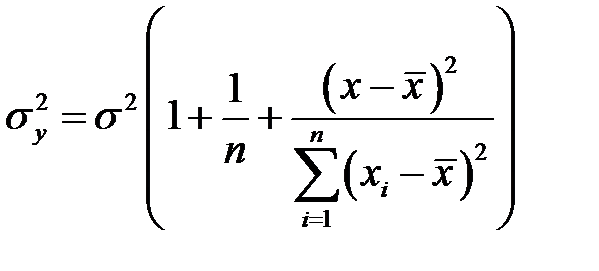 и
и 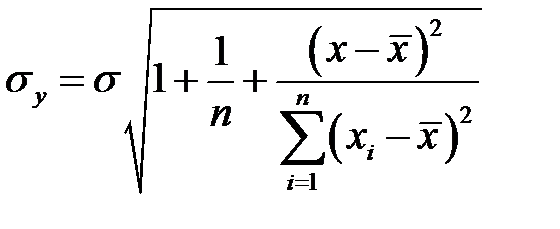 .
.
Таким образом, случайная величина
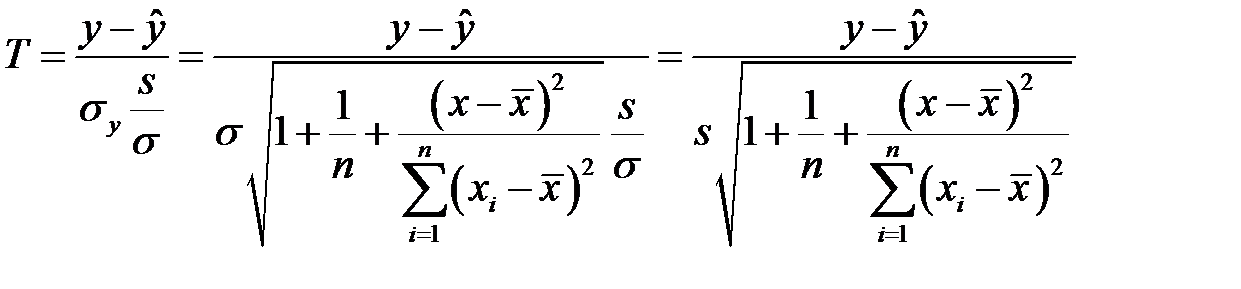
имеет распределение Стьюдента с 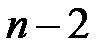 степенями свободы.
степенями свободы.
Для уровня значимости 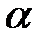 по таблице критических точек распределения Стьюдента находим критическое значение
по таблице критических точек распределения Стьюдента находим критическое значение 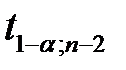 . Доверительный интервал определяем из неравенства
. Доверительный интервал определяем из неравенства 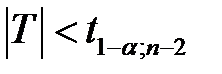 . Получаем
. Получаем
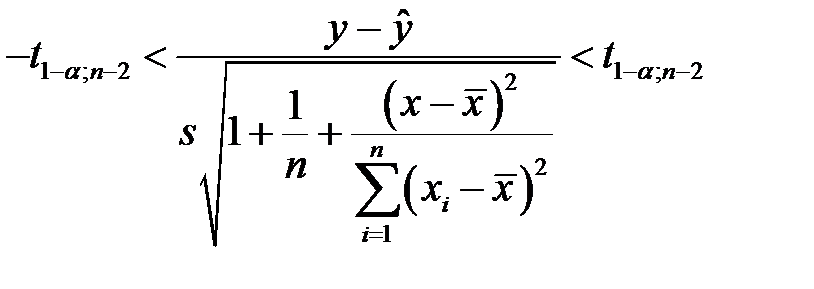 ,
,
умножаем на 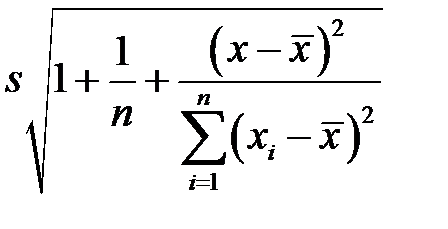 ; получим
; получим
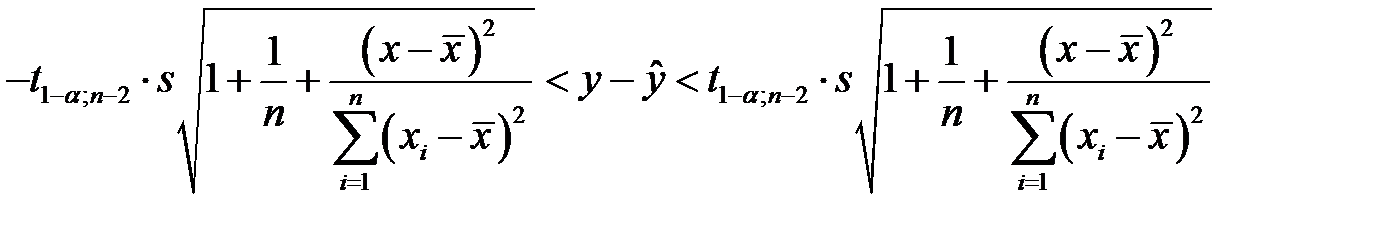
прибавляя 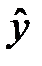 , приходим к искомому доверительному интервалу
, приходим к искомому доверительному интервалу
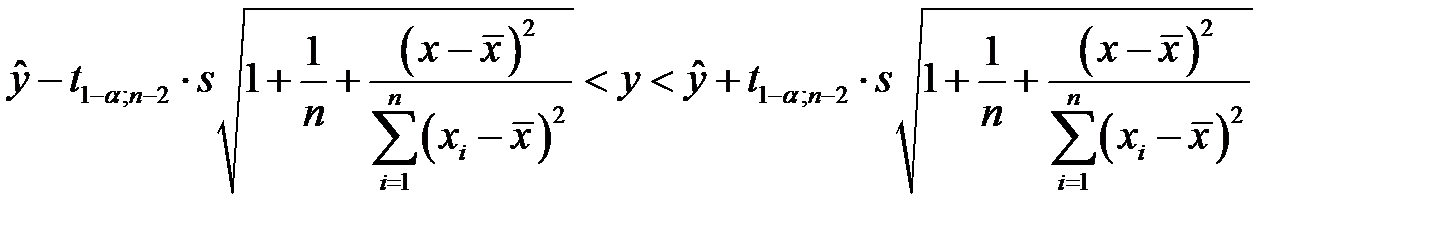 . (К28)
. (К28)
Доверительный интервал для дисперсии 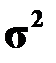 ошибок. Статистика
ошибок. Статистика 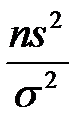 имеет
имеет 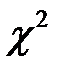 распределение с
распределение с 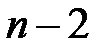 степенями свободы. Доверительный интервал
степенями свободы. Доверительный интервал 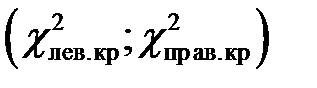 выбирается таким образом, чтобы
выбирается таким образом, чтобы
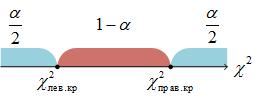
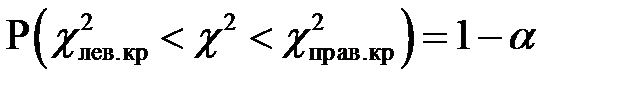 .
.
Однако в таблице критических точек распределения 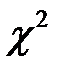 приведены лишь правые границы
приведены лишь правые границы
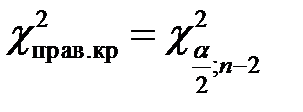 , где
, где 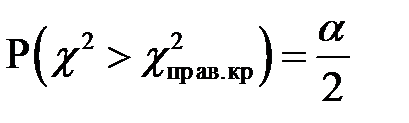 .
.
Левую границу будем искать как правую из условия
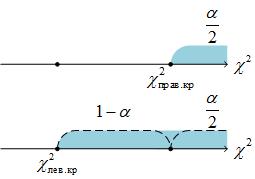
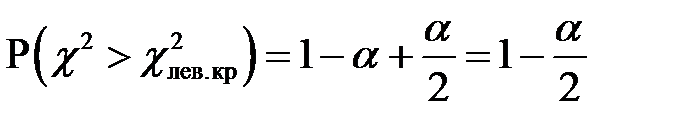 ,
,
то есть 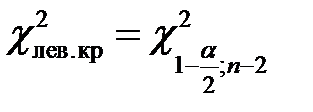 . Отсюда уже находим
. Отсюда уже находим
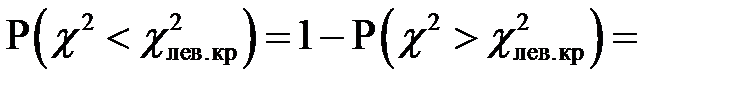
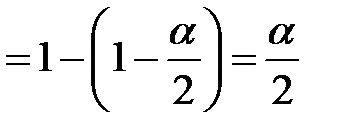 ,
,
то есть
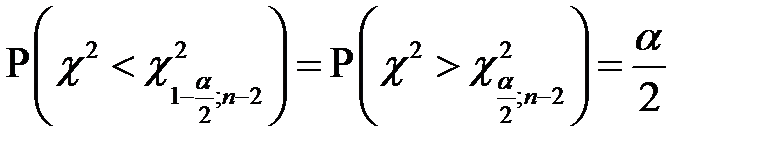 .
.
Тогда
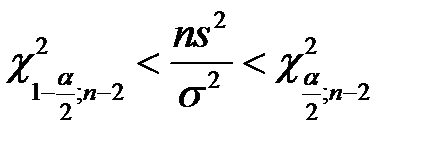 ,
, 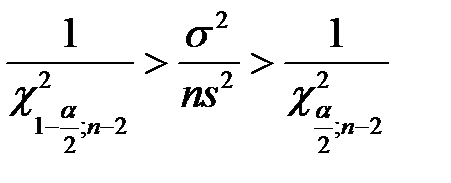 ,
, 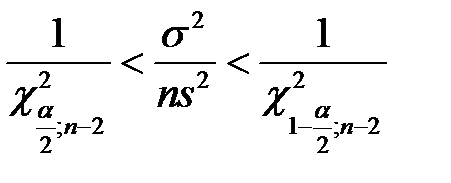 .
.
Умножим на 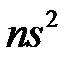 последнее неравенство. Получим
последнее неравенство. Получим
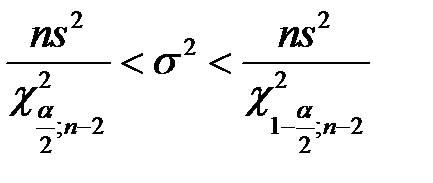 . (К29)
. (К29)
7. Оценка адекватности уравнения регрессии (Коэффициент детерминации)
Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений зависимой переменной от средней имеет вид
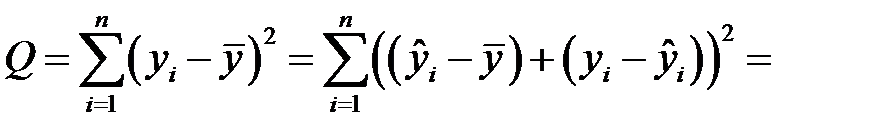
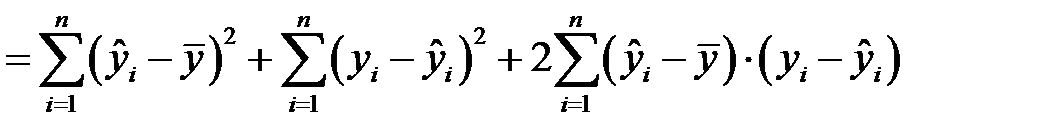 ,
,
где
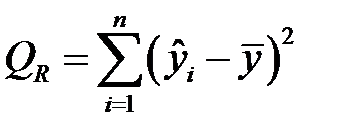 – сумма квадратов, обусловленная регрессией, то есть, факторная сумма квадратов отклонений групповых средних от общей средней;
– сумма квадратов, обусловленная регрессией, то есть, факторная сумма квадратов отклонений групповых средних от общей средней;
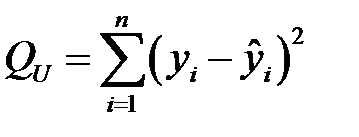 – остаточная сумма квадратов, характеризующая влияние неучтенных факторов, то есть, остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней.
– остаточная сумма квадратов, характеризующая влияние неучтенных факторов, то есть, остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней.
Кроме того, понятно, что сумма
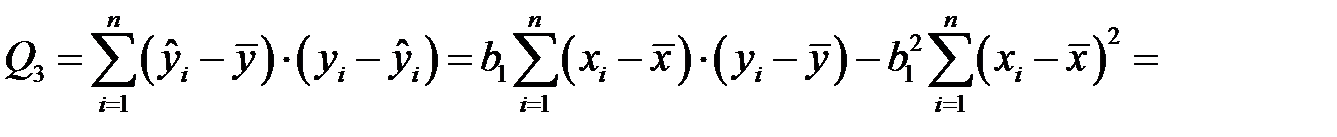
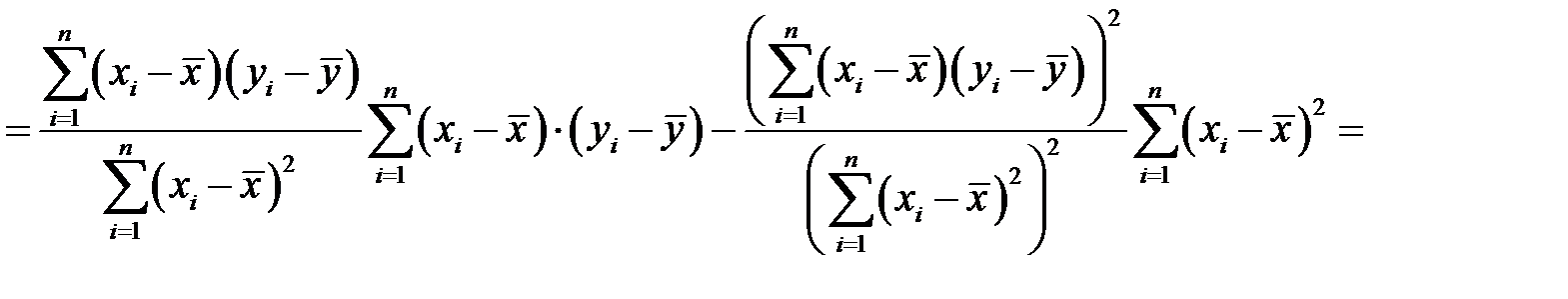
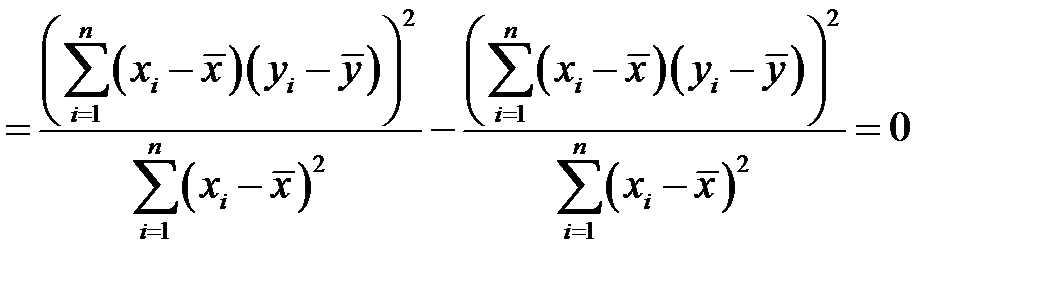 ,
,
ибо
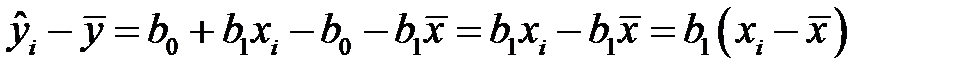
и
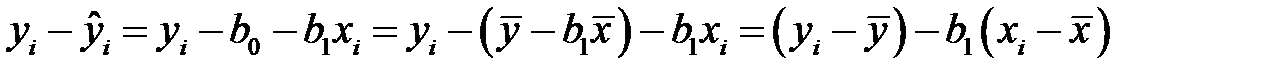 ,
,
где
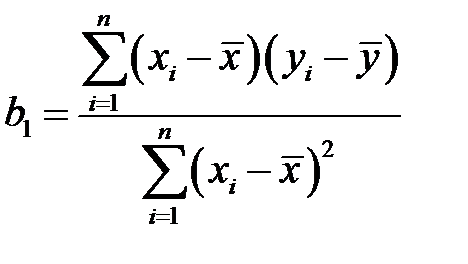 .
.
Таким образом, имеем
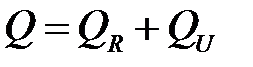 . (К30)
. (К30)
Несмещенные оценки факторной дисперсии
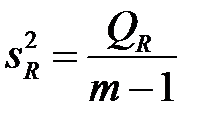 (К31)
(К31)
и остаточной дисперсии
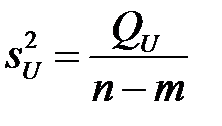 , (К32)
, (К32)
где 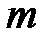 – число оцениваемых параметров уравнения регрессии;
– число оцениваемых параметров уравнения регрессии; 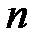 – число наблюдений.
– число наблюдений.
Однофакторный дисперсионный анализ используется для проверки гипотезы о равенстве групповых средних. Гипотеза о равенстве групповых средних
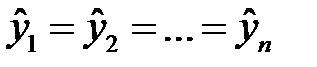
равносильна гипотезе о равенстве факторной и остаточной дисперсий
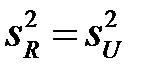 .
.
Равенство групповых средних 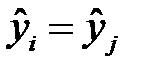 , где
, где 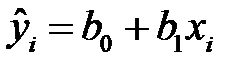 и
и 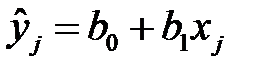 , влечет
, влечет
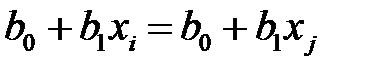 ,
, 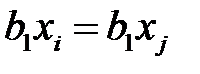 ,
, 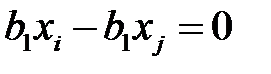 ,
, 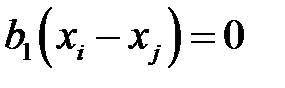 .
.
Поскольку 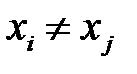 , то
, то 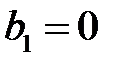 , то есть линейная связь отсутствует. Таким образом, гипотеза о наличии линейной связи равносильно гипотезе о не равенстве групповых средних, которая в свою очередь эквивалентна гипотезе о не равенстве факторной и остаточной дисперсий. Для проверки последней применим критерий Фишера – Снедекора. Случайная величина
, то есть линейная связь отсутствует. Таким образом, гипотеза о наличии линейной связи равносильно гипотезе о не равенстве групповых средних, которая в свою очередь эквивалентна гипотезе о не равенстве факторной и остаточной дисперсий. Для проверки последней применим критерий Фишера – Снедекора. Случайная величина 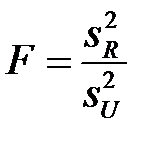 имеет распределение Фишера – Снедекора. По таблице критических точек распределения Фишера – Снедекора, определяем критическое значение
имеет распределение Фишера – Снедекора. По таблице критических точек распределения Фишера – Снедекора, определяем критическое значение 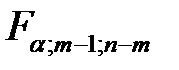 . Гипотезу о не равенстве факторной и остаточной дисперсий принимаем, если
. Гипотезу о не равенстве факторной и остаточной дисперсий принимаем, если
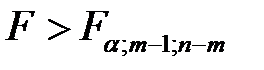 . (К33)
. (К33)
Таким образом, неравенство (К33) является критерием соответствием математической модели, выражающей зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям 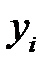 ), характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле
), характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле
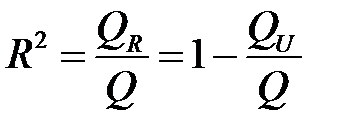 . (К34)
. (К34)
Величина 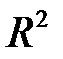 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.
показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.
Так как 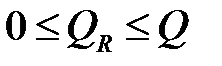 , то
, то 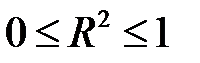 .
.
Чем ближе 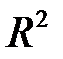 к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линейной регрессии.
к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линейной регрессии.
Если 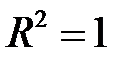 , то эмпирические точки
, то эмпирические точки 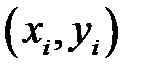 лежат на линии регрессии и между переменными
лежат на линии регрессии и между переменными 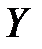 и
и 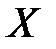 существует линейная функциональная зависимость.
существует линейная функциональная зависимость.
Если 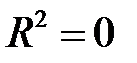 , то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.
, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.
Тогда наблюдаемое значение 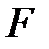 -статистики
-статистики
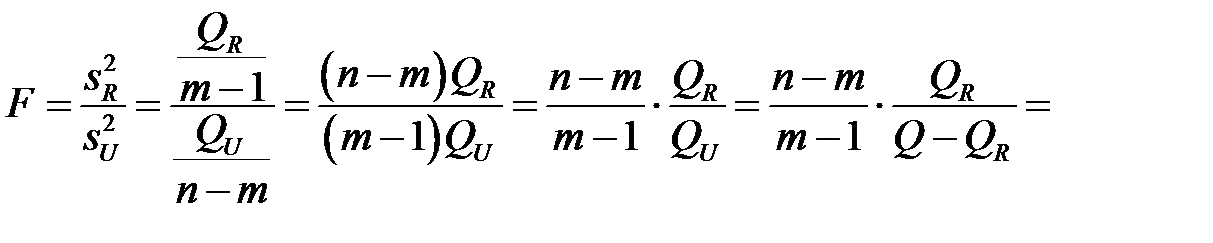
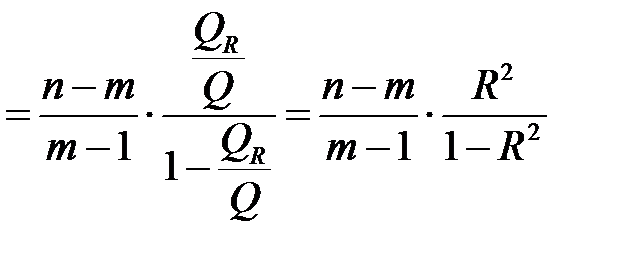 ,
,
таким образом,
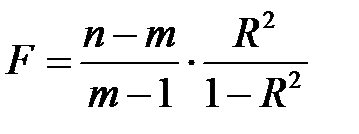 . (К35)
. (К35)
В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, то есть
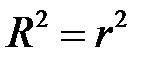 ,
,
ибо учитывая равенства (К10) и (К13), получим
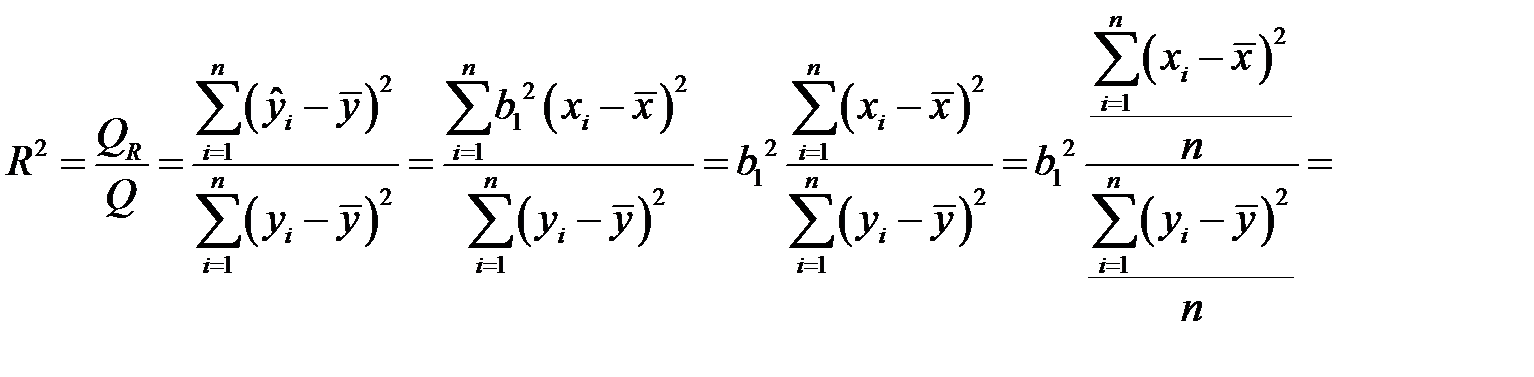
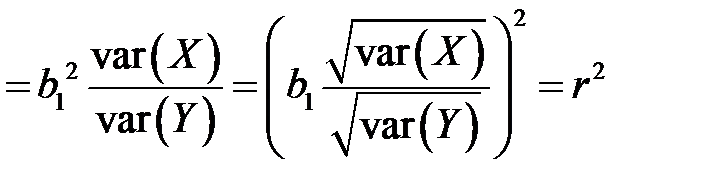 .
.
Дата добавления: 2018-09-24; просмотров: 742;
