Стандартизованные уравнения множественной регрессии.

На практике часто бывает необходимо сравнение влияния на зависимую переменную различных объясняющих переменных, когда последние выражаются разными единицами измерения. В этом случае используют стандартизованные коэффициенты регрессии 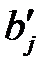и коэффициенты эластичности 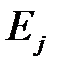, , 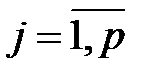определяемые равенствами

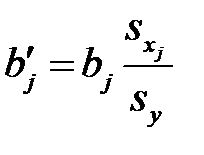, (М14)

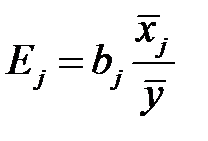, (М15)

где средние квадратические отклонения 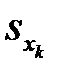, и определяются равенствами

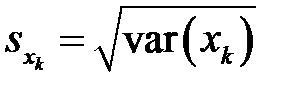и .

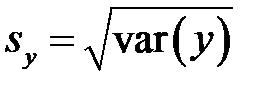Стандартизованный коэффициент регрессии 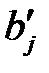показывает, на сколько единиц 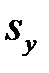изменится в среднем зависимая переменная 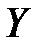при увеличении только -ой объясняющей переменной на 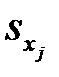единиц.

Коэффициент эластичности 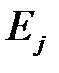показывает, на сколько процентов (от средней) изменится в среднем зависимая переменная 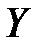при увеличении только -ой объясняющей переменной на один процент.

Для получения стандартизованных уравнений множественной регрессии, переменные, объясняющие и зависимые, нормируют.

Именно, из уравнения (М3) множественной регрессии

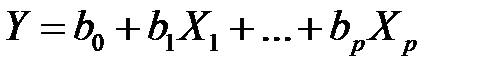, (М16)

получим

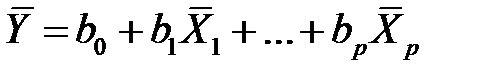. (М17)

Вычитая из равенства (М16) равенство (М17), получим равенство

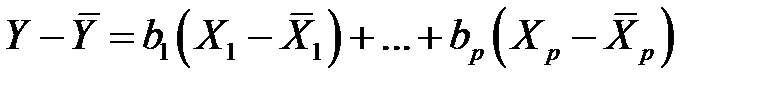, (М18)

которое преобразуем к виду

,

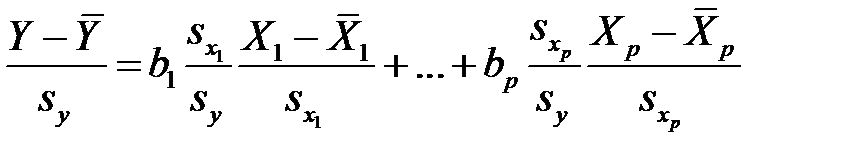или

,

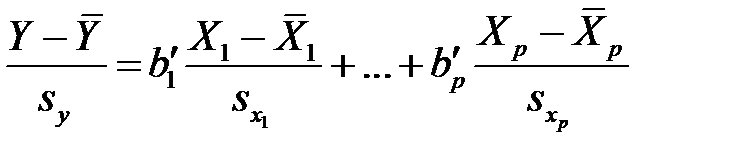где

, …, .

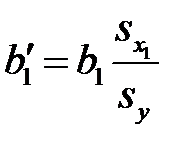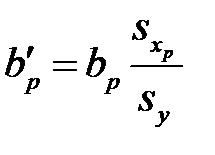Вводя стандартизованные переменные

, , …, ,

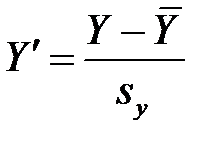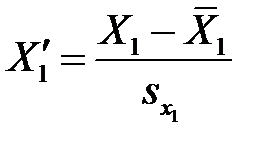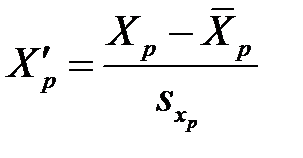получим уравнение

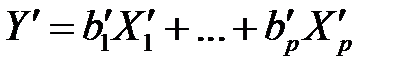. (М19)

Подобным образом, уравнение (М18) запишем в виде

,

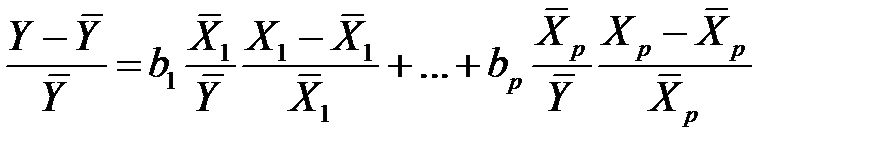или

,

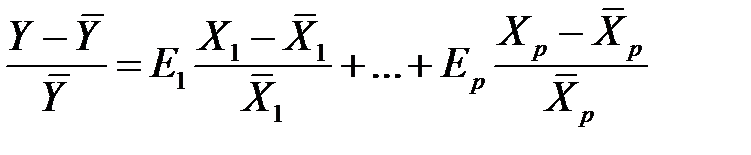где

, …, .

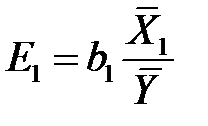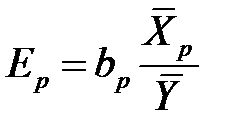Вводя переменные

, , …, ,

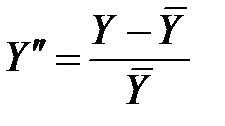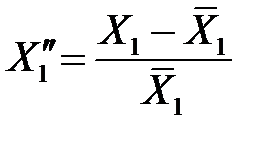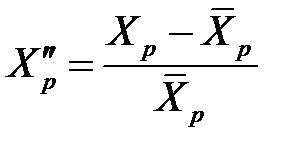приходим к уравнению

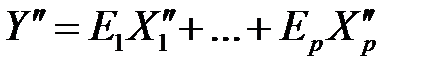. (М20)

Уравнения (М19) и (М20) будем называть стандартизованными уравнениями множественной регрессии.

Пример 1.3. Имеются следующие данные о сменной добыче угля на одного рабочего в тоннах, мощности пласта 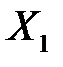в метрах и уровне механизации работ 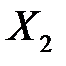в %, характеризующие процесс добычи угля в десяти шахтах (см. пример 1.1). Найти стандартизованные коэффициенты регрессии, коэффициенты эластичности и стандартизованные уравнения множественной регрессии.

Решение. Находим средние квадратические отклонения

,

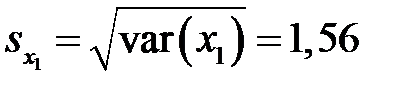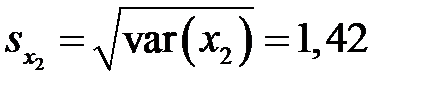
и

.

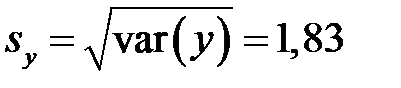Тогда

, .

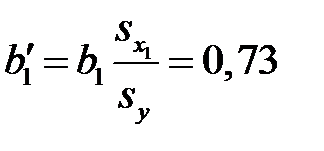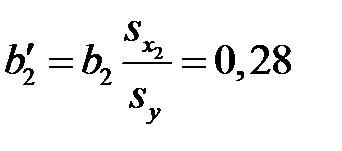Зависимая переменная 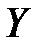изменится в среднем на 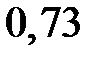единиц 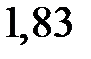при увеличении только объясняющей переменной 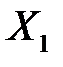на 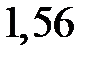единиц.

Стандартизованные коэффициенты регрессии 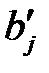тесно связаны с парными коэффициентами корреляции.

Парные коэффициенты корреляции определяются равенствами

,

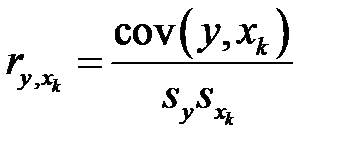а частные коэффициенты корреляции, определяются равенствами

.

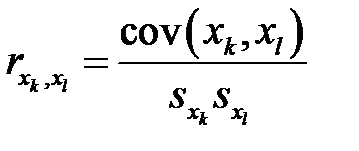Показатели парной корреляции – 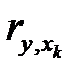характеризуют тесноту связи результата и фактора, не принимая во внимание возможного влияния на результат других факторных признаков. Поэтому во множественном регрессионном анализе возникает проблема определения тесноты связи между двумя признаками в чистом виде, т.е. при устранении воздействия других факторов.

Можно дать следующую качественную интерпретацию возможных значений коэффициента корреляции: если 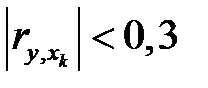– связь практически отсутствует; 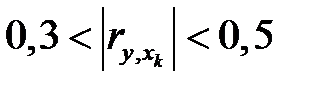– умеренная связь; 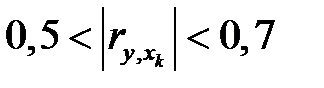– заметная связь; 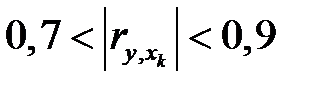– тесная связь; 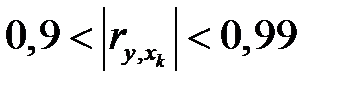– связь весьма сильная.

Теперь делим первое равенство системы (М22) на произведение 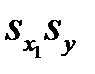. Приходим к равенству

,

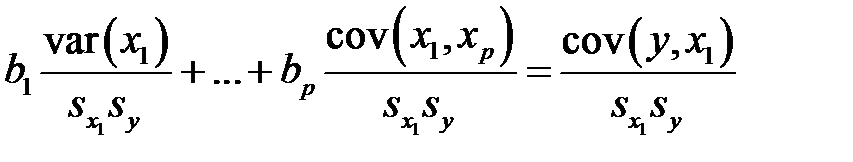которое преобразуем к виду

.

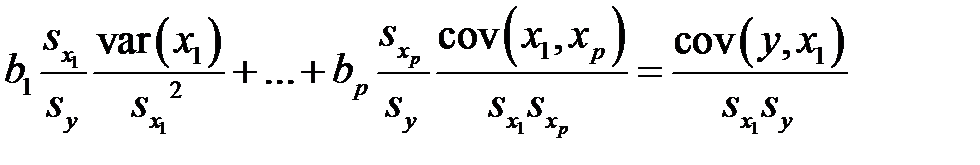Подобным образом поступим с каждым последующим уравнением системы (М22). Для последнего уравнения, делением на произведение 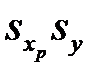, дает равенство

,

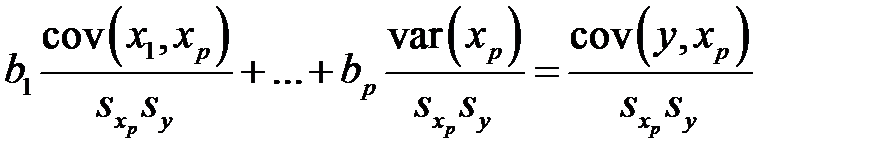которое легко преобразуется к виду

.

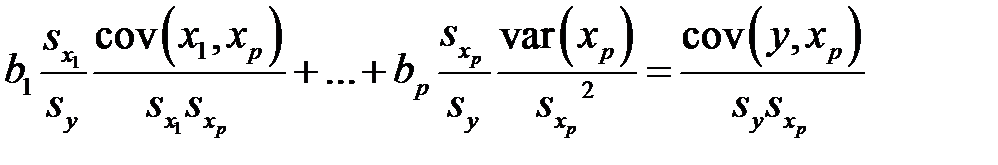Но 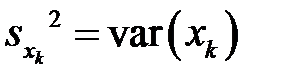. Учитывая также равенства (М14), приходим к системе уравнений

,

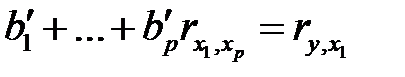. . . . . . . (М24)

.

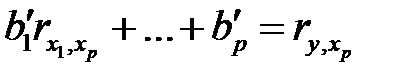Таким образом, стандартизованные коэффициенты регрессии 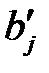являются решением системы (М24).