Мультиколлинеарность
Парные коэффициенты корреляции собирают в матрицу, которую используют для оценки мультиколлинеарности факторов. Матрица парных коэффициентов корреляции зависимой переменной 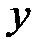 с объясняющими переменными
с объясняющими переменными 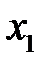 ,
, 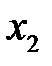 , …,
, …, 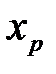 , позволяет оценить степень влияния каждой объясняющей переменной
, позволяет оценить степень влияния каждой объясняющей переменной 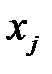 на зависимую переменную
на зависимую переменную 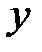 , а также тесноту взаимосвязей факторов между собой. Корреляционная матрица
, а также тесноту взаимосвязей факторов между собой. Корреляционная матрица 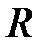 в общем случае имеет вид
в общем случае имеет вид
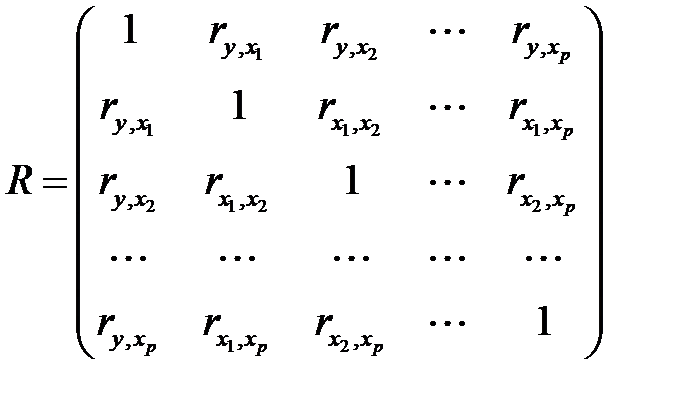 . (М25)
. (М25)
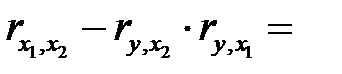
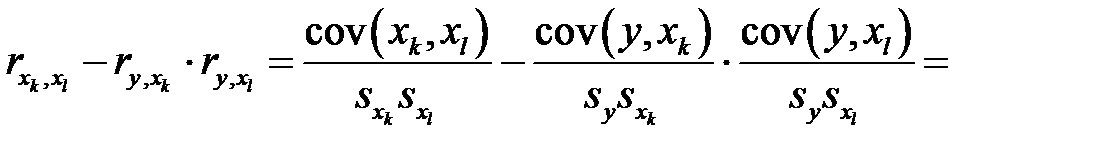
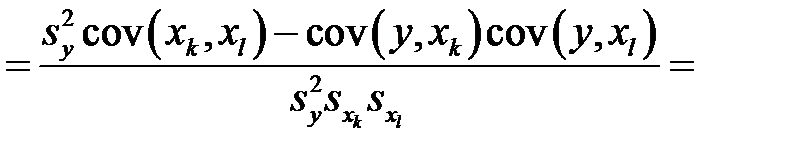
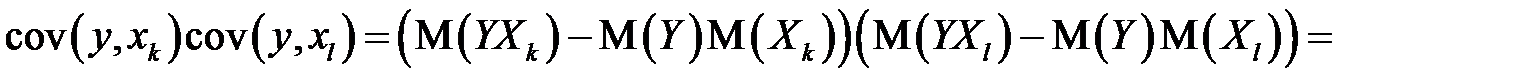
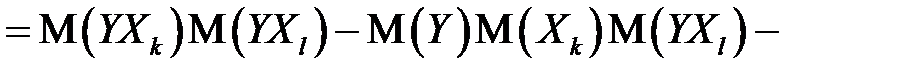
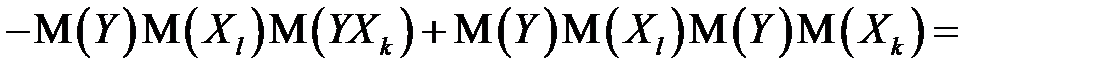
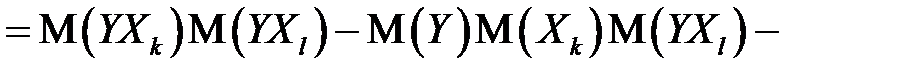
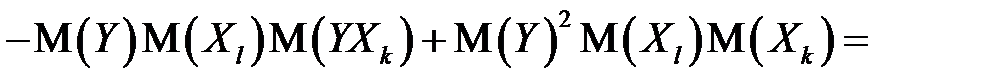
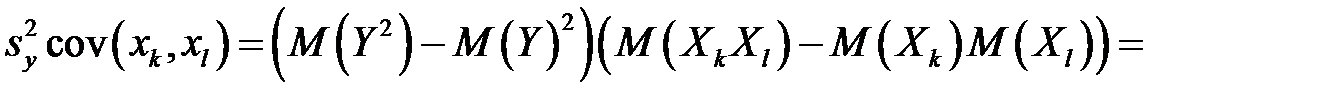
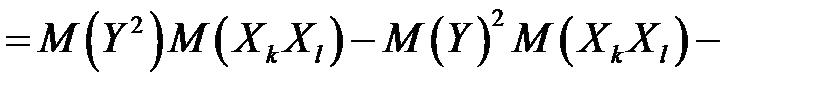
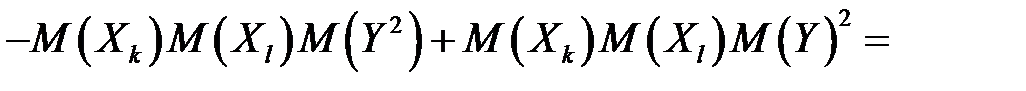
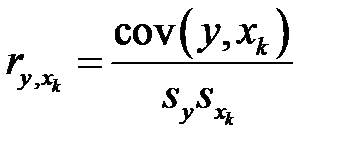 ,
,
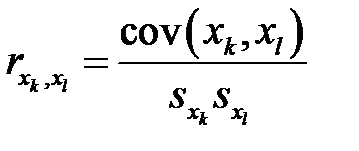 .
.
Матрица симметрична, на ее диагонали стоят единицы. Если в матрице есть межфакторный коэффициент корреляции 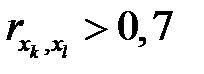 , то в данной модели множественной регрессии существует мультиколлинеарность.
, то в данной модели множественной регрессии существует мультиколлинеарность.
Поскольку исходные данные, по которым устанавливается взаимосвязь признаков, являются выборкой из некой генеральной совокупности, вычисленные по этим данным коэффициенты корреляции будут выборочными, т. е. они лишь оценивают связь. Необходима проверка значимости, которая отвечает на вопрос: случайны или нет полученные результаты расчетов.
Частный коэффициент корреляции характеризует тесноту линейной зависимости между результатом и соответствующим фактором при устранении влияния других факторов. Частный коэффициент корреляции оценивает тесноту связи между двумя переменными при фиксированном значении остальных факторов. Если вычисляется, например, 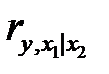 (частный коэффициент корреляции между
(частный коэффициент корреляции между 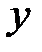 и
и 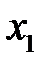 при фиксированном влиянии
при фиксированном влиянии 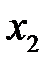 ), это означает, что определяется количественная мера линейной зависимости между
), это означает, что определяется количественная мера линейной зависимости между 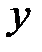 и
и 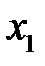 , которая будет иметь место, если устранить влияние
, которая будет иметь место, если устранить влияние 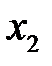 на эти признаки. Если исключают влияние только одного фактора, получают частный коэффициент корреляции первого порядка.
на эти признаки. Если исключают влияние только одного фактора, получают частный коэффициент корреляции первого порядка.
Сравнение значений парного и частного коэффициентов корреляции показывает направление воздействия фиксируемого фактора. Если частный коэффициент корреляции 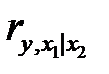 получится меньше, чем соответствующий парный коэффициент
получится меньше, чем соответствующий парный коэффициент 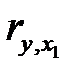 , значит, взаимосвязь признаков
, значит, взаимосвязь признаков 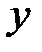 и
и 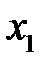 в некоторой степени обусловлена воздействием на них фиксируемой переменной
в некоторой степени обусловлена воздействием на них фиксируемой переменной 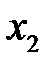 . И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная
. И наоборот, большее значение частного коэффициента по сравнению с парным свидетельствует о том, что фиксируемая переменная 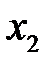 ослабляет своим воздействием связь
ослабляет своим воздействием связь 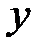 и
и 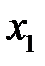 .
.
Частный коэффициент корреляции между двумя переменными ( 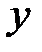 и
и 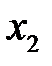 ) при исключении влияния одного фактора (
) при исключении влияния одного фактора ( 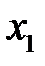 ) можно вычислить по следующей формуле:
) можно вычислить по следующей формуле:
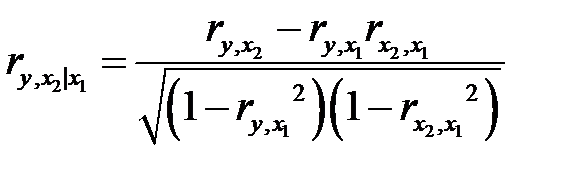 . (М26)
. (М26)
Для других переменных формулы строятся аналогичным образом. При фиксированном 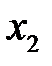
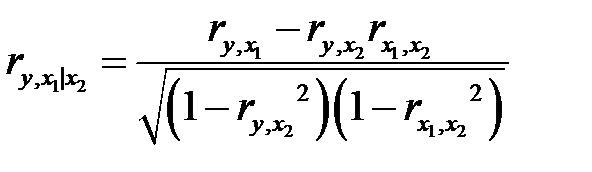 ; (М27)
; (М27)
при фиксированном 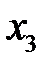
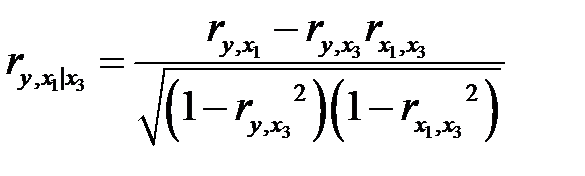 . (М28)
. (М28)
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на переменную 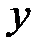 фактора
фактора 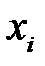 при неизменном уровне других факторов, можно определить по формуле
при неизменном уровне других факторов, можно определить по формуле
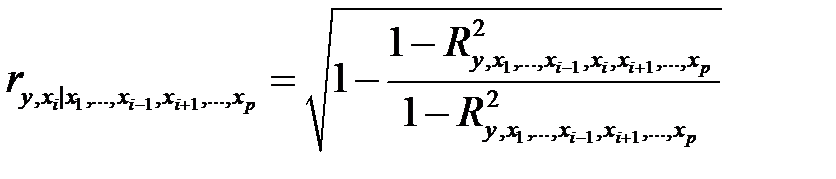
Значимость частных коэффициентов корреляции проверяется аналогично случаю парных коэффициентов корреляции. Единственным отличием является число степеней свободы, которое следует брать равным v = n – l -2, где l – число фиксируемых факторов.
На основании частных коэффициентов можно сделать вывод об обоснованности включения переменных в регрессионную модель. Если значение коэффициента мало или он незначим, то это означает, что связь между данным фактором и результативной переменной либо очень слаба, либо вовсе отсутствует, поэтому фактор можно исключить из модели.
Множественный коэффициент корреляции 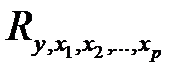 характеризует степень тесноты связи между зависимой переменной
характеризует степень тесноты связи между зависимой переменной 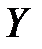 и всеми факторными признаками (предикторами –
и всеми факторными признаками (предикторами – 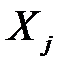 ).
).
На основе корреляционной матрицы R множественный коэффициент корреляции и множественный коэффициент детерминации могут быть исчислены следующим образом:
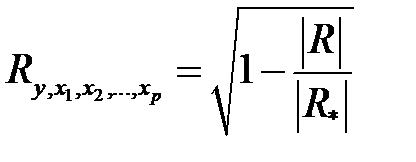 , (М29)
, (М29)
где 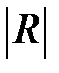 – определитель матрицы парных корреляций,
– определитель матрицы парных корреляций, 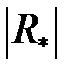 – определитель матрицы парных корреляций, полученной после вычеркивания строки и столбца, представляющих связи зависимой переменной
– определитель матрицы парных корреляций, полученной после вычеркивания строки и столбца, представляющих связи зависимой переменной 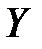 .
.
Частный F-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора 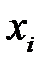 частный F-критерий определится как
частный F-критерий определится как
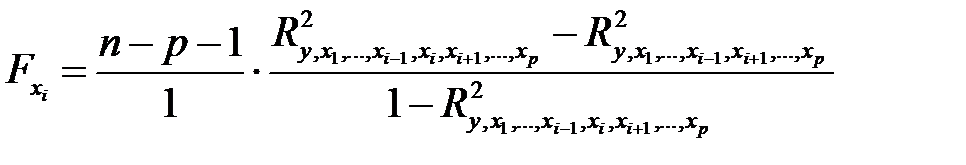
Дата добавления: 2018-09-24; просмотров: 654;
