Мультиколлинеарность и отбор значимых факторов

Мультиколлинеарностью называют высокую взаимную коррелированность объясняющих переменных. Покажем, какие неприятности алгебраического характера это влечет за собой.

Для определения вектора коэффициентов регрессии b используется выражение (3.7): b=(X’X)^-1X’Y, в котором присутствует обратная матрица для X’X.

Пример 4.1.

Дана квадратная матрица А размером 2х2:

.

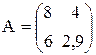Найти обратную ей матрицу А^-1.

Решение.

Формула обращения матрицы:

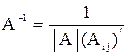
(4.1)

где çA ç = 8×2,9 - 6×4 = 23,2 - 24 = - 0,8 - определитель матрицы А;

(Aij) - матрица, составленная из алгебраических дополнений матрицы А:

;

.

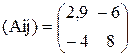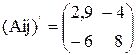Окончательно

.

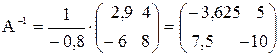Проверим правильность обращения матрицы А. Должно выполняться равенство: АА^-1 = Е, где Е - единичная матрица:

.

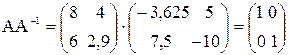В результате проверки получена единичная матрица, что и требовалось показать.

Обратим внимание на то, что матрица А достаточно близка к особенной. Действительно, если бы элемент а₂₂ равнялся не 2,9, а 3,0, то определитель çА ç = 0, деление на 0 невозможно, А^-1 не существует. Обратим также внимание на то, что при а₂₂ =3,0 столбцы линейно зависимы: второй столбец получается из первого делением на 2: А₂=А₁/2. Это случай функциональной зависимости. Нарушается предпосылка-6 множественной регрессии.

На практике чаще бывают случаи, когда взаимосвязь между переменными Х₁, Х₂, ... , Х_p носит статистический характер. При высокой взаимной коррелированности объясняющих переменных определитель квадратной матрицы X’X может очень близко приближаться к нулю. А поскольку вектор оценок b и его ковариационная матрица å_b пропорциональны (X’X)^-1X’Y, получаются большие средние квадратические отклонения коэффициентов b и оценка их по t-критерию Стьюдента не имеет смысла, хотя в целом по F-критерию модель может быть значимой.

При высокой мультиколлинеарности оценки становятся очень чувствительными к малым изменениям наблюденных данных, включая объем выборки. Уравнение регрессии содержательно не интерпретируется, так как некоторые его коэффициенты могут иметь неверные с точки зрения экономической теории (смысла) знаки и неоправданно большие значения.

Существуют различные подходы, в том числе и эвристические, к выявлению и снижению степени мультиколлинеарности.

Первый подход основан на анализе корреляционной матрицы между объясняющими переменными. Признак мультиколлинеарности здесь - наличие парных коэффициентов корреляции со значениями от ç0,7ç и выше. Трудно проследить цепочку взаимозависимости между переменными. Обычно это удается для числа переменных не более 4-х. Некоторые из тесно связанных между собой объясняющих переменных исключаются из списка претендентов, а вместо них могут включаться другие. И так несколько раз.

Второй подход - находить коэффициенты детерминации одной из объясняющих переменных в зависимости от групп других объясняющих переменных. Признак мультиколлинеарности здесь - наличие коэффициента детерминации со значением больше 0,6. Для снижения мультиколлинеарности такие группы переменных исключаются. Вместо них в соответствии с гипотезой о данном явлении вводятся другие переменные. Процедура может повторяться.

Третий подход - исследование матрицы X’X. Если ее определитель близок по модулю к нулю (это еще зависит и от единиц измерения), например, çX’Xç = 0,000013, то это может свидетельствовать о наличии мультиколлинеарности. Далее можно применить эффективную процедуру отбора значащих факторов, которую назовем методом вращения факторов. В качестве основного критерия уместно использовать остаточную дисперсию - несмещенную выборочную оценку s² параметра s² возмущений e:

/.

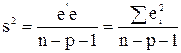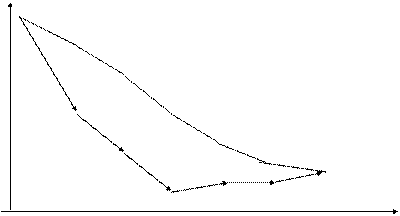
Опишем процедуру отбора факторов методом вращения подробно. Пусть из теоретических соображений для объяснений изменения Y мы отобрали 6 объясняющих факторов-претендентов. Проверка показала высокую мультиколлинеарность. В произвольном порядке присваиваем переменным имена (для удобства буквенные): X_a, X_b, X_c, X_d, X_e, X_f. Затем строим шесть уравнений регрессий с факторами: (X_a), (X_a, X_b), (X_a, X_b, X_c), (X_a, X_b, X_c, X_d), (X_a, X_b, X_c, X_d, X_e), (X_a, X_b, X_c, X_d, X_e, X_f). Для каждого уравнения вычисляем остаточную дисперсию s² и откладываем эти значения на графике рис. 4.1, верхняя ломаная. Как видно, каждая новая переменная, включенная в регрессию по порядку, примерно на одинаковую величину уменьшает остаточную дисперсию. Вывод: все факторы примерно одинаково значимы, и в уравнение нужно включить их все.

	s2
D(Y)		a
		b
	c		c
				d
		e			e	f
					d
			f	a	b
		1 2

Рис. 4.1. Схема отбора значимых факторов

Картина резко меняется, если поступить иначе. Отбираем самый информативный фактор на 1-е место. Для этого строим шесть парных регрессий и для каждой вычисляем остаточную дисперсию s². В искомое уравнение включаем тот фактор, у которого наименьшая дисперсия s². В нашем примере это Х_с. Далее ищем второй по значимости фактор. Для этого строим пять регрессий с парами факторов, один их которых присутствует всегда - Х_с. Для каждой такой регрессии также вычисляем остаточные дисперсии s². В примере наименьшую дисперсию дает фактор Х_е, и т.д.

В работе [5, с. 111] в подобной процедуре в качестве критерия используется 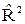- скорректированный коэффициент детерминации.

Вывод: факторы по значимости резко разделились на две группы. Из шести мы отобрали три фактора, которые в совокупности дают небольшую дисперсию ошибки и практически полностью исключают коллинеарность. Заметим, что полное ее исключение обычно и не является целью исследования.