Примеры функций эластичности
| Функция регрессии | Производная регрессии | Функция эластичности |
| Линейная y =bo + b1x+ e | b1 | E= b1x/(bo + b1x) |
| Парабола второго порядка y =bo + b1x+ b2x2+ e | b1+ 2b2x | E=(b1+ 2b2x)x/(bo + b1x+ b2x2) |
| Гипербола y =bo + b1/x+ e | -b1/x2 | E=-b1/(box+b1) |
По определению частной функцией эластичности Еxi(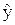 
) множественной регрессии 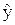=f(x1, x2, ... , xр) является функция
.
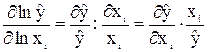Итак, функция эластичности имеет вид:
Еxi( ) =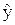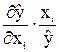 
| (4.3) |
Пример 4.2.
Дано линейное уравнение регрессии 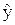=5+6x1-2x2, выборочные средние: 
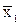=10, 
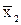=20,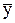 
=25. Найти частную функцию эластичности по переменной х2.
Решение.
По формуле (4.3) искомая функция: Еx2( 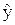) = ¶ 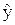/¶x2 ×x2/ 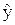= -2x2/(5+6x1-8x2). Можно положить 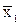=10, и получим частную функцию эластичности Е(x2)= -2x2/(65-8x2). Наконец, для 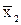=20 можно получить средний частный коэффициент эластичности 
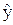по x2: 
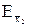=-0,89%. Итак, в окрестности выборочных средних увеличение x2 на 1% приводит к уменьшению 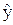на 0,89%.
Пример 4.3.
Дано парное уравнение регрессии со степенной функцией: 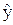=5×х1/2. Найти функцию и средний коэффициент эластичности.
Решение.
Еx( )=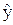 
= 
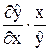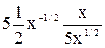= 0,5.
Итак, функция эластичности для степенной функции есть константа.
Дата добавления: 2019-10-16; просмотров: 421;