Оценка значимости и адекватности множественной регрессии
Как и в случае парной регрессии оценить значимость множественной регрессионной модели - значит подтвердить или опровергнуть суждение о том, что эта модель соответствует наблюденным данным.
Для решения задачи также используется дисперсионный анализ, согласно которому для сумм квадратов отклонений справедливо равенство: Q = QR + Qe.
Для этих сумм квадратов нетрудно записать матричные выражения:
Q = å (yi - 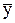 )2 = å yi2-(å yi)2/n = Y ' Y - n )2 = å yi2-(å yi)2/n = Y ' Y - n 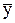 2, 2,
| (3.19) |
Qe = å (yi - 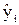 )2 = Y'Y – b' X 'Y, )2 = Y'Y – b' X 'Y,
| (3.20) |
QR = Q - Qe = b'X'Y - n 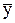 2. 2.
| (3.21) |
Гипотеза Но о равенстве нулю всех параметров модели (b1=b2= ... = bр = 0) отвергается, если фактическое значение статистики Фишера-Снедекора больше ее табличного значения:
F = 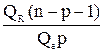 > Fa, p, n-p-1. > Fa, p, n-p-1.
| (3.22) |
Ранее в выражении (2.36) для оценки адекватности, прогностической силы парной регрессионной модели вводился коэффициент детерминации:
R2 = QR / Q = 1 - Qe / Q .
Для множественной регрессии коэффициент R2 может быть рассчитан по формулам:
R2 = QR / Q = 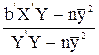
| (3.23) |
| или | |
R2 = 1 - Qe / Q = 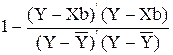
| (3.24) |
| или | |
R2 = 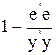
| (3.25) |
где e = Y - Xb, 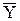 = ( = ( 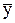 , , 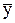 , ... , ... 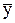 ), y =(Y - ), y =(Y - 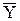 ) - n -мерные векторы ) - n -мерные векторы
|
e'e = å ei2 = å (yi - 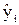 )2 )2
|
y'y = å (yi - 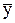 )2. )2.
|
Несмотря на достоинства коэффициента детерминации R2, судить только по нему о качестве - адекватности - модели некорректно. Дело в том, что R2 растет с увеличением числа объясняющих переменных, включаемых в модель, что не всегда верно. Поэтому применяют скорректированный (адаптированный) коэффициент детерминации 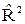 :
:
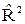 = = 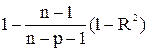 . .
| (3.26) |
или
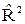 = = 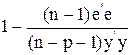 . .
| (3.27) |
Как видно, чем больше объясняющих переменных р, тем меньше 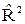 в сравнении с R2 при прочих равных условиях. Таким образом, в модель должны включаться только те объясняющие переменные, которые действительно информативны и существенно влияют на объясняемую переменную Y.
в сравнении с R2 при прочих равных условиях. Таким образом, в модель должны включаться только те объясняющие переменные, которые действительно информативны и существенно влияют на объясняемую переменную Y.
Вопросы для самоконтроля
1. Запишите произвольный числовой пример линейной модели множественной регрессии для р=2 и n=5.
2. Какая модель называется классической нормальной ЛММР?
3. В чем смысл оптимальности b из уравнения (3.4)?
4. Является ли оценка b по МНК в множественной регрессии эффективной?
5. Что показывает стандартизованный коэффициент регрессии bj’?
6. Что показывает средний коэффициент эластичности 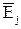 ?
?
7. Сколько элементов содержит ковариационная матрица для СВ (Х, Y)?
8. Что означает åb в выражении (3.10), приведите произвольный числовой пример такой матрицы.
9. На произвольном числовом примере раскройте смысл математических объектов: s2, e, e’, p, ei.
10. В чем состоит гипотеза Но при оценке значимости уравнения множественной регрессии?
11. В чем преимущество скорректированного коэффициента детерминации перед обычным коэффициентом?
Практические вопросы построения регрессионных моделей
Дата добавления: 2019-10-16; просмотров: 503;
