Выборочные оценки и доверительные интервалы
В многомерном регрессионном анализе матричным аналогом дисперсии одной переменной является ковариационная матрица åb вектора оценок параметров b:
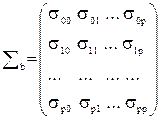 ,
,
где sij = M[(bi-M(bi))×(bj-M(bj))] - ковариации (корреляционные моменты) оценок параметров bi и bj . На главной диагонали этой матрицы находятся дисперсии оценок параметров регрессии:
sii = M[(bi-M(bi))×(bi-M(bi))] = sbi2.
Путем преобразований (см. [5, с. 92]) получаем ковариационную матрицу:
| åb =s2(Х’X)-1. | (3.10) |
Таким образом, с помощью обратной матрицы (Х’X)-1 определяется как сам вектор оценок b, так и дисперсии-ковариации его компонент.
Выше мы показали, что оценка b вектора b по МНК является несмещенной и обладает наименьшей дисперсией, т.е. является эффективной (“наилучшей”).
Рассмотрим оценку дисперсии s2 возмущений e=Y – Xb (подробный вывод см. [5, с. 95]). Соответствующее выражение для несмещенной выборочной оценки s2 параметра s2 возмущений e:
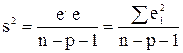 . .
| (3.11) |
Оценим значимость коэффициентов bj множественной регрессии, а затем и доверительного интервала для них.
Нулевая гипотеза Но: b= 0 отвергается с уровнем значимости a, если:
| çt ç= çbj - bjç / sbj > t1-a, n-p-1 sbj. | (3.12) |
Поэтому доверительный интервал для параметра bj:
| bj - t1-a, n-p-1 sbj £ bj £ bj + t1-a, n-p-1 sbj. | (3.13) |
Аналогично доверительному интервалу (2.26) для Мх(Y) парной регрессии построим доверительный интервал для условного МО Мх(Y) множественной регрессии:
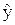 - t1-a, k - t1-a, k 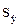 £ Mx(Y) £ £ Mx(Y) £ 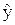 + t1-a, k + t1-a, k 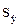 , ,
| (3.14) |
где 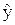 - групповая средняя, определяемая по уравнению регрессии;
- групповая средняя, определяемая по уравнению регрессии;
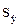 = = 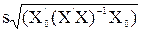 - стандартная ошибка групповой средней - стандартная ошибка групповой средней 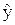 ; ;
| (3.15) |
| Хо' = (1 x10 x20 ... xp0) - вектор значений объясняющих переменных. |
На основе выражения (3.14) можно оценивать ошибку (конус) прогноза в среднем.
Однако индивидуальное значение прогноза имеет больший доверительный интервал. Ранее мы рассмотрели его для парной регрессии (см. формулу (2.28)). Аналогичный интервал для индивидуальных значений зависимой переменной  множественной регрессии:
множественной регрессии:
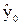 - t1-a, n-p-1 - t1-a, n-p-1 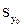 £ £  £ £ 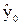 + t1-a, n-p-1k + t1-a, n-p-1k 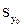 , ,
| (3.16) |
где 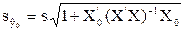 . .
| (3.17) |
Аналогично доверительному интервалу для s2 парной регрессии (2.31) строится доверительный интервал и для множественной регрессии с соответствующим изменением числа степеней свободы для c2:
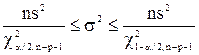 . .
| (3.18) |
Дата добавления: 2019-10-16; просмотров: 550;
