Схема дисперсионного анализа
| Вид дисперсии | Сумма квадратов | Число степеней свободы | Средние квадраты (дисперсии) |
| Регрессия | QR = å ( 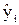 - - 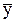 2 2
| m-1 | 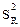 = QR / (m-1) = QR / (m-1)
|
| Остаточная | Qe = å ( 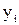 - - 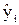 )2 )2
| n-m | s2 = Qe / (n-m) |
| Общая | Q = å ( 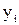 - - 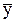 )2 )2
| n-1 |
Примечание: в графе 4 средние квадраты являются несмещенными оценками соответствующих дисперсиий.
Из схемы дисперсионного анализа: уравнение регрессии будет значимо на уровне a, если фактическое значение статистики F больше его табличного значения (отвергаем нулевую гипотезу Но о незначимости регрессии и принимаем конкурирующую с ней гипотезу Н1 о значимости):
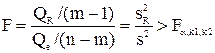 , ,
| (2.33) |
где Fa,k1,k2 - табличное (критическое) значение F-критерия Фишера-Снедекора для уровня значимости a, степеней свободы k1 = m-1, k2 = n-m.
Смысл статистики F прозрачен: его значение показывает, во сколько раз объясненная регрессией дисперсия 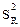 СВ
СВ 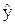 больше остаточной (необъясненной) дисперсии s2 СВ е. Чем больше это отношение, тем более значимо уравнение регрессии.
больше остаточной (необъясненной) дисперсии s2 СВ е. Чем больше это отношение, тем более значимо уравнение регрессии.
Для парной регрессии m=2 и критерий Фишера-Снедекора формулируется так:
уравнение значимо, если 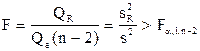 . .
| (2.34) |
Значимость уравнения парной регрессии можно равносильно оценить и иначе, по коэффициенту регрессии b1. Действительно, если нулевая гипотеза Но состоит в том, что b1 незначимо отличается от 0, и она подтверждается, то прямая регрессии расположена параллельно оси ОХ: объясняющая переменная Х ничего не объясняет. И наоборот: если b1 значимо отличается от 0, значит и все уравнение парной регрессии значимо.
Соответствующий критерий на основе статистики Стьюдента:
Но: b1=0 отвергается, если çt ç = ç 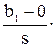 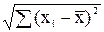 ç > t1-a,n-2. ç > t1-a,n-2.
| (2.35) |
Равносильность критериев для парной регрессии вытекает из их функциональной связи: F=t2.
Иногда эконометристу требуется оценить значимость коэффициента корреляции. Соответствующий критерий:
Но: r=0 отвергается, если çt ç =çr ç 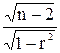 > t1-a,n-2. > t1-a,n-2.
| (2.36) |
В теории и практике эконометрики используется еще один критерий качества регрессионной модели - коэффициент детерминации:
| R2 = QR/Q = 1 - Qe/Q. | (2.37) |
Очевидно, что 0£QR£Q. Отсюда свойство коэффициента детерминации: 0 £ R2 £ 1. Значение R2 показывает, какую долю составляет вариация регрессионной переменной по отношению к общей вариации объясняемой переменной. Ясно, что чем ближе R2 к 1, тем регрессионная модель более адекватна, имеет большую прогностическую силу, лучше подходит к наблюденным данным.
Критерий значимости уравнения регрессии (2.33) можно эквивалентно записать с помощью коэффициента детерминации:
F = 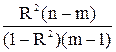 > Fa,k1,k2. > Fa,k1,k2.
| (2.38) |
Для парной регрессии коэффициент детерминации равен квадрату коэффициента корреляции: R2 = r2.
Вопросы для самоконтроля
1. В чем суть метода наименьших квадратов, наименьших модулей, в чем преимущество первого перед вторым?
2. В чем различия между параметрами bо, b1 и bo, b1?
3. Что общего и в чем отличие коэффициента r и ковариации Cov(Х, Y)?
4. Какой вывод следует из того, что r=0?
5. Приведите числовой пример выборки (хi,уi) из 6 пар.
6. Назовите пять предпосылок, которым должна отвечать нормальная классическая линейная регрессионная модель.
7. Дайте определения типам оценок: несмещенная, состоятельная, эффективная. Являются ли эти оценки независимыми?
8. Какими свойствами обладают оценки bo и b1 по теореме Маркова?
9. В чем смысл метода максимального правдоподобия?
10. Определите понятия: доверительная вероятность, доверительный интервал.
11. Раскройте смысл понятия доверительного интервала для среднего 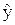 (х).
(х).
12. Раскройте смысл понятия доверительного интервала для индивидуального значения 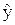 (х).
(х).
13. Для оценки точности прогноза какой из двух типов доверительных интервалов вы выберете?
14. Верно ли суждение: чем больше уровень значимости, тем больше доверительный интервал?
15. Раскройте смыcл понятия: оценка значимости регрессии.
16. Проверьте истинность равенства (2.32) Q = QR + Qe для выборок Х=(2, 4, 6, 9) и Y=(1, 5, 6, 12).
17. Раскройте смысл выражения: Но: b1=0.
18. Каким образом коэффициент детерминации R2 характеризует значимость регрессии?
Дата добавления: 2019-10-16; просмотров: 498;
