Сравнение влияния объясняющих переменных

При исследовании явления с помощью модели множественной регрессии часто бывает необходимым сравнить влияние объясняющих переменных на зависимую переменную. Иногда это можно сделать прямо по значениям коэффициентов регрессии b_i. Однако чаще всего они имеют разную размерность и их влияние трудно сопоставить. Поэтому используют стандартизованные коэффициенты регрессии b_j’ и коэффициенты (или функции) эластичности E_j (j=1, 2, ... , p):

и

.

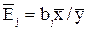(3.9)

Стандартизованный коэффициент регрессии b_j’ показывает, на сколько величин s_y изменится в среднем зависимая переменная Y при увеличении только j-й объясняющей переменной на s_xj.

Средний коэффициент эластичности 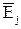показывает, на сколько процентов изменится в среднем Y при увеличении одной переменной x_j в окрестности значения 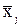на 1%.

Пример 3.1. На основе данных примера 2.1, табл. 2.2 для регрессии 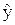=76,88-0,35x рассчитать и раскрыть смысл стандартизованного коэффициента b₁’ и коэффициента эластичности E₁.

Решение. По формуле (3.8) b₁’ = b₁ s_x1 / s_y = -0,35×5,86 / 5,84 = -0,35 (в нашем случае значение практически не изменилось). Итак, при увеличении среднесуточного дохода х₁ на s_x1 =5,86 (руб.) доля расходов на питание 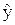уменьшится на 0,35 (%). Заметим, что в данном примере объясняемая переменная измеряется в процентах по условию.

Коэффициент эластичности: 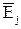= b_j 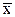/ 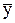= -0,35×54,9/57,89 = -0,33. Таким образом, при увеличении суточного дохода на 1% доля расхода на питание сокращается на 0,33%.