Дискретная линейная свертка

Во временной области соотношение вход-выход ЛДС в случае использования импульсной характеристики может быть описано формулой дискретной линейной свертки:

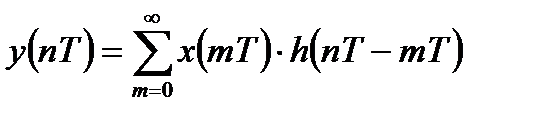(1.1)

или

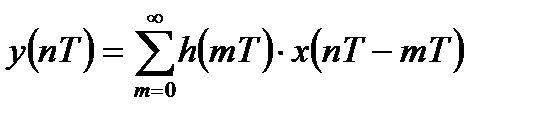. (1.2)

Для физически реализуемой системы импульсная характеристика 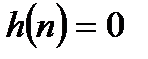при 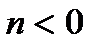, поэтому выражения для дискретной линейной свертки за счет замены верхнего индекса суммирования на 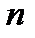изменятся следующим образом:

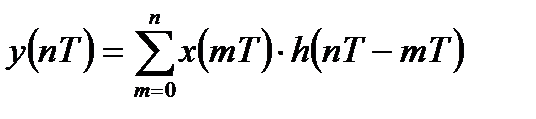(1.3)

или

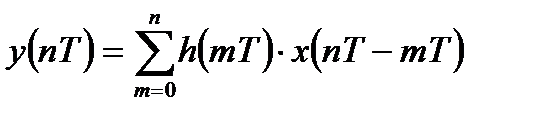. (1.4)

Такая запись означает, что ЛДС при вычислении очередного отсчета оперирует только прошлыми значениями входного сигнала и еще ничего не знает о будущих входных отсчетах.

Если последовательност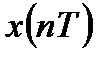и и 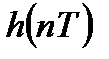являются конечными и имеют длительност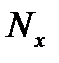и и 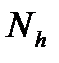, соответственно, то выходная последовательность 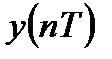также дееется конечной с длительностью 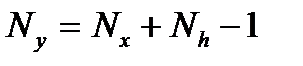. Например, при использовании в дчестве входного сигнала единичного импульса длительностью 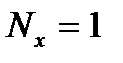, как и ожидалось, длительность выходного сигнала определяется длительностью импульсной характеристики: .

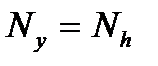Соответственно, линейная свертка конечных последовательностей с длинам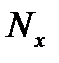и и 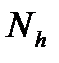определяется выражением:

, .

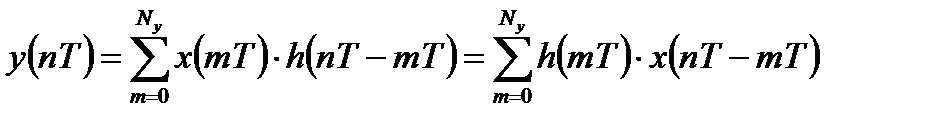где .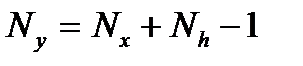

Последовательност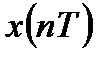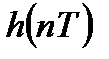и , и 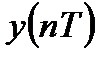равны нулю вне интервала длительностью .

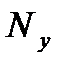Дискретная линейная свертка является дискретным аналогом интеграла свертки (Дюамеля) линейных аналоговых систем. Однако в отличие от интеграла Дюамеля, который исключительно является инструментом анализа, дискретная линейная свертка дополнительно выполняет важную функцию алгоритма обработки входных цифровых сигналов. В данной лекции рассматриваются свойства дискретной линейной свертки именно как алгоритма.

Дискретная линейная свертка при формировании одного отсчета выходного сигнала может быть представлена в виде скалярного произведения двух векторов:

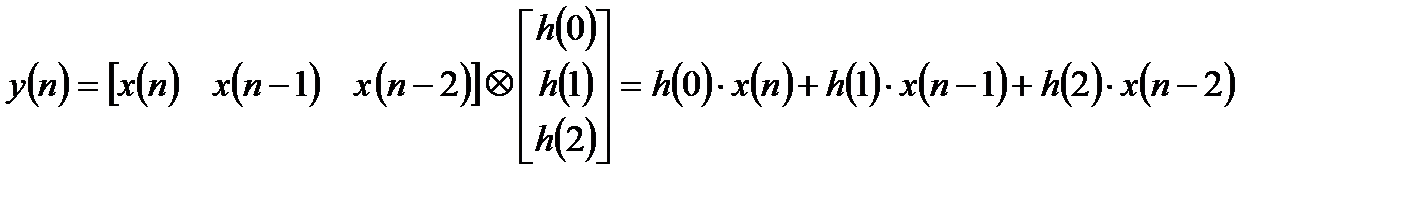. (1.5)

При расчете нескольких последовательных отсчетов выходного сигнала необходимо использовать различные векторы входных сигналов, соответствующие различным выходным отсчетам. Если эти различные вектора входных сигналов определенным образом организовать в матрицу, то выходной сигнал ЛДС может быть получен в результате матрично-векторного умножения:

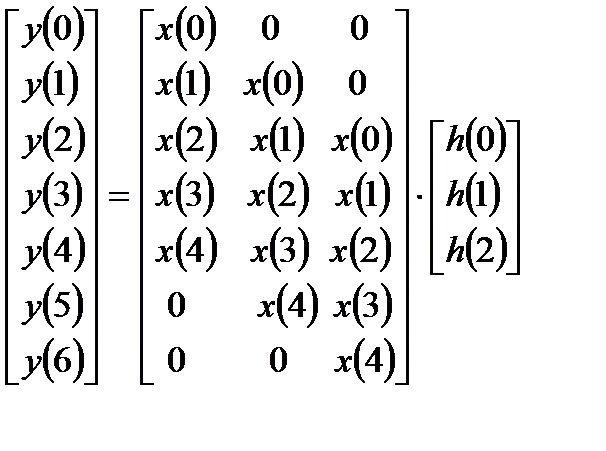. (1.6)

Матрица, составленная из разных векторов входного сигнала, называется матрицей свертки (convolution matrix):

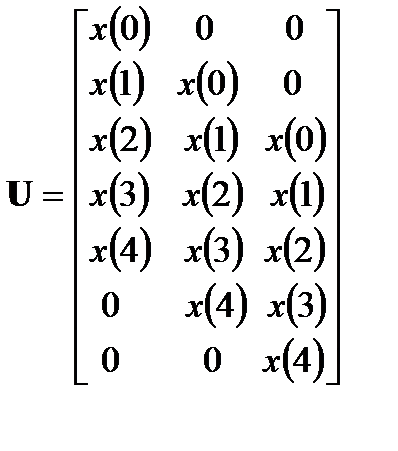. (1.7)

С точки зрения технической реализации линейная свертка представляет собой трансверсальный фильтр или фильтр с конечной импульсной характеристикой (КИХ фильтр). Структурная схема трансверсального фильтра, осуществляющего линейную свертку сигналов, приведена на рисунке 1.1:

Рисунок 1.1 – Схема трансверсального фильтра, осуществляющего линейную свертку сигналов.