Синтез нерекурсивных фильтров методом окон
Для данного метода задается желаемый коэффициент передачи в виде непрерывной периодической функции, определенной в диапазоне частот от нуля до частоты Найквиста 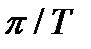 :
:
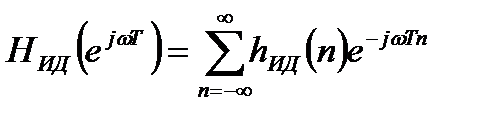 . (2.1)
. (2.1)
Рисунок 2.1 – идеальная АЧХ ПФ
Вычисляется обратное преобразование Фурье, полученное в предположении периодичности функции, которое дает бесконечную последовательность отсчетов идеальной импульсной характеристики в виде коэффициентов ряда Фурье:
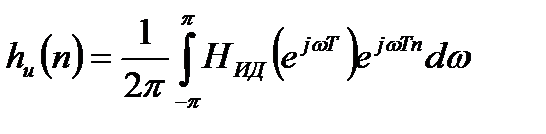 . (2.2)
. (2.2)
Рисунок 2.2 – процедура усечения импульсной характеристики
Для получения реализуемого нерекурсивного фильтра заданного порядка эта бесконечная последовательность усекается. В результате усечения получается частотная характеристика синтезированного фильтра:
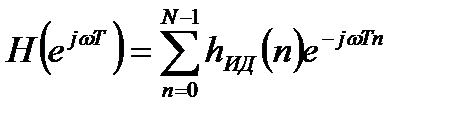 . (2.3)
. (2.3)
После замены 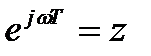 получим передаточную функцию цифрового фильтра:
получим передаточную функцию цифрового фильтра:
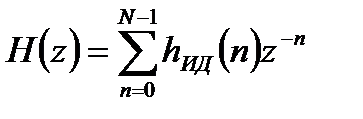 . (2.4)
. (2.4)
Рисунок 2.3 – искажения частотной характеристики
Из-за усечения первоначально заданная частотная характеристика искажается. В результате появляются:
- переходные полосы между областями пропускания и задерживания;
- пульсации 9% на границах полос пропускания и задерживания (явление Гиббса);
- колебания коэффициента передачи в полосах пропускания;
- в полосах задерживания АЧХ принимает лепестковый характер.
Для ослабления указанных эффектов и в первую очередь для уменьшения уровня лепестков в полосах задержания усеченная импульсная характеристика умножается на весовую функцию, плавно спадающую к краям:
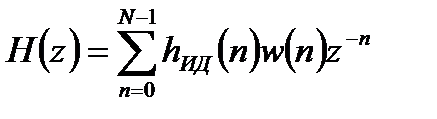 . (2.5)
. (2.5)
Платой за уменьшение уровня боковых лепестков является некоторое расширение полосы пропускания цифрового фильтра.
| Тип окна | Уровень боковых лепестков, дБ |
| прямоугольное | -13.0 |
| Треугольное (Бартлетта) | -26.5 |
| Ханна | -44.0 |
| Хэмминга | -53.6 |
| Блэкмена | -75.3 |
| Кайзера при β=4 | -45.2 |
| Кайзера при β=9 | -90.5 |
| Чебышева при β=40 дБ | -51.0 |
| Чебышева при β=60 дБ | -71.6 |
| Чебышева при β=80 дБ | -92.4 |
Дата добавления: 2017-09-19; просмотров: 1104;
