Синтез ЦФ с линейной ФЧХ

Синтез ЦФ с линейной ФЧХ основан на представлении комплексной частотной характеристики фильтра 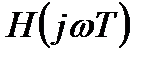в виде произведения вещественной частотной характеристики 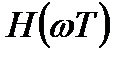и фазового множителя :

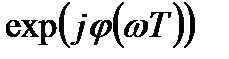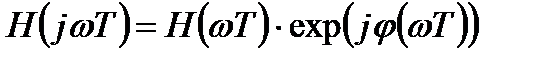. (3.16)

Вещественную частотную характеристику (ЧХ), как периодическую функцию частоты, можно представить рядом Фурье:

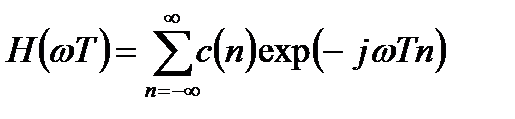, (3.17)

где .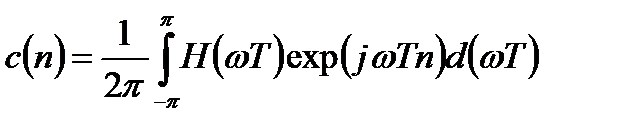

Комплексную частотную характеристику с учетом (3.17) можно представить в виде:

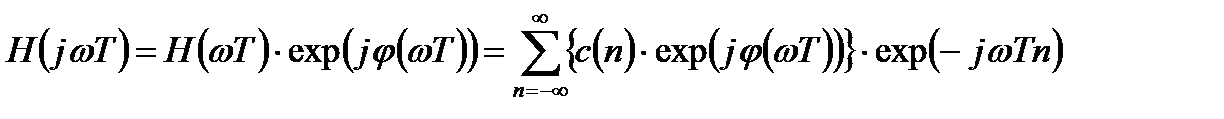. (3.18)

Учтем, что в общем случае комплексная частотная характеристика ЦФ определяется z-преобразованием от импульсной характеристики:

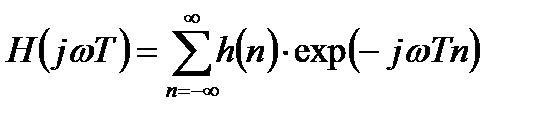. (3.19)

В соответствии с выражениями (3.19) и (3.18) импульсную характеристику ЦФ можно представить через коэффициенты 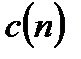ряда Фурье:

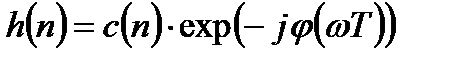. (3.20)

Ограничим импульсную характеристику конечным числом отсчетов 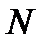и потребуем, чтобы ФЧХ фильтра являлась линейной:

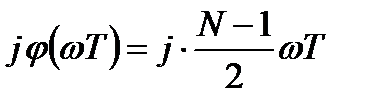. (3.21)

В этом случае импульсная характеристика ЦФ (3.20) примет вид:

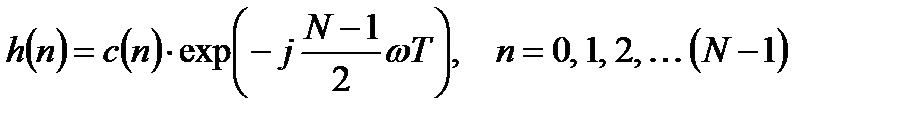. (3.22)

В операторной форме с учетом 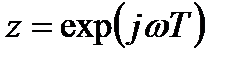выражение (3.22) запишется следующим образом:

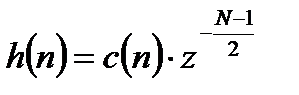. (3.23)

Множитель 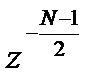можно рассматривать как оператор сдвига, смещающий последовательность коэффициентов 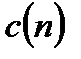в сторону положительных значений 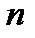на интервал :

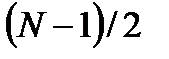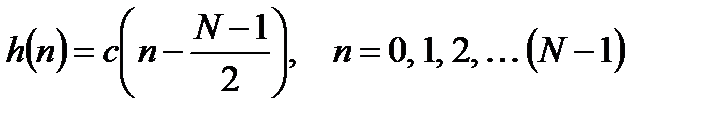. (3.24)

Таким образом, с учетом выражения (3.17) импульсную характеристику ЦФ (3.24) можно записать в виде:

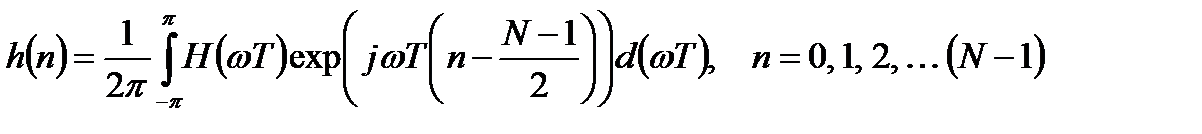. (3.25)

Для четных и нечетных функций частоты 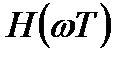выражение (3.25) с учетом 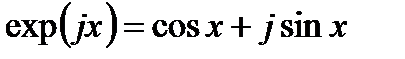конкретизируется следующим образом:

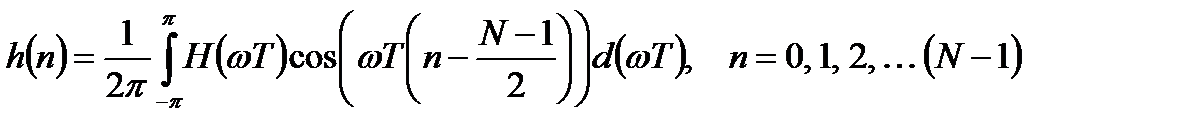; (3.26)

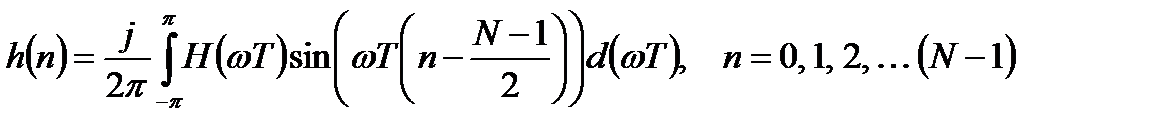. (3.27)

С учетом действительного характера импульсной характеристики комплексный множитель 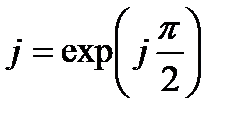в выражении (3.27) следует отнести к ФЧХ фильтра с нечетной функцией 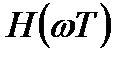, добавив к ней постоянное угловое смещение :

.

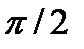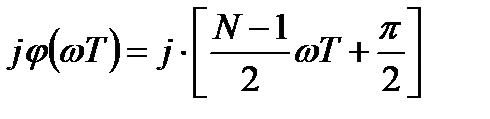В этом случае множитель 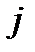в выражении (3.27) можно не учитывать. Соответственно, можно сделать вывод, что ЦФ с линейной фазой и нечетной частотной характеристикой могут использоваться для синтеза цифрового преобразования Гильберта, обеспечивающего сдвиг по фазе на 90°.