Цифровая обработка сигналов в частотной области

Рассмотренные алгоритмы дискретной линейной свертки находят широкое применение только для относительно коротких дискретных последовательностей. Для дискретных сигналов, достигающих сотен и тысяч отсчетов, возникает проблема сокращения вычислительных затрат. Сокращение вычислительных затрат достигается за счет цифровой фильтрации сигналов в частотной области и использования быстрых алгоритмов БПФ и ОБПФ.

Рисунок 2.1 – Блок-схема алгоритма обработки в частотной области

Алгоритм фильтрации в частотной области записывается следующим образом:

1. Конечная последовательность отсчетов входного сигнала 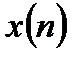и импульсная характеристика фильтра 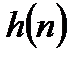дополняются нулями так, чтобы длины последовательностей стали равными.

2. Вычисляются ДПФ дополненных нулями последовательностей в виде 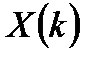и .

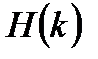3. Вычисленные ДПФ поэлементно умножаются для реализации приближенного умножения полученного спектра входного сигнала на частотную характеристику фильтра: 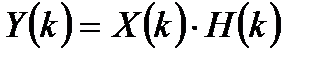(приближенная реализация, так как непрерывные спектр и частотная характеристика дискретных сигналов заменяются дискретными отсчетами ДПФ).

4. Вычисляется ОДПФ от результата перемножения: .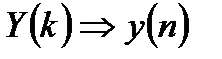

Для снижения вычислительных затрат при вычислении ДПФ входного сигнала и при обратном преобразовании во временную область целесообразно использовать алгоритмы БПФ и обратного БПФ (ОБПФ). Блок-схема алгоритма фильтрации в частотной области представлена на рисунке 2.1.

Однако в общем случае результаты фильтрации дискретного сигнала в частотной области не совпадает с дискретной линейной сверткой. Например, эти различия для цифрового фильтра в виде задержки на один временной дискрет приведены на рисунке 2.2. Различия являются следствием предположения о периодическом продолжении сигналов за пределами окна анализа при вводе понятия ДПФ.

Рисунок 2.2 – различия линейной свертки и свертки в частотной области

Круговая свертка

Пусть последовательност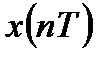и и 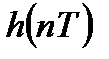являются периодическими с периодами из 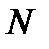отсчетов. В этом случае для них могут быть вычислены соответствующие ДПФ: 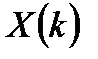и 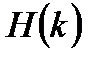. В результате перемножения ДПФ можно получить:

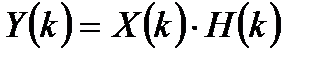. (1.8)

Результатом применения обратного дискретного преобразования Фурье (ОДПФ) к дискретному спектру 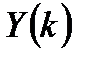является круговая свертка периодических последовательносте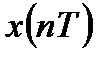й и .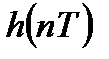

Круговая (периодическая, циклическая) свертка периодических последовательностей определяется выражениями:

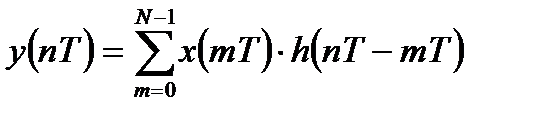(1.9)

или

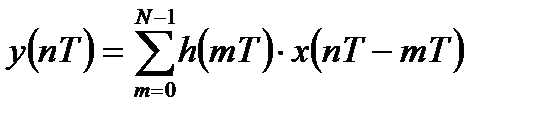. (1.10)

В случае круговой свертки выходная последовательность 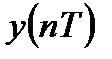также является периодической с периодом в 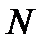отсчетов. Поэтому круговую свертку достаточно вычислять на одном периоде.

Можно показать, что результатом применения обратного дискретного преобразования Фурье (ОДПФ) к дискретному спектру 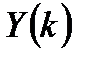является круговая свертка периодических последовательносте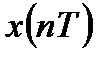й и :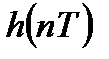

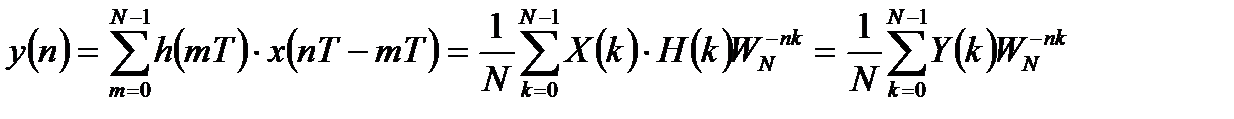. (1.11)

В матричном виде круговая свертка для N=4 имеет вид:

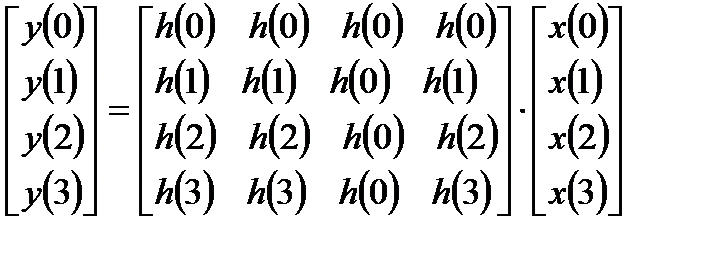. (1.12)