Производная по направлению
Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении.
Пусть задано скалярное поле, т.е. задана функция 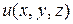 , и точка
, и точка 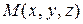 . Будем предполагать, что функция
. Будем предполагать, что функция 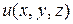 непрерывна и имеет непрерывные производные по своим аргументам в области
непрерывна и имеет непрерывные производные по своим аргументам в области 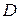 .
.
Проведем из точки 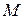 вектор
вектор 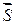 , направляющие косинусы которого
, направляющие косинусы которого 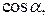
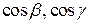 . На векторе
. На векторе 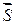 , на расстоянии
, на расстоянии 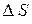 от его начала, рассмотрим точку
от его начала, рассмотрим точку 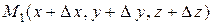 . Тогда
. Тогда 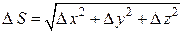 .
.
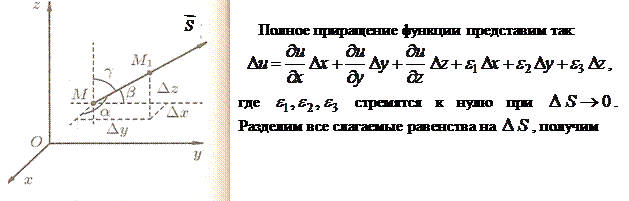
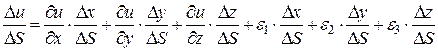 .
.
Учитывая, что 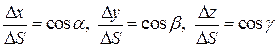 , то полученное равенство будет иметь следующий вид:
, то полученное равенство будет иметь следующий вид:
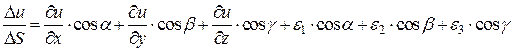 .
.
Перейдем к пределу при 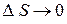 .
.
Определение 4.3. Предел отношения 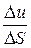 при
при 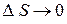 называется производной от функции
называется производной от функции 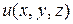 в точке
в точке 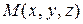 по направлению вектора
по направлению вектора 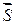 и обозначается
и обозначается 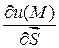 , т.е.
, т.е.
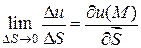 .
.
Итак, если функция 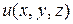 дифференцируемая, то производная от функции в точке
дифференцируемая, то производная от функции в точке 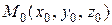 по направлению вектора
по направлению вектора 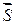 находится по следующей формуле:
находится по следующей формуле:
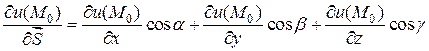 , (4.1)
, (4.1)
где 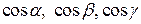 - направляющие косинусы вектора
- направляющие косинусы вектора 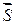 .
.
В случае функции двух переменных 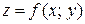 , т.е. когда поле плоское, формула (4.1) примет следующий вид:
, т.е. когда поле плоское, формула (4.1) примет следующий вид:
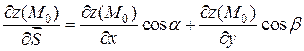 , (4.2)
, (4.2)
где 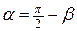 .
.
Подобно тому, как частные производные 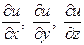 характеризуют скорость изменения функции
характеризуют скорость изменения функции 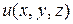 в направлении осей координат, так и производная по направлению
в направлении осей координат, так и производная по направлению 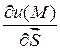 будет являться скоростью измененияфункции
будет являться скоростью измененияфункции 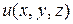 в точке
в точке 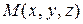 по направлению вектора
по направлению вектора 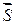 .
.
Градиент
В каждой точке области 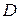 , в которой задана функция
, в которой задана функция 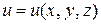 , определим вектор, проекциями которого на оси координат являются значения частных производных
, определим вектор, проекциями которого на оси координат являются значения частных производных 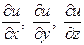 в выбранной точке
в выбранной точке 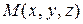 . Назовем этот вектор градиентом функции
. Назовем этот вектор градиентом функции 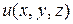 и обозначим его символами
и обозначим его символами 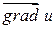 или
или 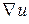 (набла-оператор, записываемый в виде «вектора» с компонентами
(набла-оператор, записываемый в виде «вектора» с компонентами 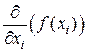 ).
).
Определение 4.4. Градиентом функции 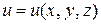 в точке
в точке 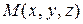 называется вектор, проекции которого служат значения частных производных этой функции, т.е.
называется вектор, проекции которого служат значения частных производных этой функции, т.е.
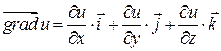 . (4.3)
. (4.3)
Подчеркнем, что проекции градиента зависят от выбора точки 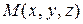 и изменяются с изменением координат этой точки. Таким образом, каждой точке скалярного поля, определяемого функцией
и изменяются с изменением координат этой точки. Таким образом, каждой точке скалярного поля, определяемого функцией 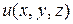 , соответствует определенный вектор – градиент этой функции. Отметим, что градиент линейной функции
, соответствует определенный вектор – градиент этой функции. Отметим, что градиент линейной функции 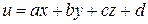 есть постоянный вектор
есть постоянный вектор 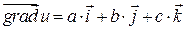 .
.
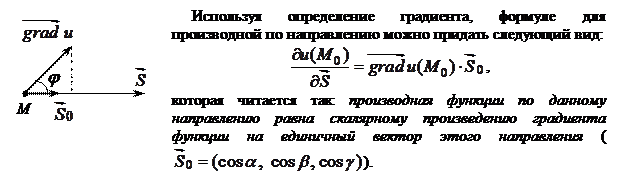
Учитывая то, что скалярное произведение равно модулю одного вектора умноженному на проекцию другого вектора на направление первого, то можно еще сказать, что: производная функции по данному направлению равна проекции градиента функции на направление дифференцирования, т.е.
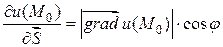 ,
,
где j - угол между 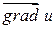 и направлением
и направлением 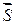 .
.
Установим некоторые свойства градиента.
Отсюда следует, что производная по направлению достигает наибольшего значения, когда 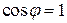 , т.е. при
, т.е. при 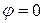 .
.
1) Производная в данной точке по направлению вектора 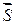 имеет наибольшее значение, если направление вектора
имеет наибольшее значение, если направление вектора 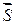 совпадает с направлением градиента; это наибольшее значение производной равно
совпадает с направлением градиента; это наибольшее значение производной равно 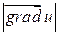 .
.
Таким образом, направление градиента есть направление наискорейшего возрастания функции. В противоположном направлении функция будет быстрее всего убывать. 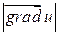 - наибольшая скорость изменения функции
- наибольшая скорость изменения функции 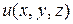 в точке
в точке 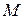 .
.
2) Производная по направлению вектора, перпендикулярного к вектору 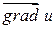 , равна нулю.
, равна нулю.
3) Градиент функции в каждой точке направлен по нормали к поверхности уровня скалярного поля, проходящего через эту точку.
Пример 4.2. Дана функция 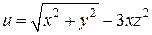 . Найти:
. Найти:
1) производную в точке 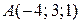 по направлению вектора
по направлению вектора 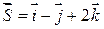 ;
;
2) производную в точке 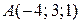 по направлению к точке
по направлению к точке 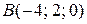 ;
;
3) градиент функции в точке 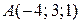 ;
;
4) наибольшую скорость возрастания функции в точке 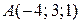 .
.
Решение. 1) Находим частные производные и значения частных производных в точке 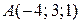 :
:
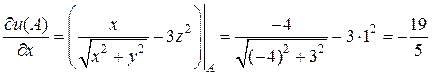 ;
;
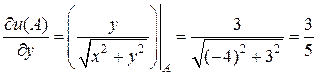 ;
;
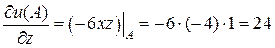 .
.
Находим направляющие косинусы вектора 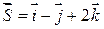 :
:
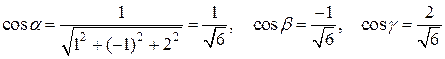 .
.
Тогда по формуле (4.1) получаем:
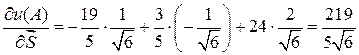 .
.
Так как 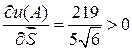 , то в данном направлении функция возрастает.
, то в данном направлении функция возрастает.
2) Находим координаты и направляющие косинусы вектора 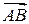 :
:
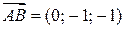 ;
;
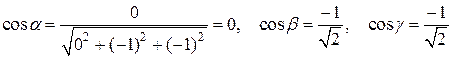 .
.
Тогда по формуле (19.16) получаем:
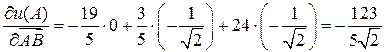 .
.
Так как 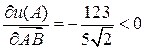 , то в данном направлении функция убывает.
, то в данном направлении функция убывает.
3) Используя формулу (4.3) запишем градиент функции в точке 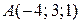 :
:
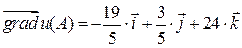 .
.
4) Находим наибольшую скорость возрастания функции в точке 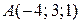 :
:
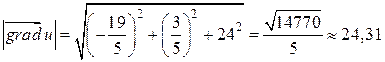 .
.
,
Дата добавления: 2017-09-19; просмотров: 5211;
