Производная сложной функции. Полная производная

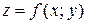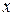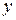Пусть - функция двух переменных и , каждая из которых является функцией независимой переменной 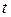, т.е. 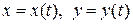. В этом случае функция 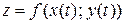является сложной функцией одной независимой переменной 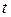, а переменные 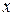и 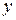будут промежуточными переменными.

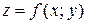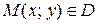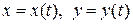Теорема 2.2. Если - функция, дифференцируемая в точке , и - дифференцируемые функции независимой переменной 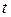, то производная сложной функции 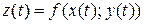вычисляется по формуле:

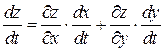. (2.9)

Доказательство. Дадим независимой переменной 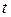приращение 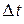. Тогда функции 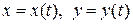получат приращения 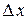и 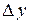соответственно. Они, в свою очередь, вызовут приращение 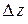функции .

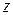Так как по условию функция 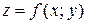дифференцируема в точке 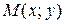, то ее полное приращение можно представить в виде

,

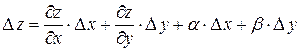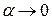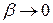где и при 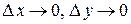. Разделим выражение 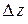на 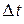и перейдем к пределу при 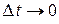. Тогда 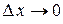и 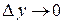в силу непрерывности функций 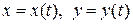(по условию они дифференцируемые). Получаем:

.

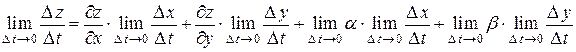Далее

,

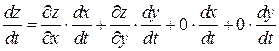или

. ,

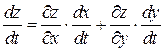Частный случай: 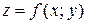, где 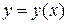, т.е. 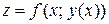- сложная функция одной независимой переменной 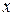. Этот случай сводится к предыдущему, причем роль переменной 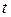играет 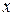. Согласно формуле (2.9) имеем:

,

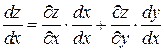или

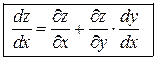. (2.10)

Формула (2.10) называется формулой полной производной.

Общий случай: 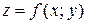, где 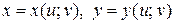. Тогда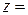 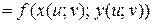- сложная функция независимых переменных 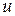и 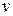. Ее частные производные 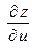и 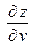можно найти по следующим формулам:

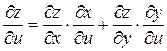и 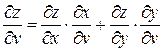. (2.11)

Пример 2.7. Найти 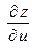, если .

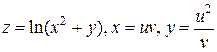Решение. Используя формулу (2.11), найдем :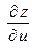

,

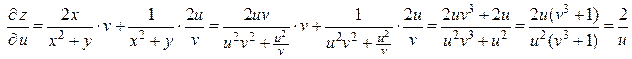Надо отметить, что формулы (2.11) можно обобщить для случая большего числа переменных.

Используя правило дифференцирования сложной функции, можно показать, что полный дифференциал обладает свойством инвариантности: полный дифференциал функции 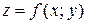сохраняет один и тот же вид независимо от того, является ли аргументы независимыми переменными или функциями независимых переменных.