Экстремум функции двух переменных

Понятие максимум, минимум, экстремум функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной. Пусть функция 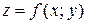определена в некоторой области 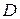, точка .

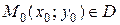Определение 3.4. Точка 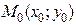называется точкой максимума 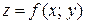, если существует такая 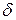-окрестность точки 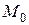, что для каждой точки 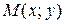, отличной от 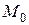, из этой окрестности выполняется неравенство

.

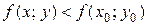Определение 3.5. Точка 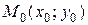называется точкой минимума 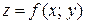, если существует такая 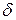-окрестность точки 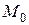, что для каждой точки 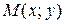, отличной от 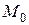, из этой окрестности выполняется неравенство

.

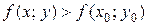Значение функции в точке максимум (минимум) называется максимум (минимум) функции. Максимум и минимум функции называют ее экстремумами.

Отметим, что, в силу определения, точка экстремума лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер; значение функции в точке 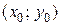сравнивается с ее значениями в точках, достаточно близких к 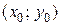. В области 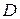функция может иметь несколько экстремумов или не иметь ни одного.

Рассмотрим условия существования экстремума функции.