В замкнутой области
1. Найти все критические точки функции, принадлежащие 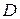 , и вычислить значения функции в них.
, и вычислить значения функции в них.
2. Найти наибольшее и наименьшее значения функции 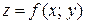 на границах области.
на границах области.
3. Сравнить все найденные значения функции и выбрать из них наибольшее 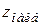 и наименьшее
и наименьшее 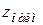 .
.
Пример 3.3. Найти наибольшее и наименьшее значения функции 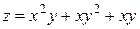 в замкнутой области
в замкнутой области 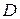 , ограниченной линиями:
, ограниченной линиями: 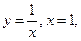
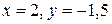 .
.
Решение. 1) Строим замкнутую область  , ограниченную линиями:
, ограниченную линиями: 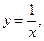
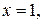
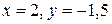 .
.
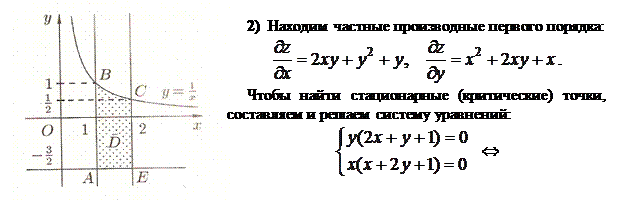
Û 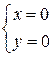 ,
, 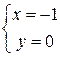 ,
, 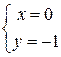 ,
, 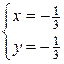 .
.
Таким образом, получаем четыре стационарные точки, ни одна из которых не принадлежит области 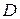 .
.
3) Исследуем функцию на границе области, состоящей из участков 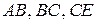 и
и 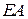 .
.
а) на границу 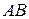 :
: 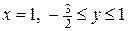 .
.
Тогда получаем функцию от одной переменной 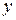 :
: 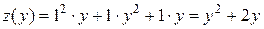 . Находим критические точки:
. Находим критические точки: 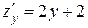 .
.
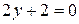 Þ
Þ 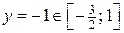 .
.
Далее 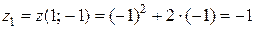 .
.
б) на границу 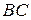 :
: 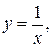
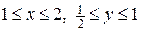 .
.
Тогда получаем функцию от одной переменной 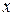 :
: 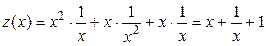 . Находим критические точки:
. Находим критические точки: 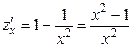 .
.
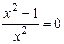 Þ
Þ 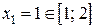 и
и 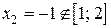 .
.
Далее 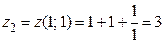 .
.
в) на границу 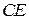 :
: 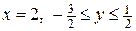 .
.
Тогда получаем функцию от одной переменной 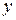 :
: 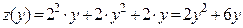 . Находим критические точки:
. Находим критические точки: 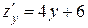 .
.
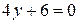 Þ
Þ 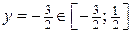 .
.
Далее 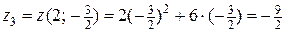 .
.
г) на границу 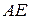 :
: 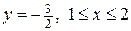 .
.
Тогда получаем функцию от одной переменной 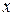 :
:
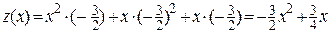 .
.
Находим критические точки: 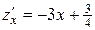 .
.
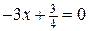 Þ
Þ 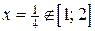 . Значит, на границе
. Значит, на границе 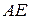 критических точек нет.
критических точек нет.
4) Находим значения функции в вершинах области: 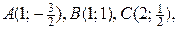
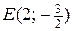 . Выше были найдены значения функции
. Выше были найдены значения функции 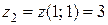 и
и 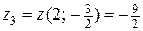 , что соответствует значениям функции в точках
, что соответствует значениям функции в точках 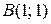 и
и 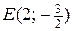 . Поэтому находим значения функции в точках
. Поэтому находим значения функции в точках 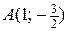 и
и 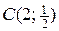 :
:
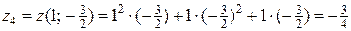 ;
;
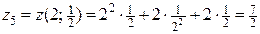 .
.
Из всех полученных значений функции 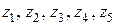 выбираем наибольшее и наименьшее:
выбираем наибольшее и наименьшее:
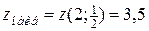 ;
; 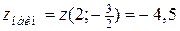 .
.
,
3. ОСНОВНЫЕ ПОНЯТИЯ СКАЛЯРНОГО ПОЛЯ
Скалярное поле
Предположим, что в каждой точке 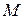 некоторой области
некоторой области 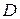 задано значение скалярной физической величины
задано значение скалярной физической величины 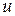 , т.е. такой величины, которая полностью характеризуется своим числовым значением. Например, это может быть температура точек неравномерно нагретого тела, плотность распределения электрических зарядов в изолированном наэлектризованном теле, потенциал электрического поля и т.д. При этом
, т.е. такой величины, которая полностью характеризуется своим числовым значением. Например, это может быть температура точек неравномерно нагретого тела, плотность распределения электрических зарядов в изолированном наэлектризованном теле, потенциал электрического поля и т.д. При этом 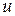 называется скалярной функцией точки, записывается это так
называется скалярной функцией точки, записывается это так 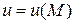 . Область
. Область 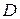 , в которой определена функция
, в которой определена функция 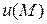 , может совпадать со всем пространством, а может являться некоторой его частью.
, может совпадать со всем пространством, а может являться некоторой его частью.
Определение 4.1. Если в области 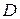 задана скалярная функция точки
задана скалярная функция точки 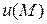 , то говорят, что в этой области задано скалярное поле.
, то говорят, что в этой области задано скалярное поле.
Будем считать, что скалярное поле стационарное, т.е. величина 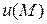 не зависит от времени
не зависит от времени 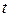 .
.
Если физическая величина векторная, то ей будет соответствовать векторное поле, например, силовое поле, электрическое поле напряженности, магнитное поле и др.
Если скалярное поле отнесено к системе координат 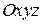 , то задание точки
, то задание точки 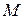 равносильно заданию ее координат
равносильно заданию ее координат 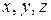 , и тогда функция
, и тогда функция 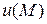 можно записать в обычном виде функции трех переменных:
можно записать в обычном виде функции трех переменных: 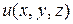 .
.
Рассмотрим точки области 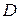 , в которых функция
, в которых функция 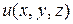 имеет постоянное значение
имеет постоянное значение 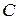 , т.е.
, т.е. 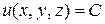 . Совокупность этих точек образует некоторую поверхность. Если возьмем другое значение
. Совокупность этих точек образует некоторую поверхность. Если возьмем другое значение 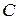 , то получим другую поверхность. Эти поверхности называются поверхностями уровня.
, то получим другую поверхность. Эти поверхности называются поверхностями уровня.
Определение 4.2. Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция 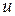 принимает постоянное значение, т.е.
принимает постоянное значение, т.е.
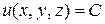 .
.
В курсе физики при рассмотрении поля потенциала поверхности уровня называют обычно эквипотенциальными поверхностями (т.е. поверхности равного потенциала).
Если скалярное поле плоское, т.е. изучается распределение значений величины в какой-то плоской области, то функция 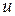 зависит от двух переменных, например,
зависит от двух переменных, например, 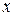 и
и 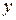 . Линиями уровня этого поля будут линии уровня функции
. Линиями уровня этого поля будут линии уровня функции 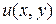 , т.е.
, т.е. 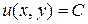 .
.
В прикладных науках часто употребляются линии уровня для представления изучаемой функции двух независимых переменных. Так, например, рассматривая высоту точки местности над уровнем моря как функцию двух переменных – координат точки, на карты наносят линии уровня этой функции. Они называются в топологии горизонталями. С помощью сети горизонталей удобно следить за изменением высоты местности. В метеорологии пользуются сетями изотерм и изобар (линий одинаковых средних температур и линий равных средних давлений), являющимися линиями уровня температуры и давления как функции координат точки местности.
Пример 4.1. Построить в плоскости 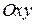 линии уровня функции
линии уровня функции 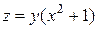 .
.
Дата добавления: 2017-09-19; просмотров: 842;
