Дифференцируемость и полный дифференциал функции

Пусть функция 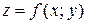определена в некоторой окрестности точки 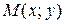. Составим полное приращение функции в точке :

.

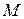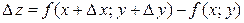Определение 2.3. Функция 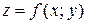называется дифференцируемой в точке 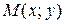, если ее полное приращение в этой точке можно представить в виде

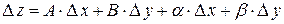, (2.3)

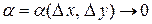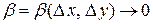где и при .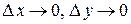

Сумма первых двух слагаемых в равенстве (2.3) представляет собой главную часть приращения функции.

Определение 2.4. Главная часть приращения функции 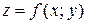, линейная относительно 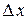и 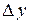, называется полным дифференциалом этой функции и обозначается символом :

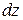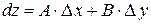. (2.4)

Выражения 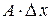и 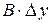называются частными дифференциалами. Для независимых переменных 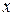и 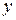полагают 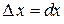и 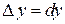. Поэтому равенство (2.4) можно представить в виде

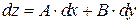. (2.5)

Надо отметить, если функция 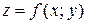дифференцируема в точке 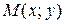, то она непрерывна в этой точке, имеет в ней частные производные 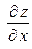и 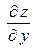, причем 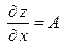, 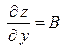. Тогда формула для вычисления полного дифференциала примет вид:

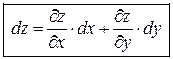. (2.6)

Для функции 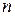переменных 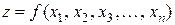полный дифференциал определяется выражением

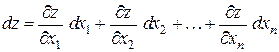. (2.7)

Пример 2.5. Найти полный дифференциал функции .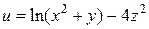

Решение. Находим частные производные первого порядка:

, , .

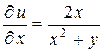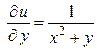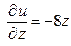Согласно формуле (2.7) получаем

.

,

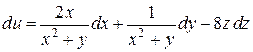Полный дифференциал функции (формула (2.6)) называется также дифференциалом первого порядка.

Введем понятие дифференциала высшего порядка. Пусть функция 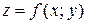имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле 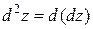. Найдем его:

.

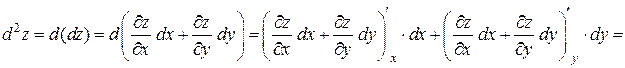
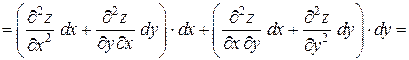
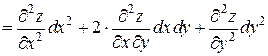Итак,

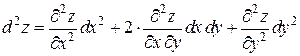. (2.8)

Аналогично можно получить формулы для дифференциала третьего и более высокого порядков.

Пример 2.6. Найти 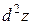, если .

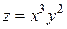Решение. Находим частные производные первого порядка:

.

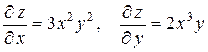Находим частные производные второго порядка:

, , .

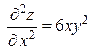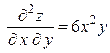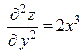Согласно формуле (2.8) получаем

.

,