Возрастание и убывание функции. Точки экстремума
Говорят, что функция 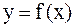 возрастает (убывает) на интервале
возрастает (убывает) на интервале 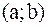 , если для любых различных точек
, если для любых различных точек 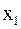 ,
, 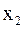 из
из 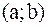 справедливо неравенство
справедливо неравенство 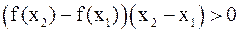
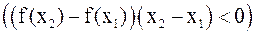 , т.е. если большему значению аргумента соответствует большее (меньшее) значение функции.
, т.е. если большему значению аргумента соответствует большее (меньшее) значение функции.
Теорема 1. Если функция f(x) дифференцируема на (a; b) и 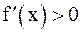 (
( 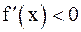 ) для любого
) для любого 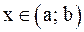 , то f(x) возрастает (убывает) на (a, b).
, то f(x) возрастает (убывает) на (a, b).
Точка x0 называется точкой максимума (минимума) функции f(x), определённой в некоторой окрестности x0, если существует некоторая окрестность (x0 – d; x0 + d) этой точки, такая что для любого xÎ(x0 – d; x0 + d), x ¹ x0 справедливо неравенство f(x) < f(x0) (f(x) > f(x0)); при этом f(x0) называют максимумом (минимумом) функции. Точки максимума и точки минимума называют точками экстремума.
Теорема 2 (необходимое условие экстремума). Если функция f(x) дифференцируема в промежутке (a,b) и x0Î(a, b) является точкой экстремума f(x), то 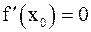 .
.
Точки, в которых 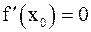 , называются стационарными точками f(x). Не всякая стационарная точка является точкой экстремума.
, называются стационарными точками f(x). Не всякая стационарная точка является точкой экстремума.
Теорема 3 (достаточное условие экстремума). Пусть функция f(x) дифференцируема в окрестности стационарной точки x0. Если при переходе через точку x0 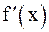 меняет свой знак, то x0 является точкой экстремума. А именно, если при переходе через точку x0
меняет свой знак, то x0 является точкой экстремума. А именно, если при переходе через точку x0 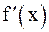 :
:
а) меняет свой знак с минуса на плюс (то есть 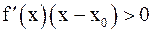 при достаточно малых значениях
при достаточно малых значениях 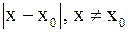 ), то x0 является точкой минимума;
), то x0 является точкой минимума;
б) меняет свой знак с плюса на минус (то есть 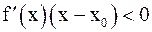 при достаточно малых значениях
при достаточно малых значениях 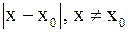 ), то x0 является точкой максимума функции;
), то x0 является точкой максимума функции;
в) не меняет своего знака, то x0 не является точкой экстремума.
Иногда удобно пользоваться другим достаточным условием экстремума.
Теорема 4 (достаточное условие экстремума). Пусть x0 – стационарная точка функции f(x), дважды дифференцируемой в точке x0. Если 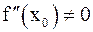 , то x0 является точкой экстремума. Точнее говоря, если: а)
, то x0 является точкой экстремума. Точнее говоря, если: а) 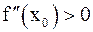 , то x0 – точка минимума; б)
, то x0 – точка минимума; б) 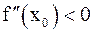 , то x0 – точка максимума.
, то x0 – точка максимума.
Точкой экстремума f(x) может оказаться и точка, в которой 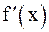 не определена. Стационарные точки и точки, в которых
не определена. Стационарные точки и точки, в которых 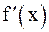 не определена, называют критическими точками функции.
не определена, называют критическими точками функции.
Пример 1. Найти точки экстремума функции 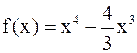 .
.
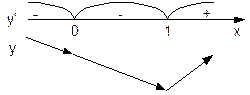 Решение. Наша функция дифференцируема на всей числовой оси. Найдём стационарные точки.
Решение. Наша функция дифференцируема на всей числовой оси. Найдём стационарные точки. 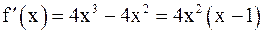 . Стационарными точками являются
. Стационарными точками являются 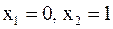 . При переходе через точку
. При переходе через точку 
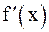 не меняет своего знака, поэтому эта точка не является точкой экстремума. При переходе через точку
не меняет своего знака, поэтому эта точка не является точкой экстремума. При переходе через точку 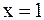
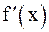 меняет свой знак с «–» на «+», следовательно,
меняет свой знак с «–» на «+», следовательно, 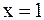 – точка минимума (на рисунке получается «впадина»).
– точка минимума (на рисунке получается «впадина»).
Для нахождения наибольшего и наименьшего значений функции на отрезке 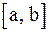 находят значения функции в критических точках, принадлежащих этому отрезку, и на концах отрезка, после чего сравнивают эти значения и выбирают наибольшее и наименьшее.
находят значения функции в критических точках, принадлежащих этому отрезку, и на концах отрезка, после чего сравнивают эти значения и выбирают наибольшее и наименьшее.
Пример 2. Найти наибольшее и наименьшее значения функции 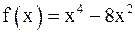 на отрезке [–1; 3].
на отрезке [–1; 3].
Решение.Функция дифференцируема на всей числовой оси. Найдём стационарные точки
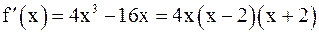 .
.
Стационарными точками являются x1 = –2, x2 = 0, x3 = 2; из них лишь x2 = 0 и x3 = 2 принадлежат промежутку [–1; 3] . Найдём значения функции в точках x = 0, x = 2, а также на концах отрезка: f(0) = 0,
f(2) =16 – 32 = –16, f(–1) = 1 – 8 = –7, f(3) = 81 – 72 = 9. Сравнив полученные значения, находим:
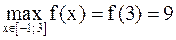 ,
, 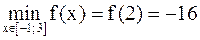 .
.
Дата добавления: 2019-07-26; просмотров: 777;
