Выпуклость и вогнутость

Дифференцируемая функция 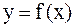называется выпуклой (вогнутой) или выпуклой вверх (вниз) на интервале (a; b), если она удовлетворяет следующему условию: для любых различных точек x₁, x₂Î(a;b) часть графика функции y = f(x), соответствующая интервалу (x₁; x₂), расположена выше (ниже) отрезка M₁M₂, где M₁(x₁; f(x₁)), M₂(x₂; f(x₂)).

Точка графика функции, разделяющая выпуклый и вогнутый участки графика, называется точкой перегиба (часто точкой перегиба называют абсциссу этой точки графика функции).

Теорема 5.Если для функции f(x), дважды дифференцируемой в (a; b), 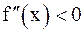( 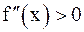) при всех xÎ(a; b), то функция f(x) является выпуклой (вогнутой) на (a; b) .

Теорема 6. Пусть функция f(x) дважды дифференцируема на (a; b). Точка x₀Î(a; b) является точкой перегиба в том и только в том случае, если одновременно выполняются два условия: 1) 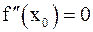; 2) при переходе через точку x₀ 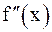меняет свой знак.

В последней теореме при условии трижды дифференцируемости функции условие 2) можно заменить на .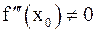

Асимптоты

Прямая (L) называется асимптотой графика функции (или просто асимптотой функции), если расстояние d(M; (L)) от точки М на графике функции y = f(x) до прямой (L) стремится к 0 при неограниченном удалении точки М от начала координат.

Различают два вида асимптот: вертикальные и наклонные.

Прямая x = x₀ является вертикальной асимптотой, если по крайней мере один из односторонних пределов f(x₀ – 0), f(x₀ + 0) равен –¥ или +¥.

Наклонная асимптота y = kx + b соответствует случаю x® – ¥ или x® + ¥. Коэффициенты k и b при x® + ¥ находятся из равенств

,

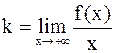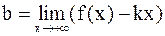
(то же при x® – ¥). Если же не существует одного из пределов или один из этих пределов равен – ¥ или + ¥, то у функции отсутствует наклонная асимптота при x® + ¥ (то же при x® – ¥).