Производная обратных функций
Пусть требуется найти производную функции у = f(x)при условии, что обратная ей функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.
Для решения этой задачи дифференцируем функцию x = g(y) по х:
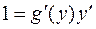 , т.к. g¢(y) ¹ 0 , то
, т.к. g¢(y) ¹ 0 , то 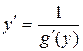 ,
, 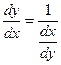 т.е. производная обратной функции обратна по величине производной данной функции.
т.е. производная обратной функции обратна по величине производной данной функции.
Теорема.Если функция y=f(x) строго монотонна на интервале (a; b) и имеет неравную нулю производную 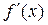 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция 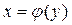 также имеет производную
также имеет производную 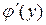 в соответствующей точке, определяемую равенством
в соответствующей точке, определяемую равенством 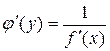 или
или 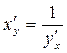 .
.
Пример 6. Найти формулу для производной функции arctg(х).
Решение.Функция arctg является функцией, обратной функции tg, т.е. ее производная может быть найдена следующим образом: 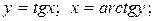 Известно, что
Известно, что 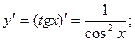 По приведенной выше формуле получаем:
По приведенной выше формуле получаем: 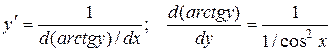 . Т.к.
. Т.к. 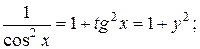 то можно записать окончательную формулу для производной арктангенса:
то можно записать окончательную формулу для производной арктангенса: 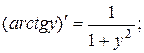
Пример 7. Пользуясь правилом дифференцирования обратной функции, найти производную 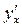 для функции
для функции 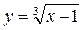 .
.
Решение.Обратная функция: 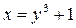 , отсюда
, отсюда 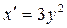 .Тогда
.Тогда 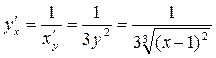 .
.
Дата добавления: 2017-12-05; просмотров: 1345;
