Касательная плоскость и нормаль к плоскости кривой. Угол между двумя кривыми
Если плоская кривая задана функцией 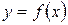 , то уравнения касательной и нормали в точке
, то уравнения касательной и нормали в точке 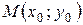 имеют вид:
имеют вид:
Уравнение касательной к кривой: 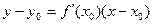 .
.
Уравнение нормали к кривой: 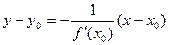 .
.
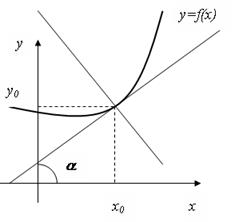
Рис. 13
Замечание: направление кривой в каждой ее точке определяется направлением касательной в этой точке.
|
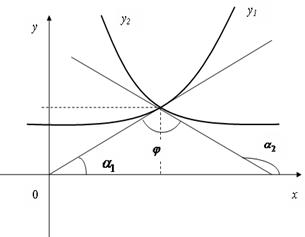
| Рис.14 |
Угол между пересекающими кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (Рис. 14) по формуле 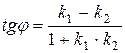 , где
, где 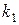 и
и 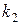 - угловые коэффициенты касательных к кривым в точке их пересечения
- угловые коэффициенты касательных к кривым в точке их пересечения 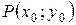 , т.е. частные значения в точке
, т.е. частные значения в точке 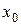 производных от y по x из уравнений этих
производных от y по x из уравнений этих
кривых: 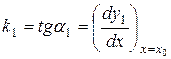 ,
, 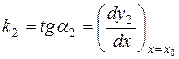 .
.
Пример 6.Найти уравнения касательной и нормали к кривой в заданной точке:
а) 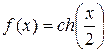 при
при 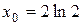 .
.
Решение.Из уравнения кривой найдем 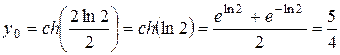 и производную
и производную 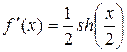
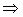
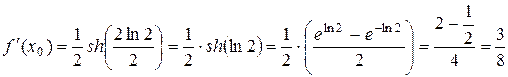 .
.
Уравнение касательной: 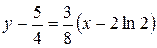
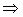
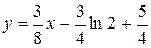 .
.
Уравнение нормали: 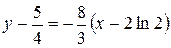
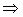
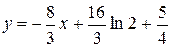 .
.
б) 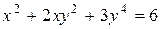 в точке
в точке 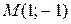 .
.
Решение.Из уравнения кривой найдём производную: 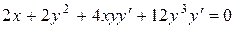 , т.е.
, т.е. 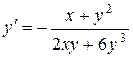 .
.
Следовательно, 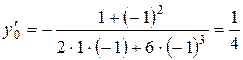 .
.
Уравнение касательной: 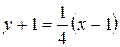 или
или 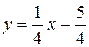 .
.
Уравнение нормали: 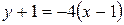 или
или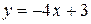 .
.
в) 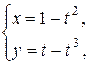 при
при 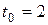 .
.
Решение.Найдём 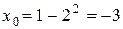 ,
, 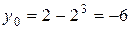 и
и 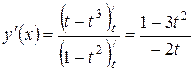 . Следовательно
. Следовательно 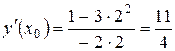 .
.
Уравнение касательной: 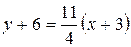 или
или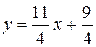 .
.
Уравнение нормали: 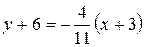 или
или 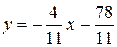 .
.
Пример 7.Найти угол между параболами 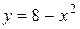 и
и 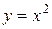 .
.
Решение.Решив совместно уравнения парабол, находим точки их пересечения 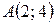 и
и 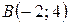 . Продифференцируем уравнения парабол:
. Продифференцируем уравнения парабол: 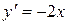 ,
, 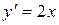 . Найдём угловые коэффициенты касательных к параболам в точке А (т.е. значения производных при х=2):
. Найдём угловые коэффициенты касательных к параболам в точке А (т.е. значения производных при х=2): 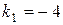 ,
, 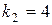 . Следовательно,
. Следовательно, 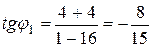 ,
, 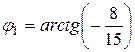 . Так же определяется угол между кривыми в точке В:
. Так же определяется угол между кривыми в точке В: 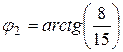 .
.
Дата добавления: 2017-12-05; просмотров: 2528;
