Формулы для вычисления кривизны линии
Таблица 5.
при 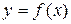
| при 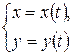
| при 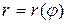
|
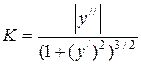
| 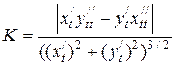
| 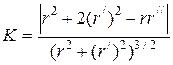
|
Радиусом кривизны называется величина, обратная кривизне: 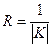 .
.
Пример 9. Найти кривизну линии 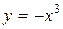 в точке с абсциссой
в точке с абсциссой 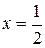 .
.
Решение. Найдем 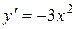 ,
, 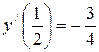 ,
, 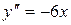 ,
, 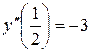 .
.
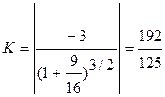 .
.
Окружностью кривизны данной линии в ее точке А называется предельное положение окружности, проходящей через три точки 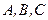 кривой, когда
кривой, когда 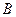
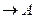 и
и 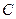
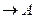 . Радиус окружности кривизны равен радиусу кривизны.
. Радиус окружности кривизны равен радиусу кривизны.
Центр окружности кривизны называется центром кривизны и находится на нормали к линии, проведенной в точке А в сторону вогнутости этой линии.
Координаты  и
и 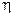 центра кривизны линии
центра кривизны линии 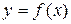 вычисляются по формулам:
вычисляются по формулам: 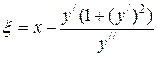 ,
, 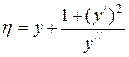 .
.
Эволютой линии называется множество ее центров кривизны.
Пример 10.Составить уравнение эволюты параболы 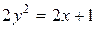 .
.
Решение. Продифференцируем 2 раза: 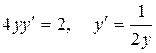 Þ
Þ 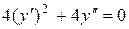 Þ
Þ 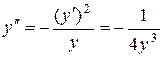 . Определяем координаты центра кривизны:
. Определяем координаты центра кривизны:
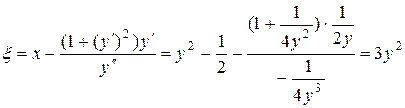 ,
, 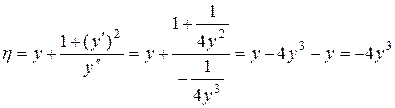 .
.
Получаем уравнение эволюты в параметрической форме: 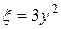 ,
, 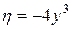 .
.
Исключив параметр у, получим уравнение эволюты: 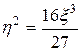 .
.
Функции нескольких переменных
Основные понятия функции нескольких переменных. Способы задания функции
При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т.к. все полученные результаты будут справедливы для функций произвольного числа переменных.
Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому - либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных. Обозначается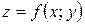 .
.
Если паре чисел (х, у) соответствует одно значение z, то функция называется однозначной, а если более одного, то – многозначной.
Как и функции одной переменной, функции двух переменных могут быть заданы таблицей (для некоторого количества пар значений независимых переменных указываются соответствующие им значения функции), аналитически (задаётся формула, при помощи которой по заданным значениям независимых переменных отыскиваются значения функции) и графиком (множество точек плоскости, абсциссы и ординаты которых являются значениями х и у, а аппликаты- соответствующие значения z). Графиком функции непрерывных аргументов служит некоторая поверхность.
Областью определения функции z называется совокупность пар (х, у), при которых функция z существует.
Пример 1. Найти область определения функции:
а) 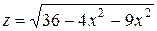
Решение.Функция z принимает действительные значения при условии 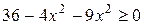 т.е.
т.е. 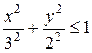 . Областью определения данной функции является эллипс с центром в начале координат (а=3 и в=2 - длины полуосей), включая граничный эллипс.
. Областью определения данной функции является эллипс с центром в начале координат (а=3 и в=2 - длины полуосей), включая граничный эллипс.
б) 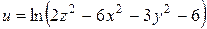
Решение. Данная функция принимает действительные значения при  т.е.
т.е. 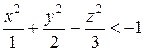 . Областью определения функции является часть пространства, заключённая внутри плоскостей двуполостного гиперболоида.
. Областью определения функции является часть пространства, заключённая внутри плоскостей двуполостного гиперболоида.
Пример 2. Найти область определения и множество значений таблично заданной функции:
Стоимость автомобиляz (тыс .руб) в зависимости от количества покупаемых автомобилей x икомплектации y
| количество автомобилей в партии | комплектация автомобиля | ||
| I | II | III | |
| 1-3 | 10,5 | ||
| 4-7 | 9,7 | 10,1 | 10,5 |
| 8-15 | 9,6 | 10,3 | |
| Более 15 | 9,5 | 9,8 | 10,2 |
Решение. 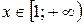 ,
, 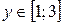 ,
,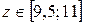 .
.
Окрестностью точкиМ0(х0, у0) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию 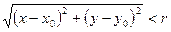 .
.
Пусть каждой точке М из множества точек 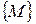 евклидового пространства
евклидового пространства 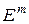 по какому-либо закону ставится в соответствие некоторое число и из числового множества U. Тогда будем говорить, что на множестве
по какому-либо закону ставится в соответствие некоторое число и из числового множества U. Тогда будем говорить, что на множестве 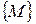 задана функция
задана функция 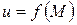 . При этом множество
. При этом множество 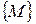 называется областью определения, U – областью изменения функции
называется областью определения, U – областью изменения функции 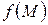 .
.
Дата добавления: 2017-12-05; просмотров: 2027;
